YOMEDIA
NONE
  • Câu hỏi:

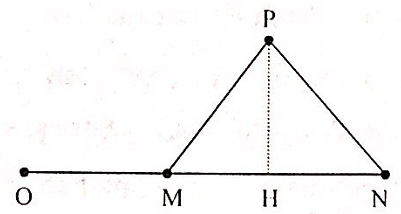
    Cho 4 điểm O, M, N và P nằm trong một môi trường truyền âm. Trong đó, M và N nằm trên nửa đường thẳng xuất phát từ O, tam giác MNP là tam giác đều. Tại O, đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại M và N lần lượt là 50 dB và 40 dB. Mức cường độ âm tại P là:

    • A. 35,8 dB
    • B. 38,8 dB
    • C. 43,6 dB 
    • D. 41,1 dB

    Lời giải tham khảo:

    Đáp án đúng: D

    + Ta có:

    \({L_M} - {L_N} = 10\lg {\left( {\frac{{ON}}{{OM}}} \right)^2} \Rightarrow 50 - 40 = 10\lg {\left( {\frac{{ON}}{{OM}}} \right)^2} \Rightarrow \frac{{ON}}{{OM}} = {10^{1/2}}\) 

    + Gọi a là cạnh tam giác đều, ta có: MN = NP = MP = a =>  

     \(\begin{array}{l}
    \frac{{OM + a}}{{OM}} = \sqrt {10} \\
     \Leftrightarrow 1 + \frac{a}{{OM}} = \sqrt {10}  \Rightarrow OM = \frac{a}{{\sqrt {10}  - 1}} \Rightarrow {L_P} = {L_M} + 10\lg {\left( {\frac{{OM}}{{OP}}} \right)^2}\\
    {L_P} - {L_M} = 10\lg {\left( {\frac{{OM}}{{OP}}} \right)^2} \Rightarrow {L_P} = 50 + 10\lg {\left( {\frac{{OM}}{{OP}}} \right)^2}
    \end{array}\)

    + Trong tam giác đều PMN ta có:  

    \(\begin{array}{l}
    \left\{ \begin{array}{l}
    PH = \frac{{a\sqrt 3 }}{2}\\
    MH = \frac{a}{2}
    \end{array} \right. \Rightarrow OP = \sqrt {O{H^2} + P{H^2}}  = 1,295a\\
     \Rightarrow \frac{{OM}}{{OP}} = \frac{1}{{1,295\left( {\sqrt {10}  - 1} \right)}}\\
     \Rightarrow {L_P} = 50 + 10\lg {\left( {\frac{1}{{1,295\left( {\sqrt {10}  - 1} \right)}}} \right)^2} = 41,1{\rm{ dB}}
    \end{array}\)

    ADSENSE

Mã câu hỏi: 208631

Loại bài: Bài tập

Chủ đề :

Môn học: Vật lý

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài

 
YOMEDIA

Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng

 

 

CÂU HỎI KHÁC

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 12

 

YOMEDIA
AANETWORK
OFF