Hôm nay chúng ta học bài 3 của chuyên đề 3: Công suất của dòng điện xoay chiều, đây là bài rất quan trọng.

Ta có: \(\left\{\begin{matrix} u = U_0\cos (\omega t + \varphi _u)\\ i = I_0 \cos (\omega t + \varphi _i) \end{matrix}\right., \ \varphi = \varphi _u - \varphi _i\)
Công suất: \(P = u.i=U_0I_0\cos (\omega t + \varphi _u).\cos (\omega t + \varphi _i)\)
\(P =\frac{ U_0I_0}{2}\left [\cos (2\omega t + \varphi _u + \varphi _i) \right ] + \cos (\underbrace{ \varphi _u - \varphi _i }_{\varphi })\)
\(P =\frac{ U_0I_0}{2}\cos \varphi + \frac{ U_0I_0}{2}\cos (2\omega t + \varphi _u + \varphi _i)\)
Công suất trung bình cộng trong 1 chu kỳ:
\(\overline{P} =\overline{\frac{ U_0I_0}{2}\cos \varphi} + \underbrace{ \overline{\frac{ U_0I_0}{2}\cos (2\omega t + \varphi _u + \varphi _i)} }_{=0}\)
\(\overline{P} =\frac{ U_0I_0}{2}\cos \varphi = UI\cos \varphi\)
Vậy công suất của dòng điện xoay chiều là công suất tính trong thời gian dài hay công suất tính trong 1 chu kỳ: \(P =\frac{ U_0I_0}{2}\cos \varphi = UI\cos \varphi\)
* Hệ số công suất

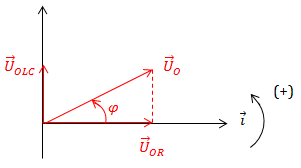
\(\cos \varphi = \frac{U_{0R}}{U_0} = \frac{U_{R}}{U} = \frac{R}{Z} = \frac{R}{\sqrt{R^2+(Z_L - Z_C)^2}}\)
Mà \(-\frac{\pi }{2} \leq \varphi \frac{\pi }{2} \Rightarrow 0\leq \cos \varphi \leq 1\)

* Ý nghĩa của hệ số công suất
+ \(\cos \varphi = 0 \Rightarrow \varphi = \pm \frac{\pi}{2}\): Mạch chỉ chứa L hoặc C hoặc LC ⇒ P = 0
+ \(\cos \varphi = 1 \Rightarrow \varphi = 0\): Mạch chỉ chứa R hoặc RLC đang xảy ra cộng hưởng điện
\(\Rightarrow P_{max} = UI_{max} = \frac{U^2}{R}\)
+ \(0 < \cos \varphi < 1 \Rightarrow \bigg \lbrack \begin{matrix} -\frac{\pi}{2}< \varphi < 0\\ 0 < \varphi < \frac{\pi}{2} \end{matrix}\): Mạch chỉ chứa RC hoặc RL hoặc cả RLC không xảy ra cộng hưởng điện
\(\Rightarrow P = UI\cos \varphi < P_{max}\)
* Thực tế: Khi sản xuất các thiết bị hoặc dụng cụ thiêu thụ điện thì hệ số công suất cos \(\varphi\) phải lớn: \(\cos \varphi\geq 0,85\)