Phương pháp giải dạng bài tập về dao động của vật rắn môn Vật Lý 10 năm 2021-2022

Cách 1. Phương pháp năng lượng

Giải theo cách 1 thì phải chọn gốc thế năng cho phù hợp (thường sử dụng cho các bài toán có hệ lực phức tạp)

Cách 2. Phương pháp động lực học

Giải theo cách 2 thì phải phân tích lực và chọn một trục quay (thường sử dụng cho các bài toán có hệ lực đơn giản).

Ví dụ 1.  Cho cơ hệ như hình vẽ, quả cầu đặc có khối lượng m, bán kính r lăn không trượt trong máng có bán kính R. Máng đứng yên trên mặt phẳng nằm ngang. Tìm chu kì dao động nhỏ của quả cầu. Cho biết momen quán tính của quả cầu đặc \({{I}_{G}}=\frac{2}{5}m{{r}^{2}}\).

Hướng dẫn

Chọn gốc thế năng hấp dẫn tại tâm O của máng cong.

Quả cầu lăn không trượt nên K là tâm quay tức thời.

Cơ năng của quả cầu tại li độ góc α.

Phương pháp năng lượng.

\(W=-mg(R-r)\cos \alpha +{{I}_{K}}\frac{\omega _{K}^{2}}{2}=const(*)\)

Với: \(\left\{ \begin{align} & {{I}_{K}}=\frac{2}{5}m{{r}^{2}}+m{{r}^{2}}=\frac{7}{5}m{{r}^{2}} \\ & {{V}_{G}}={{\omega }_{O}}(R-r)={{\omega }_{K}}r \\ \end{align} \right.\)

\(\Rightarrow \omega {{'}_{O}}(R-r)={{\omega }_{K}}'r=\alpha ''(R-r)\)

Vậy: \(g\alpha +\frac{7}{5}(R-r)\alpha ''=0\Leftrightarrow \alpha ''+\frac{5g}{7(R-r)}\alpha =0.\)

Vậy quả cầu dao động điều hòa với biên độ nhỏ với chu kì: \(T=2\pi \sqrt{\frac{7(R-r)}{5g}}\)

Phương pháp động lực học.

Vì quả cẩu lăn không trượt nên K là tâm quay tức thời.

Phương trình động lực học vật rắn đối với tâm K.

 

\(-mgr\sin \alpha ={{I}_{K}}\gamma \)

 

Với \(\begin{align} & {{I}_{K}}=\frac{2}{5}m{{R}^{2}}+m{{R}^{2}}=\frac{7}{5}m{{R}^{2}}; \\ & \gamma =\frac{R-r}{r}\alpha '' \\ \end{align}\)

Kết quả thu được phương trình:

\(\alpha ''+\frac{5g}{7(R-r)}\alpha =0.\) Ta lại có kết quả trên.

Ví dụ 2. Cho cơ hệ gồm ròng rọc hình trụ khối lượng M bán kính R và lò xo có độ cứng k, vật có khối lượng m. Dây không giãn, khối lượng không đáng kể, đầu A cố định, dây không trượt trên ròng rọc. Tìm chu kì dao động của vật m.

Hướng dẫn

Phương pháp động lực học.

Xét cơ hệ tại vị trí cân bằng: F_đh  = 2P_m + P_M = Mg + 2mg = k\(\Delta {{\ell }_{o}}\)

Phương trình động lực học khi vật m ở dưới vị trí cân bằng đoạn x.

Mặt khác: V_B = V_C + ωR  = 2V_C nên x” = a_B =  2γR = 2a_C. Thay vào (1),(2),(3) ta được:

\(\left\{ \begin{array}{l} (1) \Leftrightarrow {T_B} = mg - mx''\\ (2) \Leftrightarrow {T_B} - {T_A} = \frac{M}{4}x'' \Rightarrow {T_A} = mg - mx'' - \frac{M}{4}x''\\ (3) \Leftrightarrow Mg + 2mg - k\Delta {\ell _o} - 2mx'' - \frac{M}{4}x'' - k\frac{x}{2} = \frac{M}{2}x'' \end{array} \right.\)

\(\Leftrightarrow x''+\frac{2k}{8m+3M}x=0(*)\)

Đặt: \({{\omega }^{2}}=\frac{2k}{8m+3M}\Rightarrow T=\pi \sqrt{\frac{2(8m+3M)}{k}}\)

Phương pháp năng lượng.

Chọn gốc thế năng hấp dẫn qua tâm C của ròng rọc khi ở vị trí cân bằng.

Xét hệ tại vị trí cân bằng: \(Mg+2mg=k\Delta {{\ell }_{o}}\)

Xét cơ năng của hệ.

\(W=-mgx-Mg\frac{x}{2}+\frac{1}{2}k{{(\Delta {{\ell }_{o}}+\frac{x}{2})}^{2}}+\frac{1}{2}m{{V}^{2}}+{{I}_{K}}\frac{{{\omega }^{2}}}{2}=const\)

Lấy đạo hàm hai vế với x’ = V = V_C + ωR = 2ωR; ω = α’ ta được:

\(-mgx'-Mg\frac{x'}{2}+\frac{1}{2}k2(\Delta {{\ell }_{o}}+\frac{x}{2})\frac{x'}{2}+\frac{1}{2}m2VV'+{{I}_{K}}\frac{2\omega \omega '}{2}=0\)

\(\Leftrightarrow -mgV-Mg\frac{V}{2}+k(\Delta {{\ell }_{o}}+\frac{x}{2})\frac{V}{2}+mVx''+\frac{3}{2}M\frac{V}{2}\frac{x''}{2}=0\)(*)

Với: vật m đi xuống đoạn x thì M đi xuống x/2 và quay thêm được cung có độ dài x/2 ứng với góc quay α nên: \(\frac{x}{2}=\alpha R\) hay x = 2αR hay x” = 2ω’R.

(*)  \(\Leftrightarrow k\frac{x}{4}+(m+\frac{3}{8}M)x''=0\Leftrightarrow x''+\frac{2k}{8m+3M}x=0\). Ta thu được kết quả như trên.

Ví dụ 3. Một nửa vòng xuyến mảnh bán kính R, khối lượng m thực hiện các dao động(không trượt) trên mặt nhám nằm ngang. Ở vị trí cân bằng khối tâm G của nửa vòng xuyến ở dưới tâm O đoạn d = 2R/π. Tìm chu kì dao động T1 ứng với các biên độ nhỏ?

Hướng dẫn

Khi vòng xuyến dao động với biên độ nhỏ thì tâm O của nó di chuyển trên đường nằm ngang XX’. Chọn gốc thế năng tại đường thẳng XX’.

Cơ năng của vòng xuyến tại li độ góc α.

\(W=-mgd\cos \alpha +{{I}_{K}}\frac{{{\omega }^{2}}}{2}=const(*)\)

Với: \(\left\{ \begin{align} & \omega =\alpha '\Rightarrow \omega '=\alpha '' \\ & {{I}_{O}}={{I}_{G}}+mO{{G}^{2}}\Rightarrow {{I}_{G}}-{{I}_{O}}=m{{R}^{2}}-m{{d}^{2}}=m({{R}^{2}}-{{d}^{2}}) \\ \end{align} \right.\)

\(\Rightarrow {{I}_{K}}={{I}_{G}}+m{{(R-d)}^{2}}=m2R(R-d)\)

Lấy đạo hàm hai vế của phương trình (*)

\(mgd\sin \alpha .\alpha '\text{ +  }{{\text{I}}_{K}}\frac{2\omega \alpha ''}{2}=mg\frac{2R}{\pi }\alpha \text{ + 2m}{{\text{R}}^{2}}(1-\frac{2}{\pi })\alpha ''=0\)

\(\Leftrightarrow \alpha ''+\frac{g}{R(\pi -2)}\alpha =0\)

Vậy vòng xuyến dao động điều hòa với chu kì: \(T=2\pi \sqrt{\frac{R(\pi -2)}{g}}\)

Ví dụ 4. Cho cơ hệ như hình vẽ, thanh đồng chất OC khối lượng m, chiều dài 2R có thể quay quanh trục Oz nằm ngang của một khối hình trụ cố định bán kính R. Đầu C của thanh gắn với trục của một đĩa mỏng đồng chất có bán kính R, khối lượng 2m; đĩa tiếp xúc với khối trụ. Khi cơ hệ chuyển động trong mặt phẳng xOy vuông góc với Oz, đĩa lăn không trượt trên khối trụ. Kéo thanh OC lệch góc nhỏ φo so với phương thẳng đứng rồi buông nhẹ. Tính chu kì dao động của cơ hệ. Bỏ qua ma sát ở các ổ trục và ma sát lăn giữa đĩa mỏng và khối trụ.

Hướng dẫn

Chọn gốc thế năng hấp dẫn trùng với trục Ox. Năng lượng của cơ hệ gồm thanh OC và đĩa tại li độ góc φ.

Động năng: \({{W}_{d}}={{I}_{O}}\frac{\omega _{O}^{2}}{2}+{{I}_{K}}\frac{\omega _{K}^{2}}{2}\)

Với \({{I}_{O}}=m\frac{{{(2R)}^{2}}}{12}+m{{R}^{2}}=\frac{4}{3}m{{R}^{2}}\)là momen quán tính của thanh OC đối với trục quay qua O và \({{\omega }_{O}}\)là vận tốc góc của thanh OC quay quanh O.

\({{I}_{K}}=2m\frac{{{R}^{2}}}{2}+2m{{R}^{2}}=3m{{R}^{2}}\) là momen quán tính của đĩa C quanh tâm quay tức thời K, ω_K là vận tốc góc của đĩa C quanh tâm quay tức thời K.

Mối liên hệ giữa ω_O và ω_K: V_C = ω_O.2R  = ω_K.R \(\Rightarrow \left\{ \begin{align} & {{\omega }_{K}}=2{{\omega }_{O}} \\ & {{\omega }_{O}}=~\varphi \\ & \omega {{'}_{K}}=2\omega {{'}_{O}}=2\varphi '' \\ \end{align} \right.\)(*)

Thế năng hấp dẫn: W_t = - 2m.2Rcos φ – mgRcos φ = -5mgR cos φ

Cơ năng của hệ:

\(W\text{ = }\frac{4}{3}m{{R}^{2}}.\frac{\omega _{O}^{2}}{2}+3m{{R}^{2}}\frac{{{(2{{\omega }_{O}})}^{2}}}{2}-5mgR\text{ }cos\text{ }\varphi \)

\(\Rightarrow W\text{ =}\frac{20}{3}m{{R}^{2}}\omega _{O}^{2}-5mgR\text{ }cos\text{ }\varphi =const\) (**)

Lấy đạo hàm hai vế phương trình (**):

\(\frac{20}{3}m{{R}^{2}}2{{\omega }_{O}}\omega {{'}_{O}}+5mgR\text{ sin }\varphi .\varphi '=0\) (***)

Thế (*) vào (***) ta được: \(\varphi ''+\frac{3g}{8R}\varphi =0\).

Vậy cơ hệ dao động điều hòa với chu kì: \(T=2\pi \sqrt{\frac{8R}{3g}}\)

Ví dụ 5. Một thanh AB đồng nhất, có tâm G, khối lượng m được treo trên hai dây nhẹ giống nhau AA’ và BB’ có chiều dài b. Thanh dao động trong mặt phẳng thẳng đứng, hai dây AA’ và BB’ luôn song song với nhau.

a) Tính động năng của thanh theo đạo hàm \(\alpha '\) của góc nghiêng \(\alpha \) của các dây ở một thời điểm cho trước.

b) Tìm chu kỳ dao động nhỏ của thanh.

Hướng dẫn

a) Định lý Koenig đối với động năng:

\(K=\frac{1}{2}m{{v}^{2}}(G)+{{K}^{*}}(G)\)

Trong HQC R^* (G,x,y,z) thanh đứng yên và \({{K}^{*}}(G)=0\)

Suy ra:\(K=\frac{1}{2}m{{v}^{2}}(G)=\frac{1}{2}m{{b}^{2}}\alpha {{'}^{2}}\) (1)

b) Chọn mốc thế năng tại vị trí thấp nhất của thanh trong quá trình dao động

+ Thế năng của thanh là: \(U=mgb(1-c\text{os}\alpha )\) (2)

+ Cơ năng của hệ là:

\(E=K+U=\frac{1}{2}m{{b}^{2}}\alpha {{'}^{2}}+mgb(1-c\text{os}\alpha )=mgb(1-c\text{os}{{\alpha }_{0}})=c\text{ons}t\) (3)

Đạo hàm theo thời gian hai vế của (3) ta được: \(\alpha ''b+g\sin \alpha =0\)  (4)

Với \(\alpha <{{10}^{\text{o}}}\to \sin \alpha \approx \alpha (rad)\)

thì phương trình (4) trở thành: \(\alpha ''+{{\omega }^{2}}\alpha =0\) với \({{\omega }^{2}}=\frac{g}{b}\)

Vậy chu kỳ dao động nhỏ của thanh là:  \(T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{b}{g}}\)

Ví dụ 6. Một tấm gỗ được đặt nằm ngang trên hai trục máy hình trụ có cùng bán kính, quay đều ngược chiều nhau với cùng tốc độ góc. Khoảng cách giữa hai trục của hình trụ là \(2l\). Hệ số ma sát giữa hai hình trụ và tấm gỗ đều bằng k. Tấm gỗ đang cân bằng nằm ngang, đẩy nhẹ nó khỏi vị trí cân bằng theo phương ngang một đoạn nhỏ và để tự do.

Hãy chứng minh tấm gỗ dao động điều hòa.

Hướng dẫn

Các lực tác dụng lên tấm gỗ như gồm có: Trọng lực \(m\vec{g}\); Các phản lực: \({{\vec{N}}_{1}};\,{{\vec{N}}_{2}}\) và các lực ma sát \({{\vec{F}}_{1}},{{\vec{F}}_{2}}\,\,\,\,({{F}_{1}}=k{{N}_{1}},\,{{F}_{2}}=k{{N}_{2}})\).

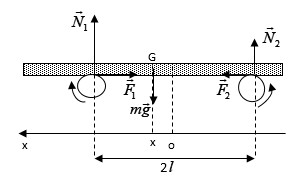
Ta luôn có: \(m\vec{g}+{{\vec{N}}_{1}}+{{\vec{N}}_{2}}=\vec{0}\)

\(\Rightarrow {{N}_{1}}+{{N}_{2}}=mg\)      (1) 

Ở VTCB \(\sum{{\vec{F}}}={{\vec{F}}_{01}}+{{\vec{F}}_{02}}=\vec{0}\) Suy ra N₀₁ = N₀₂ nên khối tâm G cách đều hai trục quay.

Chọn trục ox như hình vẽ, góc O ở VTCB, xét tấm gỗ ở vị trí có tọa độ x ,lêch khỏi VTCB một đoạn nhỏ(xem hình vẽ).

\(\sum{\vec{F}={{{\vec{F}}}_{1}}}+{{\vec{F}}_{2}}\)

Tấm gỗ không quay quanh G nên \({{M}_{{{{\vec{N}}}_{1}}}}={{M}_{{{{\vec{N}}}_{2}}}}\,hay\,{{N}_{1}}(l-x)={{N}_{2}}(l+x)\)    (2)

Suy ra N₁ > N₂, do đó F₁ >F₂ nên \(\sum{{\vec{F}}}\) có chiều của \({{\vec{F}}_{1}}\) 

Từ (1) và (2) ta có thể viết \(\frac{{{N}_{1}}}{l+x}=\frac{{{N}_{2}}}{l-x}=\frac{mg}{2l}\)                 (3)

Áp dụng định luật 2 Newton ta có: \(\sum{\vec{F}=m\vec{a}\Rightarrow {{F}_{2}}}-{{F}_{1}}=ma\Rightarrow k({{N}_{2}}-{{N}_{1}})=ma\).

Thay N₁, N₂ từ (3) và thay a=x^’’ ta có \(-k\frac{mg}{l}x=m{{x}^{''}}\Leftrightarrow {{x}^{''}}+\frac{kg}{l}x=0\) 

Điều đó chứng tỏ tấm gỗ dao động điều hòa.

 

Trên đây là một phần trích đoạn nội dung Phương pháp giải dạng bài tập về dao động của vật rắn môn Vật Lý 10 năm 2021-2022. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Các em quan tâm có thể tham khảo thêm các tài liệu cùng chuyên mục:

• Chuyên đề phương pháp giải bài tập Chuyển động thẳng đều môn Vật lý 10

• Bài tập Xác định vận tốc trung bình. Xác định các giá trị trong chuyển động thẳng đều

• Phương trình chuyển động và Đồ thị toạ độ - thời gian của Chuyển động thẳng đều

​Chúc các em học tập tốt !