Gß╗Łi ─æß║┐n c├Īc bß║Īn hß╗Źc sinh PhŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp vß╗ü ─æiß╗ćn t├Łch chuyß╗ān ─æß╗Öng m├┤n Vß║Łt L├Į 11 n─ām 2021-2022 ─æŲ░ß╗Żc chia sß║╗ dŲ░ß╗øi ─æ├óy nhß║▒m gi├║p c├Īc em c├│ th├¬m tŲ░ liß╗ću ─æß╗ā tham khß║Żo c┼®ng nhŲ░ cß╗¦ng cß╗æ kiß║┐n thß╗®c trŲ░ß╗øc khi bŲ░ß╗øc v├Āo k├¼ thi. C├╣ng tham gia giß║Żi ─æß╗ü thi ─æß╗ā ├┤n tß║Łp kiß║┐n thß╗®c v├Ā l├Ām quen vß╗øi cß║źu tr├║c ─æß╗ü thi c├Īc em nh├®, ch├║c c├Īc em thi tß╗æt!
1. T├ōM Tß║«T KIß║ŠN THß╗©C
1.1. Lß╗░C LO-REN-XŲĀ
Lß╗▒c Lo-ren-xŲĪ l├Ā lß╗▒c tß╗½ t├Īc dß╗źng l├¬n hß║Īt mang ─æiß╗ćn chuyß╗ān ─æß╗Öng trong tß╗½ trŲ░ß╗Øng. Lß╗▒c Lo-ren-xŲĪ c├│:
- ─Éiß╗ām ─æß║Ęt: Tr├¬n hß║Īt mang ─æiß╗ćn chuyß╗ān ─æß╗Öng.
- PhŲ░ŲĪng: Vu├┤ng g├│c vß╗øi mß║Ęt phß║│ng chß╗®a vectŲĪ vß║Łn tß╗æc \(\overrightarrow{v}\)cß╗¦a ─æiß╗ćn t├Łch v├Ā cß║Żm ß╗®ng tß╗½ \(\overrightarrow{B.}\)
.jpg?enablejsapi=1)
Chiều:
- Vß╗øi hß║Īt mang ─æiß╗ćn dŲ░ŲĪng: Tu├ón theo quy tß║»c
ŌĆ£B├Ān tay tr├ĪiŌĆØ: ─Éß║Ęt b├Ān tay tr├Īi sao cho c├Īc ─æŲ░ß╗Øng sß╗®c tß╗½ hŲ░ß╗øng v├Āo l├▓ng b├Ān tay, chiß╗üu tß╗½ cß╗Ģ tay ─æß║┐n c├Īc ng├│n tay l├Ā chiß╗üu chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt mang ─æiß╗ćn, chiß╗üu ng├│n c├Īi cho├Żi ra \({{90}^{o}}\)l├Ā chiß╗üu cß╗¦a lß╗▒c tß╗½.
- Vß╗øi hß║Īt mang ─æiß╗ćn ├óm: Lß╗▒c tß╗½ c├│ chiß╗üu ngŲ░ß╗Żc lß║Īi.
- ─Éß╗Ö lß╗øn: \(f=\left| q \right|vB\sin \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2.1 \right)\)
(\(\alpha \)l├Ā g├│c hß╗Żp bß╗¤i vectŲĪ vß║Łn tß╗æc \(\overrightarrow{v}\) v├Ā vectŲĪ cß║Żm ß╗®ng tß╗½ \(\overrightarrow{B}\))
1.2. CHUYß╗éN ─Éß╗śNG Cß╗”A Hß║ĀT MANG ─ÉIß╗åN TRONG ─ÉIß╗åN TRŲ»ß╗£NG V├Ć Tß╗¬ TRŲ»ß╗£NG
a. Chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt mang ─æiß╗ćn trong tß╗½ trŲ░ß╗Øng ─æß╗üu
- TrŲ░ß╗Øng hß╗Żp \(\alpha ={{90}^{o}}\left( \overrightarrow{v}\bot \overrightarrow{B} \right):\) Quß╗╣ ─æß║Īo chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt mang ─æiß╗ćn l├Ā ─æŲ░ß╗Øng tr├▓n, vß╗øi:
- B├Īn k├Łnh: \(r=\frac{mv}{\left| q \right|B}\) (2.2)
- Chu kì: \(T=\frac{2\pi r}{v}=\frac{2\pi m}{\left| q \right|B}\) (2.3)
- Tß╗æc ─æß╗Ö g├│c (tß║¦n sß╗æ xi-cl├┤-tr├┤n): \(\omega =\frac{2\pi }{T}=\frac{\left| q \right|B}{m}\) (2.4)
- TrŲ░ß╗Øng hß╗Żp \(0<\alpha <{{90}^{o}}\): Quß╗╣ ─æß║Īo chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt mang ─æiß╗ćn l├Ā ─æŲ░ß╗Øng xoß║»n ß╗æc, vß╗øi:
- B├Īn k├Łnh, chu k├¼, tß╗æc ─æß╗Ö g├│c: NhŲ░ trŲ░ß╗Øng hß╗Żp \(\alpha ={{90}^{o}}\left( \overrightarrow{v}\bot \overrightarrow{B} \right)\).
- BŲ░ß╗øc xoß║»n: \(l=\frac{2\pi v\cos \alpha .m}{\left| q \right|B}\) (2.5)
.jpg)
b. Sß╗▒ lß╗ćch cß╗¦a hß║Īt mang ─æiß╗ćn chuyß╗ān ─æß╗Öng trong ─æiß╗ćn trŲ░ß╗Øng v├Ā tß╗½ trŲ░ß╗Øng
- Sß╗▒ lß╗ćch cß╗¦a hß║Īt mang ─æiß╗ćn chuyß╗ān ─æß╗Öng trong ─æiß╗ćn trŲ░ß╗Øng: Giß║Ż sß╗Ł hß║Īt mang ─æiß╗ćn c├│ ─æiß╗ćn t├Łch q, khß╗æi lŲ░ß╗Żng m chuyß╗ān ─æß╗Öng vß╗øi vß║Łn tß╗æc \(\overrightarrow{v}\) ─æi v├Āo v├╣ng ─æiß╗ćn trŲ░ß╗Øng giß╗»a hai bß║Żn tß╗ź ─æiß╗ćn ─æß║Ęt nß║▒m ngang theo hŲ░ß╗øng vu├┤ng g├│c vß╗øi c├Īc ─æŲ░ß╗Øng sß╗®c ─æiß╗ćn (h├¼nh a).
.jpg)
Ta c├│:
- ─Éß╗Ö lß╗ćch (theo phŲ░ŲĪng thß║│ng ─æß╗®ng) cß╗¦a hß║Īt mang ─æiß╗ćn khi ─æi trong ─æiß╗ćn trŲ░ß╗Øng:
\({{y}_{1}}=\frac{\left| q \right|E}{2m}\frac{l_{1}^{2}}{v_{0}^{2}}=\frac{{{l}_{1}}}{2}\tan \alpha \) (2.6)
- ─Éß╗Ö lß╗ćch (theo phŲ░ŲĪng thß║│ng ─æß╗®ng) cß╗¦a hß║Īt mang ─æiß╗ćn khi ─æi ra khß╗Åi ─æiß╗ćn trŲ░ß╗Øng:
\({{y}_{2}}=\frac{\left| q \right|E}{m}\frac{{{l}_{1}}{{l}_{2}}}{v_{0}^{2}}={{l}_{2}}\tan \alpha \) (2.7)
- ─Éß╗Ö lß╗ćch tß╗Ģng cß╗Öng cß╗¦a hß║Īt mang ─æiß╗ćn trong qu├Ī tr├¼nh chuyß╗ān ─æß╗Öng:
\(y={{y}_{1}}+{{y}_{2}}=\frac{\left| q \right|E}{2m}\frac{l_{1}^{2}}{v_{0}^{2}}+\frac{\left| q \right|E}{m}\frac{{{l}_{1}}{{l}_{2}}}{v_{0}^{2}}=\frac{\left| q \right|E}{m}\frac{{{l}_{1}}}{v_{0}^{2}}\left( \frac{{{l}_{1}}}{2}+{{l}_{2}} \right)\)
\(=\left( \frac{{{l}_{1}}}{2}+{{l}_{2}} \right)\tan \alpha \) (2.8)
Vß╗øi: \(\tan \alpha =\frac{{{v}_{y}}}{{{v}_{0}}}=\frac{\left| q \right|E}{m}\frac{{{l}_{1}}}{v_{0}^{2}}\), \(\alpha \)l├Ā g├│c lß╗ćch chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt so vß╗øi phŲ░ŲĪng ban ─æß║¦u.
- Sß╗▒ lß╗ćch cß╗¦a hß║Īt mang ─æiß╗ćn chuyß╗ān ─æß╗Öng trong tß╗½ trŲ░ß╗Øng:
X├®t hß║Īt mang ─æiß╗ćn chuyß╗ān ─æß╗Öng ─æi v├Āo v├╣ng tß╗½ trŲ░ß╗Øng \(\overrightarrow{B}\)(h├¼nh b).
.jpg)
Ta c├│:
─Éß╗Ö lß╗ćch (theo phŲ░ŲĪng thß║│ng ─æß╗®ng) cß╗¦a hß║Īt mang ─æiß╗ćn khi
─æi trong tß╗½ trŲ░ß╗Øng:
\({{y}_{1}}=\frac{l_{1}^{2}}{2R}=\frac{\left| q \right|B}{2m}\frac{l_{1}^{2}}{{{v}_{0}}}=\frac{{{l}_{1}}}{2}\tan \beta \) (2.9)
─Éß╗Ö lß╗ćch (theo phŲ░ŲĪng thß║│ng ─æß╗®ng) cß╗¦a hß║Īt mang ─æiß╗ćn khi ─æi ra khß╗Åi tß╗½ trŲ░ß╗Øng:
\({{y}_{2}}=\frac{\left| q \right|B}{m}\frac{{{l}_{1}}{{l}_{2}}}{{{v}_{0}}}={{l}_{2}}\tan \beta \) (2.10)
─Éß╗Ö lß╗ćch tß╗Ģng cß╗Öng cß╗¦a hß║Īt mang ─æiß╗ćn trong qu├Ī tr├¼nh chuyß╗ān ─æß╗Öng:
\(y={{y}_{1}}+{{y}_{2}}=\frac{\left| q \right|B}{2m}\frac{l_{1}^{2}}{{{v}_{0}}}+\frac{\left| q \right|B}{m}\frac{{{l}_{1}}{{l}_{2}}}{{{v}_{0}}}=\frac{\left| q \right|B}{m}\frac{{{l}_{1}}}{{{v}_{0}}}\left( \frac{{{l}_{1}}}{2}+{{l}_{2}} \right)\)
\(=\left( \frac{{{l}_{1}}}{2}+{{l}_{2}} \right)\tan \beta \) (2.11)
Vß╗øi: \(\tan \beta =\frac{{{y}_{1}}}{\frac{{{l}_{1}}}{2}}=\frac{2{{y}_{1}}}{{{l}_{1}}}=\frac{\left| q \right|B{{l}_{1}}}{m{{v}_{0}}}\), \(\beta \) l├Ā g├│c lß╗ćch chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt so vß╗øi phŲ░ŲĪng ban ─æß║¦u.
1.3. HIß╗åU ß╗©NG H├öN (HALL)
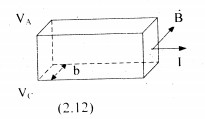
- Hiß╗ću ß╗®ng H├┤n l├Ā sß╗▒ xuß║źt hiß╗ćn hiß╗ću ─æiß╗ćn thß║┐ giß╗»a hai mß║Ęt cß╗¦a
tß║źm kim loß║Īi khi c├│ d├▓ng ─æiß╗ćn chß║Īy qua v├Ā ─æŲ░ß╗Żc ─æß║Ęt trong tß╗½
trŲ░ß╗Øng.
- Hiß╗ću ─æiß╗ćn thß║┐ H├┤n: \({{V}_{A}}-{{V}_{C}}=k\frac{IB}{b}\) (2.12)
(b l├Ā bß╗ü d├Āy cß╗¦a tß║źm kim loß║Īi; \(k=\frac{1}{{{n}_{0}}e}\): hß║▒ng sß╗æ H├┤n, \({{n}_{0}}\)l├Ā mß║Łt ─æß╗Ö electron trong kim loß║Īi)
- Ch├║ ├Į: Thß╗▒c nghiß╗ćm cho thß║źy, vß╗øi kß║┐t quß║Ż ch├Łnh x├Īc th├¼: \(k=\frac{2}{3}.\frac{1}{{{n}_{0}}e}.\)
2. PHŲ»ŲĀNG PH├üP GIß║óI
2.1. Vß╗øi dß║Īng b├Āi tß║Łp vß╗ü chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt mang ─æiß╗ćn trong ─æiß╗ćn tß╗½ trŲ░ß╗Øng.
PhŲ░ŲĪng ph├Īp giß║Żi l├Ā:
- X├Īc ─æß╗ŗnh c├Īc lß╗▒c t├Īc dß╗źng v├Āo hß║Īt mang ─æiß╗ćn. Cß╗ź thß╗ā:
- C├│ thß╗ā bß╗Å qua trß╗Źng lß╗▒c t├Īc dß╗źng v├Āo hß║Īt (nß║┐u m rß║źt nhß╗Å).
- Lß╗▒c Lo-ren-xŲĪ: ─æß╗Ö lß╗øn \(f=\left| q \right|vB\sin \alpha \), chiß╗üu ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh theo quy tß║»c ŌĆ£B├Ān tay tr├ĪiŌĆØ.
- Viß║┐t phŲ░ŲĪng tr├¼nh chuyß╗ān ─æß╗Öng cß╗¦a hß║Īt theo ─æß╗ŗnh luß║Łt II Niu-tŲĪn: \({{F}_{hl}}=ma.\)
- TrŲ░ß╗Øng hß╗Żp \(\alpha ={{90}^{o}}\), l├║c ─æ├│ quß╗╣ ─æß║Īo cß╗¦a hß║Īt l├Ā ─æŲ░ß╗Øng tr├▓n, vß╗øi:
- B├Īn k├Łnh \(R=\frac{mv}{\left| q \right|B}.\)
- Chu kì: \(T=\frac{2\pi r}{v}=\frac{2\pi m}{\left| q \right|B}.\)
- Tß╗æc ─æß╗Ö g├│c (tß║¦n sß╗æ xi-cl├┤-tr├┤n): \(\omega =\frac{2\pi }{T}=\frac{\left| q \right|B}{m}.\)
- TrŲ░ß╗Øng hß╗Żp \(0<\alpha <{{90}^{o}}\), l├║c ─æ├│ quß╗╣ ─æß║Īo cß╗¦a hß║Īt l├Ā ─æŲ░ß╗Øng xoß║»n ß╗æc, vß╗øi:
- B├Īn k├Łnh, chu k├¼, tß╗æc ─æß╗Ö g├│c nhŲ░ trŲ░ß╗Øng hß╗Żp \(\alpha ={{90}^{o}}\left( \overrightarrow{v}\bot \overrightarrow{B} \right).\)
- BŲ░ß╗øc xoß║»n: \(l=\frac{2\pi v\cos \alpha .m}{\left| q \right|B}\).
Ch├║ ├Į: C├Īc trŲ░ß╗Øng hß╗Żp phß╗®c tß║Īp cß║¦n sß╗Ł dß╗źng kiß║┐n thß╗®c ß╗¤ mß╗źc ch├║ ├Į Vß╗ü kiß║┐n thß╗®c v├Ā k─® n─āng ß╗¤ tr├¬n.
2.2. Vß╗øi dß║Īng b├Āi tß║Łp vß╗ü hiß╗ću ß╗®ng H├┤n.
PhŲ░ŲĪng ph├Īp giß║Żi l├Ā:
- Sß╗Ł dß╗źng c├Īc c├┤ng thß╗®c x├Īc ─æß╗ŗnh hiß╗ću ─æiß╗ćn thß║┐ H├┤n, hß║▒ng sß╗æ H├┤n:
\({{V}_{A}}-{{V}_{C}}=k\frac{IB}{b};k=\frac{1}{{{n}_{0}}e}\), b l├Ā bß╗ü d├Āy cß╗¦a tß║źm kim loß║Īi
- Mß╗Öt sß╗æ ch├║ ├Į: Ch├║ ├Į ─æß║┐n gi├Ī trß╗ŗ ch├Łnh x├Īc cß╗¦a hß║▒ng sß╗æ H├┤n: \(k=\frac{2}{3}\frac{1}{{{n}_{0}}e}\) nß║┐u ─æß╗ü b├Āi y├¬u cß║¦u.
3. B├ĆI Tß║¼P Vß║¼N Dß╗żNG
C├óu 1. Hß║Īt \(\alpha \) chuyß╗ān ─æß╗Öng trong tß╗½ trŲ░ß╗Øng c├│ cß║Żm ß╗®ng tß╗½ \(B=1,2T\) theo quß╗╣ ─æß║Īo tr├▓n c├│ b├Īn k├Łnh 0,45m. T├Łnh vß║Łn tß╗æc v, chu k├¼ quay T, ─æß╗Öng n─āng W cß╗¦a hß║Īt trong tß╗½ trŲ░ß╗Øng v├Ā hiß╗ću ─æiß╗ćn thß║┐ U cß║¦n thiß║┐t ─æ├Ż d├╣ng ─æß╗ā t─āng tß╗æc cho hß║Īt trŲ░ß╗øc khi ─æi v├Āo tß╗½ trŲ░ß╗Øng. Biß║┐t hß║Īt \(\alpha \) l├Ā hß║Īt nh├ón nguy├¬n tß╗Ł heli c├│ khß╗æi lŲ░ß╗Żng bß║▒ng 4 lß║¦n khß╗æi lŲ░ß╗Żng pr├┤t├┤n, c├│ ─æiß╗ćn t├Łch +2e, khß╗æi lŲ░ß╗Żng pr├┤t├┤n gß║źp 1840 lß║¦n khß╗æi lŲ░ß╗Żng ├¬lectr├┤n.
B├Āi giß║Żi
- Lß╗▒c tß╗½ t├Īc dß╗źng l├¬n hß║Īt \(\alpha \): \(F=\left| q \right|vB.\sin \alpha =\left| q \right|vB\) (v├¼ \(\alpha ={{90}^{o}}\))
- V├¼ hß║Īt chuyß╗ān ─æß╗Öng theo quß╗╣ ─æß║Īo tr├▓n n├¬n lß╗▒c F ─æ├│ng vai tr├▓ l├Ā lß╗▒c hŲ░ß╗øng t├óm:
\(F=ma=m\frac{{{v}^{2}}}{R}\Leftrightarrow \left| q \right|vB=m\frac{{{v}^{2}}}{R}\Rightarrow v=\frac{\left| q \right|BR}{m}\)
Trong đó: \(q=+2e=2.1,{{6.10}^{-19}}=3,{{2.10}^{-19}}C;\,\,m=4{{m}_{p}}=4,1840{{m}_{e}}\)
\(\Rightarrow m=4,1840.9,{{1.10}^{-31}}=6,{{6976.10}^{-27}}\text{kg}\text{.}\)
\(\Rightarrow v=\frac{3,{{2.10}^{-19}}.1,2.0,45}{6,{{6976.10}^{-27}}}\approx 2,{{6.10}^{7}}.\)
- Chu kì: \(T=\frac{2\pi R}{v}=\frac{2.3,14.0,45}{2,{{6.10}^{7}}}\approx 1,{{1.10}^{-7}}\text{s}\text{.}\)
- ─Éß╗Öng n─āng:
\(W=\frac{1}{2}m{{v}^{2}}=\frac{1}{2}.6,{{6976.10}^{-27}}.{{\left( 2,{{6.10}^{7}} \right)}^{2}}=2,{{26.10}^{-12}}\text{J}={{14.10}^{6}}\text{eV}=14\,\text{MeV}\text{.}\)
(LŲ░u ├Į: \(1\text{eV}=1,{{6.10}^{-19}}\text{J}\))
- ├üp dß╗źng ─æß╗ŗnh l├Ł ─æß╗Öng n─āng ta c├│: \(\Delta {{W}_{\tilde{n}}}=A.\)
\(\Rightarrow W-0=qU\Rightarrow U=\frac{W}{q}=\frac{{{14.10}^{6}}\text{eV}}{2.\text{e}}={{7.10}^{6}}\text{V}\text{.}\)
C├óu 2: ├Ŗlectr├┤n chuyß╗ān ─æß╗Öng trong mß╗Öt tß╗½ trŲ░ß╗Øng ─æß╗üu c├│ cß║Żm ß╗®ng tß╗½ B. Tß║Īi thß╗Øi ─æiß╗ām ban ─æß║¦u ├¬lectr├┤n ß╗¤ ─æiß╗ām O v├Ā vß║Łn tß╗æc cß╗¦a n├│ vu├┤ng g├│c \(\overrightarrow{B}\). T├¼m khoß║Żng c├Īch tß╗½ O ─æß║┐n ├¬lectr├┤n tß║Īi thß╗Øi ─æiß╗ām t. Khß╗æi lŲ░ß╗Żng m, ─æiß╗ćn t├Łch e v├Ā vß║Łn tß╗æc v cß╗¦a ├¬lectr├┤n coi nhŲ░ ─æ├Ż biß║┐t.
B├Āi giß║Żi
V├¼ vß║Łn tß╗æc \(\overrightarrow{v}\) vu├┤ng g├│c vß╗øi \(\overrightarrow{B}\) n├¬n hß║Īt chuyß╗ān ─æß╗Öng theo quß╗╣ ─æß║Īo tr├▓n vß╗øi b├Īn k├Łnh: \(R=\frac{mv}{eB}\) v├Ā tß║¦n sß╗æ g├│c: \(\omega =\frac{v}{R}=\frac{eB}{m}.\)
.jpg)
Tß╗½ ─æ├│, g├│c m├Ā b├Īn k├Łnh nß╗æi tß╗½ t├óm ─æß║┐n hß║Īt quay ─æŲ░ß╗Żc trong thß╗Øi gian t l├Ā:
\(\varphi =\omega t=\frac{eB}{m}t\)
Ta c├│: \(OH=2OI=2R.\sin \frac{\varphi }{2}=\frac{2mv}{eB}.\sin \left( \frac{eB}{2m}.t \right)\)
Vß║Ły: Khoß║Żng c├Īch tß╗½ O ─æß║┐n ├¬lectr├┤n tß║Īi thß╗Øi ─æiß╗ām t l├Ā: \(l=\frac{2mv}{eB}.\sin \left( \frac{eB}{2m}.t \right).\)
C├óu 3. M├Īy ph├Īt ─æiß╗ćn tß╗½ thuß╗Ę ─æß╗Öng (MHD). Tß╗ź phß║│ng diß╗ćn t├Łch mß╗Śi bß║Żn l├Ā S, khoß║Żng c├Īch giß╗»a hai bß║Żn l├Ā d ─æŲ░ß╗Żc ─æß║Ęt trong mß╗Öt d├▓ng plasma dß║½n ─æiß╗ćn c├│ ─æiß╗ćn trß╗¤ suß║źt \(\rho \). Plasma chß║Ży vß╗øi vß║Łn tß╗æc \(\overrightarrow{v}\) kh├┤ng ─æß╗Ģi song song hai bß║Żn. Hß╗ć thß╗æng ─æŲ░ß╗Żc ─æß║Ęt trong tß╗½ trŲ░ß╗Øng c├│ \(\overrightarrow{B}\) song song hai bß║Żn v├Ā vu├┤ng g├│c \(\overrightarrow{v}\). Hai bß║Żn tß╗ź ─æiß╗ćn nß╗æi vß╗øi mß╗Öt ─æiß╗ćn trß╗¤ R.
a. Giß║Żi th├Łch tß║Īi sao tß╗ź ─æiß╗ćn lß║Īi c├│ t├Īc dß╗źng nhŲ░ mß╗Öt nguß╗ōn ─æiß╗ćn cung cß║źp d├▓ng ─æiß╗ćn kh├┤ng ─æß╗Ģi cho R? T├Łnh c├┤ng suß║źt ti├¬u thß╗ź cß╗¦a R.
b. Vß╗øi gi├Ī trß╗ŗ n├Āo cß╗¦a R, c├┤ng suß║źt l├Ā cß╗▒c ─æß║Īi? T├Łnh gi├Ī trß╗ŗ cß╗▒c ─æß║Īi n├Āy.
├üp dß╗źng sß╗æ:
\(\text{S}=1{{\text{m}}^{\text{2}}};\,\,\text{d}=1\text{m;}\,\,\text{B}=\text{2T;}\,\,\rho ={{10}^{2}}\Omega \text{m;}\,\,\text{v}=\text{1000m/s}\text{.}\)
B├Āi giß║Żi
a. C├┤ng suß║źt ti├¬u thß╗ź cß╗¦a R
- Giß║Żi th├Łch:
.jpg)
V├¼ d├▓ng plasma dß║½n ─æiß╗ćn n├¬n khi chuyß╗ān ─æß╗Öng trong tß╗½ trŲ░ß╗Øng \(\overrightarrow{B}\) th├¼ sß║Į chß╗ŗu t├Īc dß╗źng cß╗¦a lß╗▒c tß╗½.
V├¼ vß║Łn tß╗æc \(\overrightarrow{v}\) cß╗¦a d├▓ng plasma vu├┤ng g├│c vß╗øi \(\overrightarrow{B}\) n├¬n lß╗▒c tß╗½ t├Īc dß╗źng l├¬n d├▓ng plasma vu├┤ng g├│c vß╗øi c├Īc bß║Żn tß╗ź. DŲ░ß╗øi t├Īc dß╗źng cß╗¦a lß╗▒c tß╗½ n├Āy dß║½n ─æß║┐n sß╗▒ ph├ón bß╗Ģ ─æiß╗ćn t├Łch tr├Īi dß║źu tr├¬n hai bß║Żn cß╗¦a tß╗ź.
Khi nß╗æi hai bß║Żn tß╗ź vß╗øi ─æiß╗ćn trß╗¤ R th├¼ sß║Į c├│ d├▓ng ─æiß╗ćn qua R, khi ─æ├│ tß╗ź ─æiß╗ćn ─æ├│ng vai tr├▓ nhŲ░ mß╗Öt nguß╗ōn ─æiß╗ćn.
- T├Łnh c├┤ng suß║źt ti├¬u thß╗ź tr├¬n R:
Ta c├│: \(P={{I}^{2}}R\) (1)
Vß╗øi \(I=\frac{E}{R+{{R}_{t}}}\) (2)
(\({{R}_{t}}\): l├Ā ─æiß╗ćn trß╗¤ cß╗¦a phß║¦n plasma nß║▒m trong kh├┤ng gian giß╗»a hai bß║Żn cß╗¦a tß╗ź; E: l├Ā suß║źt ─æiß╗ćn ─æß╗Öng).
Ta c├│: \({{R}_{t}}=\rho .\frac{d}{S}\,\,\,\left( 3 \right)\) v├Ā \(E=\frac{A}{q}\)
(vß╗øi q l├Ā ─æiß╗ćn t├Łch cß╗¦a d├▓ng plasma; A l├Ā c├┤ng cß╗¦a lß╗▒c ─æiß╗ćn l├Ām di chuyß╗ān q tß╗½ bß║Żn n├Āy sang bß║Żn kia cß╗¦a tß╗ź).
\(\Rightarrow A=Fd=qvBd;\,\,\,\,E=vBd\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\)
- Thay (4) v├Āo (2), ta ─æŲ░ß╗Żc: \(I=\frac{vBd}{\left( R+\rho \frac{d}{S} \right)}\,\,\,\,\,\,\,\,\,\,\,\left( 5 \right)\)
- Thay (5) v├Āo (1), ta ─æŲ░ß╗Żc: \(P=\frac{{{v}^{2}}{{B}^{2}}{{d}^{2}}}{{{\left( R+\rho \frac{d}{S} \right)}^{2}}}.R.\)
Vß║Ły: C├┤ng suß║źt ti├¬u thß╗ź cß╗¦a R l├Ā \(P=\frac{{{v}^{2}}{{B}^{2}}{{d}^{2}}}{{{\left( R+\rho \frac{d}{S} \right)}^{2}}}.R\)
b. X├Īc ─æß╗ŗnh R ─æß╗ā c├┤ng suß║źt P ─æß║Īt cß╗▒c ─æß║Īi
Ta c├│: \(p=\frac{{{v}^{2}}{{B}^{2}}{{d}^{2}}}{{{\left( R+\rho \frac{d}{S} \right)}^{2}}}.R\Rightarrow P={{P}_{\max }}\) khi \({{\left( R+\rho \frac{d}{S} \right)}_{\min }}\).
- Theo bß║źt ─æß║│ng thß╗®c C├┤-si, ta c├│: \(R+\rho \frac{d}{S}\ge 2\sqrt{R.\rho \frac{d}{S}}.\)
\(\Rightarrow {{\left( R+\rho \frac{d}{S} \right)}_{\min }}=2\sqrt{R.\rho \frac{d}{S}}\) khi v├Ā chß╗ē khi \(R=\rho \frac{d}{S}.\)
V├Ā \(P={{P}_{\max }}=\frac{{{v}^{2}}{{B}^{2}}{{d}^{2}}}{4\rho \frac{d}{S}}=\frac{{{v}^{2}}{{B}^{2}}dS}{4\rho }.\)
- ├üp dß╗źng sß╗æ: \(R={{10}^{-2}}.\frac{1}{1}={{10}^{-2}}\Omega .\)
V├Ā \({{P}_{\max }}=\frac{{{1000}^{2}}{{.2}^{2}}.1.1}{{{4.10}^{-2}}}={{10.10}^{7}}W={{10}^{5}}kW.\)
Vß║Ły: ─Éß╗ā \(P={{P}_{\max }}\) th├¼ \(R={{10}^{-2}}\Omega \) v├Ā \({{P}_{\max }}={{10}^{5}}kW.\)
C├óu 4. Hai hß║Īt nhß╗Å giß╗æng nhau, c├│ ─æiß╗ćn t├Łch q v├Ā khß╗æi lŲ░ß╗Żng m, chuyß╗ān ─æß╗Öng ─æß╗ōng thß╗Øi tß╗½ mß╗Öt ─æiß╗ām theo phŲ░ŲĪng vu├┤ng g├│c vß╗øi vectŲĪ cß║Żm ß╗®ng tß╗½ \(\overrightarrow{B}\) trong mß╗Öt tß╗½ trŲ░ß╗Øng ─æß╗üu. H├Ży biß╗āu diß╗ģn khoß║Żng c├Īch giß╗»a hai hß║Īt theo thß╗Øi gian, nß║┐u vß║Łn tß╗æc ─æß║¦u cß╗¦a ch├║ng c├╣ng chiß╗üu v├Ā bß║▒ng \(\overrightarrow{{{v}_{1}}}\) v├Ā \(\overrightarrow{{{v}_{2}}}\). Bß╗Å qua tŲ░ŲĪng t├Īc t─®nh ─æiß╗ćn giß╗»a hai hß║Īt ─æiß╗ćn.
B├Āi giß║Żi
- Giß║Ż sß╗Ł ban ─æß║¦u hai hß║Īt c├╣ng ß╗¤ ─æiß╗ām O. Sau thß╗Øi gian chuyß╗ān ─æß╗Öng hß║Īt thß╗® nhß║źt ─æß║┐n A, hß║Īt thß╗® hai ─æß║┐n B.
.jpg)
- Ta c├│: \(OA=\frac{2m{{v}_{1}}}{qB}\sin \left( \frac{qB}{2m}t \right);\)
\(OB=\frac{2m{{v}_{2}}}{qB}\sin \left( \frac{qB}{2m}t \right).\)
- V├¼ vß║Łn tß╗æc g├│c cß╗¦a hß║Īt thß╗® nhß║źt v├Ā hß║Īt thß╗® hai ─æß╗üu bß║▒ng nhau v├Ā bß║▒ng \(\omega =\frac{qB}{m}\) n├¬n trong c├╣ng thß╗Øi gian t th├¼ g├│c quay \(\varphi \) cß╗¦a hai b├Īn k├Łnh ─æß╗üu bß║▒ng nhau (h├¼nh vß║Į), suy ra ba ─æiß╗ām O, A, B nß║▒m tr├¬n c├╣ng ─æŲ░ß╗Øng thß║│ng.
\(\Rightarrow AB=OB-OA=\frac{2m}{qB}\left( {{v}_{2}}-{{v}_{1}} \right)\sin \left( \frac{qB}{2m}.t \right)\)
Vß║Ły: Khoß║Żng c├Īch giß╗»a hai hß║Īt l├Ā: \(r\left( t \right)=\frac{2m}{qB}\left( {{v}_{2}}-{{v}_{1}} \right)\sin \left( \frac{qB}{2m}.t \right)\), vß╗øi \({{v}_{2}}>{{v}_{1}}.\)
---(─Éß╗ā xem ─æß║¦y ─æß╗¦, chi tiß║┐t cß╗¦a t├Āi liß╗ću vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)---
Tr├¬n ─æ├óy l├Ā tr├Łch dß║½n mß╗Öt phß║¦n nß╗Öi dung t├Āi liß╗ću PhŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp vß╗ü ─æiß╗ćn t├Łch chuyß╗ān ─æß╗Öng m├┤n Vß║Łt L├Į 11 n─ām 2021-2022. ─Éß╗ā xem th├¬m nhiß╗üu tŲ░ liß╗ću hß╗»u ├Łch kh├Īc, c├Īc em ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm













