Giải Toán 12 SGK nâng cao Ôn tập Chương 2 Mặt cầu, mặt trụ, mặt nón

Cho mp  (P) và điểm A không thuộc (P). Chứng minh rằng mọi mặt cầu đi qua A và có tâm nằm trên (P) luôn luôn đi qua hai điểm cố định.

Hướng dẫn giải:

 

Lấy điểm O nằm trên mp (P). Gọi (S) là mặt cầu đi qua A có tâm O.

Gọi A′ là điểm đối xứng của A qua mp (P) ta có OA′ = OA = R nên (S) đi qua A′. Vậy mặt cầu (S) luôn đi qua hai điểm cố định A và A′.

---

Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp S.ABC, biết \(SA = SB = SC = a,\widehat {ASB} = {60^0},\widehat {BSC} = {90^0},\widehat {CSA} = {120^0}\)

Hướng dẫn giải:

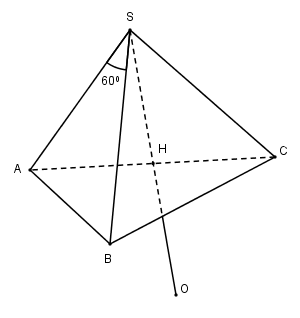
Áp dụng định lí Cosin trong tam giác SAB, SAC ta có:

\(\begin{array}{l}
A{B^2} = S{A^2} + S{B^2} - 2SA.SB.cos{60^0}\\
 = {a^2} + {a^2} - 2{a^2}.\frac{1}{2} = {a^2} \Rightarrow AB = a\\
A{C^2} = S{A^2} + S{C^2} - 2SA.SC.cos{120^0}\\
 = {a^2} + {a^2} - 2{a^2}\left( { - \frac{1}{2}} \right) = 3{a^2} \Rightarrow AC = a\sqrt 3 
\end{array}\)

Trong tam giác vuông SBC có \(B{C^2} = S{B^2} + S{C^2} = 2{a^2} \Rightarrow BC = a\sqrt 2 \)

Ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow \Delta ABC\) vuông tại B

Gọi H là trung điểm của AC thì H là tâm đường tròn ngoại tiếp tam giác ABC.

Vì SA = SB = SC nên SH ⊥ mp(ABC)

Và \(S{H^2} = S{C^2} - H{C^2} = {a^2} - {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{{a^2}}}{4} \Rightarrow SH = \frac{a}{2}\)

Gọi O là điểm đối xứng của S qua H thì SO = OA = OB = OC = a nên mặt cầu ngoại tiếp hình chóp S.ABC có tâm O và bán kính R = a.

---

Cho hai đường tròn (O;r) và (O′;r′) cắt nhau tại hai điểm A, B và lần lượt nằm trên hai mặt phẳng phân biệt (P) và (P′).

a) Chứng minh rằng có mặt cầu (S) đi qua hai đường tròn đó.

b) Tìm bán kính R của mặt cầu (S) khi \(r = 5,r' = \sqrt {10} ,AB = 6,OO\prime  = \sqrt {21} \)

Hướng dẫn giải:

Câu a:

Gọi M là trung điểm của AB ta có: OM ⊥ AB và O′M ⊥ AB => AB ⊥ (OO′M)

Gọi Δ, Δ′ lần lượt là trục của đường tròn (O;r) và (O′;r′) thì AB ⊥ Δ, AB ⊥ Δ′. Do đó Δ, Δ′ cùng nằm trong mp (OO′M)

Gọi I là giao điểm của Δ và Δ′ thì I là tâm của mặt cầu (S) đi qua hai đường tròn (O;r) và (O′;r′) và S có bán kính R = IA.

Câu b:

Ta có: \(MA = MB = 3,OA = r = 5,OA\prime  = r\prime  = \sqrt {10} \)

\(\begin{array}{l}
OM = \sqrt {O{A^2} - A{M^2}}  = \sqrt {25 - 9}  = 4\\
O\prime M = \sqrt {O\prime {A^2} - A{M^2}}  = \sqrt {10 - 9}  = 1
\end{array}\)

Áp dụng định lí Cosin trong ΔOMO′ ta có:

\(\begin{array}{l}
OO{\prime ^2} = O{M^2} + O\prime {M^2} - 2OM.O\prime M.cos\widehat {OMO\prime }\\
 \Rightarrow 21 = 16 + 1 - 2.4.1.cos\widehat {OMO\prime } \Rightarrow cos\widehat {OMO\prime } =  - \frac{1}{2}\\
\widehat {OMO\prime } = {120^0},\widehat {OIO\prime } = {60^0}
\end{array}\)

Áp dụng định lí Côsin trong tam giác OMO′ ta có:

\(\begin{array}{l}
M{O^2} = MO{\prime ^2} + OO{\prime ^2} - 2MO\prime .OO\prime .cos\widehat {MO\prime O}\\
 \Rightarrow cos\widehat {MO\prime O} = \frac{{\sqrt {21} }}{7} \Rightarrow sin\widehat {OO\prime I} = \frac{{\sqrt {21} }}{7}
\end{array}\)

Áp dụng định lí Cosin trong tam giác OIO′ ta có: 

\(\begin{array}{l}
\frac{{OI}}{{sin\widehat {OO\prime I}}} = \frac{{OO\prime }}{{sin\widehat {OIO\prime }}} \Leftrightarrow \frac{{OI}}{{\frac{{\sqrt {21} }}{7}}} = \frac{{\sqrt {21} }}{{\frac{{\sqrt 3 }}{2}}} \Leftrightarrow OI = 2\sqrt 3 \\
 \Rightarrow R = \sqrt {O{A^2} + O{I^2}}  = \sqrt {25 + 12}  = \sqrt {37} 
\end{array}\)

---

Cho hình nón (N) sinh bởi tam giác đều cạnh aa khi quay quanh một đường cao của tam giác đó.

a) Một mặt cầu có diện tích bằng diện tích toàn phần của hình nón (N) thì có bán kính bằng bao nhiêu?

b) Một khối cầu có thể tích của khối nón (N) thì có bán kính bằng bao nhiêu?

Hướng dẫn giải:

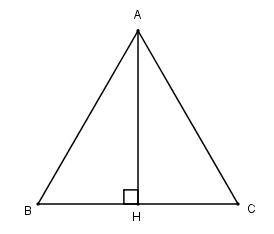
Hình nón (N) có bán kính đáy \(r = BH = \frac{1}{2}a\), chiều cao \(h = AH = \frac{{a\sqrt 3 }}{2}\) và đường sinh l = AB = a.

Diện tích toàn phần \({S_{tp}} = {S_{xq}} + {S_d} = \pi rl + \pi {r^2} = \pi \frac{{{a^2}}}{2} + \pi \frac{{{a^2}}}{4} = \frac{3}{4}\pi {a^2}\)

Thể tích \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi \frac{{{a^2}}}{4}.\frac{{a\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{{24}}\pi {a^3}\)

Câu a:

Nếu mặt cầu có bán kính R thì diện tích bằng 4πR² nên 

\(4\pi {R^2} = \frac{3}{4}\pi {a^2} \Rightarrow R = \frac{{a\sqrt 3 }}{4}\)

Câu b:

Nếu khối cầu có bán kính R thì thể tích bằng \(\frac{4}{3}\pi {R^3}\) nên

\(\frac{4}{3}\pi {R^3} = \frac{{\sqrt 3 }}{{24}}\pi {a^3} \Rightarrow R = \frac{{\sqrt[6]{{12}}}}{4}a\)

---

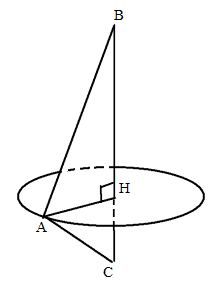
Cho tam giác ABC vuông tại A, AB = c, AC = b . Gọi V₁, V₂, V₃  là thể tích các khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi lần lượt quay quanh AB, AC, BC.

a) Tính V₁, V₂, V₃ theo b, c

b) Chứng minh rằng \(\frac{1}{{V_3^2}} = \frac{1}{{V_1^2}} + \frac{1}{{V_2^2}}\)

Hướng dẫn giải:

Câu a:

Khi quay tam giác ABC quanh AB ta được khối nón có chiều cao AB = c và bán kính đáy AC = b nên có thể tích \({V_1} = \frac{1}{3}\pi c{b^2}\)

Tương tự khi quay tam giác ABC quanh AC ta được khối nón có thể tích \({V_2} = \frac{1}{3}\pi b{c^2}\)

Gọi AH là chiều cao của tam giác ABC. Khi quay tam giác ABC quanh BC ta được hai khối nón sinh bởi hai tam giác ABH và ACH.

Khi đó ta có 

\(\begin{array}{l}
{V_3} = \frac{1}{3}\pi A{H^2}.BH + \frac{1}{3}\pi A{H^2}.CH = \frac{1}{3}\pi AH.BC\\
 = \frac{1}{3}\pi {(bc\sqrt {{b^2} + {c^2}} )^2}\sqrt {{b^2} + {c^2}}  = \frac{1}{3}\frac{{\pi {b^2}{c^2}}}{{\sqrt {{b^2} + {c^2}} }}
\end{array}\)

Câu b:

Ta có:

\(\begin{array}{l}
\frac{1}{{V_3^2}} = \frac{{9({b^2} + {c^2})}}{{\pi {b^4}{c^4}}}\\
\frac{1}{{V_1^2}} + \frac{1}{{V_2^2}} = \frac{9}{{\pi {c^2}{b^4}}} + \frac{9}{{\pi {b^2}{c^4}}} = \frac{{9({b^2} + {c^2})}}{{\pi {b^4}{c^4}}} = \frac{1}{{V_3^2}}
\end{array}\)

---

Một hình thang cân ABCD có các cạnh đáy AB = 2a, BD = 4a, cạnh bên AD = BC = 3a. Hãy tính thể tích và diện tích toàn phần của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó.

Hướng dẫn giải:

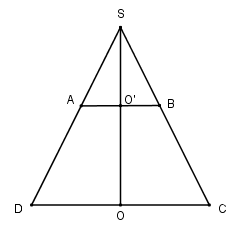
Gọi S là giao điểm của hai cạnh bên AD và BC của hình thang. Đường cao SO của tam giác cân SCD là trục đối xứng của hình thang, do đó SO cắt AB tại trung điểm O′ của AB.

Khi quay quanh SO, tam giác SCD sinh ra khối nón (N₁) có thể tích V₁, tam giác SAB sinh ra khối nón (N₂) có thể tích V₂, còn hình thang ABCD sinh ra một khối tròn xoay (H) có thể tích V = V₁ − V₂.

Vì \(AB = \frac{1}{2}CD\) nên AB là đường trung bình của tam giác SCD nên SB = BC = 3a.

Ta có: 

\(\begin{array}{l}
SO\prime  = \sqrt {S{B^2} - O\prime {B^2}}  = \sqrt {9{a^2} - {a^2}}  = 2\sqrt 2 a\\
SO = 2SO\prime  = 4\sqrt 2 a\\
V = {V_1} - {V_2} = \frac{1}{3}\pi O{C^2}.SO - \frac{1}{3}\pi O\prime {B^2}.SO\prime  = \frac{1}{3}\pi 4{a^2}.SO - \frac{1}{3}\pi {a^2}SO\prime \\
 = \frac{1}{4}\pi {a^2}(4SO - SO\prime ) = \frac{1}{3}\pi {a^2}(16\sqrt 2 a - 2\sqrt 2 a) = \frac{{14\sqrt 2 }}{3}\pi {a^3}
\end{array}\)

Diện tích xung quanh của khối tròn xoay (H) là

\(\begin{array}{l}
{S_{xq}} = {S_1} - {S_2} = \pi OC.SC - \pi O\prime B.SB = 9\pi {a^2}\\
{S_{tp}} = {S_{xq}} + {S_d} = 9\pi {a^2} + \pi {a^2} + 4\pi {a^2} = 14\pi {a^2}
\end{array}\)

 

Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Toán 12 Ôn tập Chương 2 Mặt cầu, mặt trụ, mặt nón được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 12 học tập thật tốt!