DŲ░ß╗øi ─æ├óy l├Ā HŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp To├Īn 11 n├óng cao ChŲ░ŲĪng 5 Luyß╗ćn tß║Łp trang 212 - 213 ─æŲ░ß╗Żc hoc247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp, nß╗Öi dung b├Īm s├Īt theo chŲ░ŲĪng tr├¼nh SGK To├Īn 11 n├óng cao gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n tß║Łp kiß║┐n thß╗®c hiß╗ću quß║Ż hŲĪn.
B├Āi 33 trang 212 SGK To├Īn 11 n├óng cao
T├¼m ─æß║Īo h├Ām cß╗¦a mß╗Śi h├Ām sß╗æ sau :
\(\begin{array}{l}
a)y = \frac{{sinx}}{x} + \frac{x}{{sinx}}\\
b)y = \frac{{si{n^2}x}}{{1 + tan2x}}\\
c)y = tan(sinx)\\
d)y = xcot({x^2} - 1)\\
e)y = co{s^2}\sqrt {\frac{\pi }{4} - 2x} \\
f)y = x\sqrt {sin3x}
\end{array}\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
\(\begin{array}{l}
y' = \frac{{{{\left( {\sin x} \right)}^\prime }.x - \sin x.\left( {x'} \right)}}{{{x^2}}} + \frac{{x\prime sinx - x.(sinx)\prime }}{{si{n^2}x}}\\
= \frac{{xcosx - sinx}}{{{x^2}}} + \frac{{sinx - xcosx}}{{si{n^2}x}}\\
= (xcosx - sinx)\left( {\frac{1}{{{x^2}}} - \frac{1}{{si{n^2}x}}} \right)
\end{array}\)
Câu b:
\(\begin{array}{l}
y' = \frac{{{{\left( {{{\sin }^2}x} \right)}^\prime }.\left( {1 + \tan 2x} \right) - {{\sin }^2}x\left( {1 + \tan 2x} \right)'}}{{{{\left( {1 + \tan 2x} \right)}^2}}}\\
= \frac{{2\sin x\left( {sinx} \right)'\left( {1 + \tan 2x} \right) - {{\sin }^2}x\left( {2x} \right)'.\left( {1 + {{\tan }^2}2x} \right)}}{{{{\left( {1 + {{\tan }^2}2x} \right)}^2}}}\\
= \frac{{2\sin x\cos x\left( {1 + \tan 2x} \right) - {{\sin }^2}x.2\left( {1 + {{\tan }^2}2x} \right)}}{{{{\left( {1 + \tan 2x} \right)}^2}}}\\
= \frac{{\sin 2x}}{{1 + \tan 2x}} - \frac{{2{{\sin }^2}x\left( {1 + {{\tan }^2}2x} \right)}}{{{{\left( {1 + \tan 2x} \right)}^2}}}
\end{array}\)
Câu c:
\(y' = {\left( {\sin x} \right)^\prime }.\frac{1}{{{{\cos }^2}\left( {\sin x} \right)}} = \frac{{cosx}}{{co{s^2}(sinx)}}\)
Câu d:
\(\begin{array}{l}
y' = x'.\cot \left( {{x^2} - 1} \right) + x.{\left[ {\cot \left( {{x^2} - 1} \right)} \right]^\prime }\\
= cot({x^2} - 1) + x.({x^2} - 1)\prime .\frac{{ - 1}}{{sin2({x^2} - 1)}}\\
= cot({x^2} - 1) + x.\frac{{ - 2x}}{{si{n^2}({x^2} - 1)}}\\
= cot({x^2} - 1) - \frac{{2{x^2}}}{{si{n^2}({x^2} - 1)}}
\end{array}\)
Câu e:
\(\begin{array}{l}
y' = 2{\left( {co{\mathop{\rm s}\nolimits} \sqrt {\frac{\pi }{4} - 2x} } \right)^\prime }.co{\mathop{\rm s}\nolimits} \sqrt {\frac{\pi }{4} - 2x} \\
= 2{\left( {\sqrt {\frac{\pi }{4} - 2x} } \right)^'}.\left( { - \sin \sqrt {\frac{\pi }{4} - 2x} } \right).co{\mathop{\rm s}\nolimits} \sqrt {\frac{\pi }{4} - 2x} \\
= \frac{{{{\left( {\frac{\pi }{4} - 2x} \right)}^'}}}{{2.\sqrt {\frac{\pi }{4} - 2x} }}.\left( { - 2\sin \sqrt {\frac{\pi }{4} - 2x} .\cos \sqrt {\frac{\pi }{4} - 2x} } \right)\\
= \frac{{ - 2}}{{2\sqrt {\frac{\pi }{4} - 2x} }}.\left( { - \sin 2\sqrt {\frac{\pi }{4} - 2x} } \right) = \frac{{2\sin \sqrt {\pi - 8x} }}{{\sqrt {\pi - 8x} }}
\end{array}\)
Câu f:
\(\begin{array}{l}
y' = x'\sqrt {\sin 3x} + x.{\left( {\sqrt {\sin 3x} } \right)^\prime } = \sqrt {sin3x} + x.\frac{{(sin3x)\prime }}{{2\sqrt {sin3x} }}\\
= \sqrt {sin3x} + x.\frac{{3cos3x}}{{2\sqrt {sin3x} }} = \frac{{2sin3x + 3xcos3x}}{{2\sqrt {sin3x} }}
\end{array}\)
B├Āi 34 trang 212 SGK To├Īn 11 n├óng cao
T├Łnh fŌĆ▓(ŽĆ) nß║┐u \(f(x) = \frac{{sinx - xcosx}}{{cosx - xsinx}}\)
HŲ░ß╗øng dß║½n giß║Żi:
Vß╗øi mß╗Źi x sao cho cosx ŌłÆ xsinx ŌēĀ 0, ta c├│:
\(f\prime (x) = \frac{{[cosx - (cosx - xsinx)](cosx - xsinx) - (sinx - xcosx)[ - sinx - (sinx + xcosx)]}}{{{{(cosx - xsinx)}^2}}}\)
V├¼ sinŽĆ = 0, cosŽĆ = ŌłÆ1 n├¬n: \(f\prime (\pi ) = \frac{{[ - 1 - ( - 1)].( - 1) - \pi .\pi }}{{{{( - 1)}^2}}} = - {\pi ^2}\)
B├Āi 35 trang 212 SGK To├Īn 11 n├óng cao
Giß║Żi phŲ░ŲĪng tr├¼nh yŌĆÖ = 0 trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau :
a. y = sin2x - 2cosx
b. y = 3sin2x + 4cos2x + 10x
c. y=cos2x + sinx
d. y = tanx + cotx
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Vß╗øi mß╗Źi R, ta c├│:
\(\begin{array}{l}
y' = 2\cos 2x + 2\sin x = 2\left( {1 - 2{{\sin }^2}x} \right) + 2\sin x\\
= - 4si{n^2}x + 2sinx + 2
\end{array}\)
Vß║Ły \(y\prime = 0 \Leftrightarrow 2si{n^2}x - sinx - 1 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}
sinx = 1\\
sinx = - \frac{1}{2}
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{2} + k2\pi \\
x = - \frac{\pi }{6} + k2\pi \\
x = \frac{{7\pi }}{6} + k2\pi (k \in Z)
\end{array} \right.\)
Câu b:
Vß╗øi mß╗Źi x Ōłł R, ta c├│: yŌĆ▓ = 6cos2x ŌłÆ 8sin2x + 10
Vß║Ły yŌĆ▓ = 0 <=> 4sin2xŌłÆ3cos2x = 5
\( \Leftrightarrow \frac{4}{5}sin2x - \frac{3}{5}cos2x = 1(1)\)
V├¼ \({\left( {\frac{4}{5}} \right)^2} + {\left( {\frac{3}{5}} \right)^2} = 1\) n├¬n c├│ sß╗æ ╬▒ sao cho cos╬▒ = 4/5 v├Ā sin╬▒ = 3/5
Thay v├Āo (1), ta ─æŲ░ß╗Żc :
\(\begin{array}{l}
sin2xcos\alpha - sin\alpha cos2x = 1\\
\Leftrightarrow sin(2x - \alpha ) = 1\\
\Leftrightarrow 2x - \alpha = \frac{\pi }{2} + k2\pi \\
\Leftrightarrow x = \frac{1}{2}\left( {\alpha + \frac{\pi }{2} + k2\pi } \right)(k \in Z)
\end{array}\)
Câu c:
Vß╗øi mß╗Źi x Ōłł R, ta c├│: yŌĆ▓ = ŌłÆ2cosxsinx + cosx = cosx(1 ŌłÆ 2sinx)
\(\begin{array}{l}
y\prime = 0 \Leftrightarrow cosx(1 - 2sinx) = 0 \Leftrightarrow \left[ \begin{array}{l}
cosx = 0\\
1 - 2sinx = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{2} + k\pi \\
sinx = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{6} + k2\pi \\
x = \frac{{5\pi }}{6} + k2\pi
\end{array} \right.
\end{array} \right.
\end{array}\)
Vß║Ły \(x = \frac{\pi }{2} + k\pi ;x = \frac{\pi }{6} + k2\pi ;x = \frac{{5\pi }}{6} + k2\pi (k \in Z)\)
Câu d:
\(\begin{array}{l}
y\prime = \frac{1}{{co{s^2}x}} - \frac{1}{{si{n^2}x}}\forall x \ne k\frac{\pi }{2}\\
y\prime = 0 \Leftrightarrow \frac{1}{{co{s^2}x}} = \frac{1}{{si{n^2}x}} \Leftrightarrow ta{n^2}x = 1\\
\Leftrightarrow tanx = \pm 1 \Leftrightarrow x = \pm \frac{\pi }{4} + k\pi ,k \in Z
\end{array}\)
B├Āi 36 trang 212 SGK To├Īn 11 n├óng cao
Cho h├Ām sß╗æ f(x) = 2cos2(4x ŌłÆ 1). Chß╗®ng minh rß║▒ng vß╗øi mß╗Źi x ta c├│ |fŌĆ▓(x)| Ōēż 8. T├¼m c├Īc gi├Ī trß╗ŗ cß╗¦a x ─æß╗ā ─æß║│ng thß╗®c xß║Ży ra.
HŲ░ß╗øng dß║½n giß║Żi:
Vß╗øi mß╗Źi x Ōłł R, ta c├│:
fŌĆ▓(x) = 2.2cos(4xŌłÆ1).[ŌłÆsin(4xŌłÆ1)]4 = ŌłÆ8sin2(4xŌłÆ1)
Suy ra: |fŌĆ▓(x)| = 8|sin2(4xŌłÆ1)| Ōēż 8
Dß║źu "=" xß║Ży ra khi v├Ā chß╗ē khi:
\(\begin{array}{l}
sin2(4x - 1) = \pm 1\\
\Leftrightarrow 2(4x - 1) = \frac{\pi }{2} + k\pi \\
\Leftrightarrow x = \frac{\pi }{{16}} + \frac{{k\pi }}{8} + \frac{1}{4}\\
\Leftrightarrow x = \frac{1}{{16}}(\pi + 4 + k2\pi )(k \in Z)
\end{array}\)
B├Āi 37 trang 212 SGK To├Īn 11 n├óng cao
Cho mß║Īch ─æiß╗ćn nhŲ░ h├¼nh 5.7. L├║c ─æß║¦u tß╗ź ─æiß╗ćn c├│ ─æiß╗ćn t├Łch Q0. Khi ─æ├│ng kh├│a K, tß╗ź ─æiß╗ćn ph├│ng ─æiß╗ćn qua cuß╗Ön d├óy ; ─æiß╗ćn t├Łch q cß╗¦a tß╗ź ─æiß╗ćn phß╗ź thuß╗Öc v├Āo thß╗Øi gian t theo c├┤ng thß╗®c q(t) = Q0sinŽēt. Trong ─æ├│, Žē l├Ā tß╗æc ─æß╗Ö g├│c. Biß║┐t rß║▒ng cŲ░ß╗Øng ─æß╗Ö I(t) cß╗¦a d├▓ng ─æiß╗ćn tß║Īi thß╗Øi ─æiß╗ām t ─æŲ░ß╗Żc t├Łnh theo c├┤ng thß╗®c I(t) = qŌĆ▓(t) Cho biß║┐t Q0 = 10-8 v├Ā Žē = 106ŽĆrad/s. H├Ży t├Łnh cŲ░ß╗Øng ─æß╗Ö cß╗¦a d├▓ng ─æiß╗ćn tß║Īi thß╗Øi ─æiß╗ām t = 6s (t├Łnh ch├Łnh x├Īc ─æß║┐n 10-5 mA)
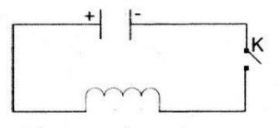
HŲ░ß╗øng dß║½n giß║Żi:
CŲ░ß╗Øng ─æß╗Ö d├▓ng ─æiß╗ćn tß║Īi thß╗Øi ─æiß╗ām t l├Ā :
\(I(t) = q\prime (t) = {Q_0}\omega cos\omega t\)
Khi Q0 = 10-8C v├Ā Žē = 106ŽĆrad/s th├¼ cŲ░ß╗Øng ─æß╗Ö d├▓ng ─æiß╗ćn tß║Īi thß╗Øi ─æiß╗ām t = 6s l├Ā :
\(I(6) = {10^{ - 8}}{.10^{^6}}\pi .cos({10^6}\pi .6) = \frac{\pi }{{100}}(A) \approx 31,41593(mA)\)
B├Āi 38 trang 213 SGK To├Īn 11 n├óng cao
Cho h├Ām sß╗æ y = cos2x + msinx (m l├Ā tham sß╗æ) c├│ ─æß╗ō thß╗ŗ l├Ā (C). T├¼m m trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau:
a. Tiß║┐p tuyß║┐n cß╗¦a (C) tß║Īi ─æiß╗ām vß╗øi ho├Ānh ─æß╗Ö x = ŽĆ c├│ hß╗ć sß╗æ g├│c bß║▒ng 1
b. Hai tiß║┐p tuyß║┐n cß╗¦a (C) tß║Īi c├Īc ─æiß╗ām c├│ ho├Ānh ─æß╗Ö x = ŌłÆŽĆ/4 v├Ā x = ŽĆ/3 song song hoß║Ęc tr├╣ng nhau.
HŲ░ß╗øng dß║½n giß║Żi:
─Éß║Ęt f(x) = cos2x + msinx, ta c├│ :
fŌĆ▓(x) = ŌłÆsin2x + mcosx
Câu a:
Hß╗ć sß╗æ g├│c tiß║┐p tuyß║┐n cß╗¦a (C) tß║Īi ─æiß╗ām c├│ ho├Ānh ─æß╗Ö x = ŽĆ l├Ā:
\(\begin{array}{l}
f\prime (\pi ) = - sin2\pi + mcos\pi = - m\\
\Rightarrow f\prime (\pi ) = 1 \Leftrightarrow m = - 1
\end{array}\)
Câu b:
Theo ─æß╗ü b├Āi ta c├│:
\(f\prime \left( {\frac{{ - \pi }}{4}} \right) = f\prime \left( {\frac{\pi }{3}} \right)\)
\(\begin{array}{l}
\Leftrightarrow - sin\left( {\frac{{ - \pi }}{2}} \right) + mcos\left( {\frac{{ - \pi }}{4}} \right) = - sin\frac{{2\pi }}{3} + mcos\frac{\pi }{3}\\
\Leftrightarrow 1 + m\frac{{\sqrt 2 }}{2} = - \frac{{\sqrt 3 }}{2} + \frac{m}{2} \Leftrightarrow m = \frac{{\sqrt 3 + 2}}{{1 - \sqrt 2 }}
\end{array}\)
Tr├¬n ─æ├óy l├Ā nß╗Öi dung hŲ░ß╗øng dß║½n giß║Żi chi tiß║┐t b├Āi tß║Łp SGK n├óng cao m├┤n To├Īn 11 ChŲ░ŲĪng 5 Luyß╗ćn tß║Łp trang 212 - 213 ─æŲ░ß╗Żc tr├¼nh b├Āy r├Ą r├Āng, cß╗ź thß╗ā vß╗øi phŲ░ŲĪng ph├Īp ngß║»n gß╗Źn v├Ā khoa hß╗Źc. Hy vß╗Źng rß║▒ng ─æ├óy sß║Į l├Ā t├Āi liß╗ću hß╗»u ├Łch gi├║p c├Īc em hß╗Źc sinh lß╗øp 11 hß╗Źc tß║Łp thß║Łt tß╗æt!
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm
















