Đề thi học kỳ 1 môn Toán lớp 12 năm 2017 sau đây gồm trắc nghiệm và tự luận có đáp án sẽ giúp các em học sinh có thêm tài liệu tham khảo chuẩn bị thật tốt cho bài thi học kỳ 1 sắp tới.
|
TRƯỜNG THPT TĨNH GIA 1 ---TỔ TOÁN - TIN--- Mã đề: 101 |
ĐỀ THI HỌC KỲ I-LỚP 12 . NĂM HỌC:2017-2018 Môn thi: Toán học Thời gian: 90 phút (Không kể thời gian phát đề) |
I. CÂU HỎI TRẮC NGHIỆM (8 điểm)
Câu 1: Tìm tập xác định của hàm số \(y = {\left( {x - 2} \right)^{\frac{5}{4}}}\).
A. \(D = R\backslash \left\{ 0 \right\}\) B. \(D = R\) C. \(D = \left( {2; + \infty } \right)\) D. \(D = R\backslash \left\{ 2 \right\}\)
Câu 2: Đồ thị hình bên là đồ thị của một trong bốn hàm số dưới đây. Hỏi đó là hàm số nào?
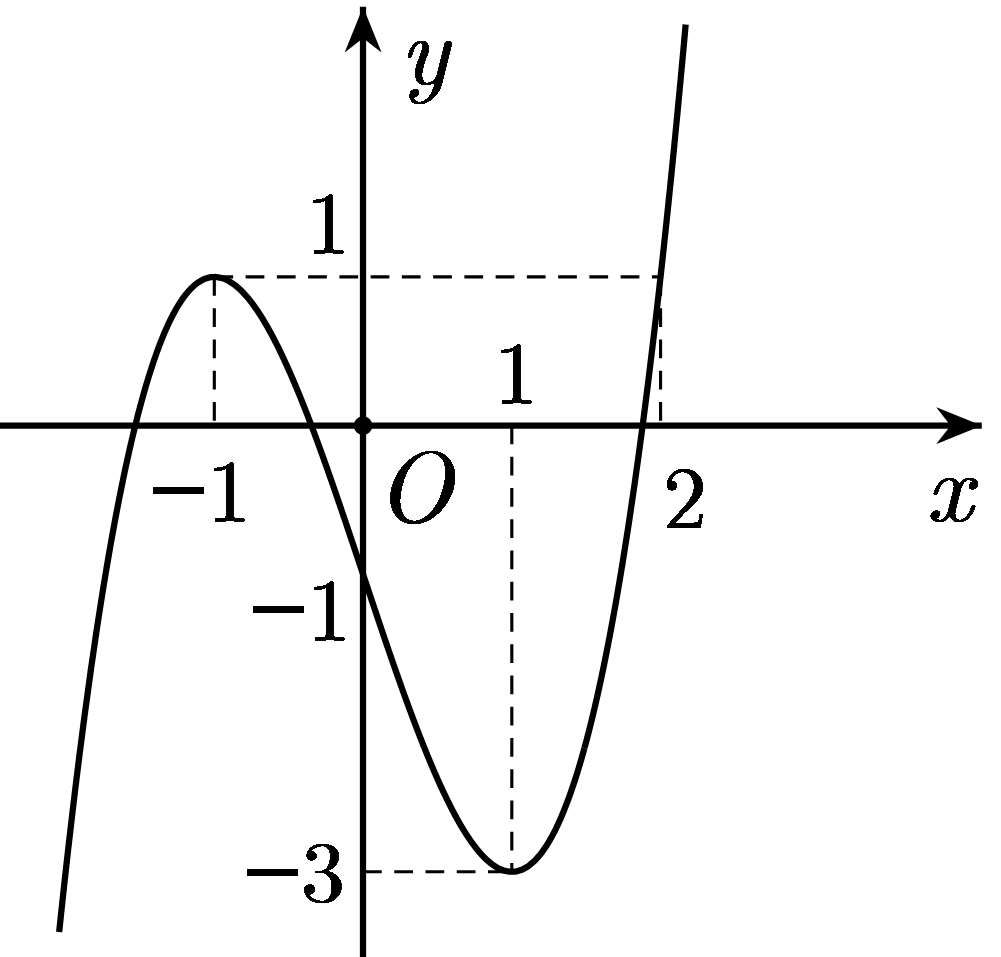
A. \(y = - {x^3} - 3{x^2} - 3x - 1.\)
B. \(y = {x^3} - 3x - 1.\)
C. \(y = - \frac{1}{3}{x^3} + 3x - 1.\)
D. \(y = {x^3} + 3{x^2} - 3x + 1.\)
Câu 3: Tổng các nghiệm của phương trình \({2^{2{x^2} - 7x + 5}} = 1\) bằng
A. 1 B. \(\frac{3}{2}\) C. \(\frac{5}{2}\) D. \(\frac{7}{2}\)
Câu 4: Tập nghiệm S của bất phương trình \({\log _{\frac{1}{2}}}\left( {4 - 3x} \right) < - 4\) là.
A.\(S = \left( { - \infty ; - 4} \right).\) B. \(S = \left( {\frac{4}{3};2} \right).\) C. \(S = \emptyset .\) D. \(S = \left( { - \infty ;\frac{4}{3}} \right).\)
Câu 5: Cho hàm số \(y = - {x^3} + 1\).Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\). B. Hàm số đồng biến trên R.
C. Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\). D. Hàm số nghịch biến trên R.
Câu 6: Diện tích toàn phần của hình nón có bán kính đáy \(R\left( {R > 0} \right)\) và độ dài đường sinh \(l (l > 0)\) là.
A. \({S_{tp}} = 2\pi {R^2} + \pi Rl\). B. \({S_{tp}} = \pi {R^2} + \pi Rl\).
C. \({S_{tp}} = \pi {R^2} + 2\pi Rl\). D. \({S_{tp}} = 2\pi {R^2} + 2\pi Rl\).
Câu 7: Nguyên hàm F(x) của hàm số \(f\left( x \right) = {x^{2017}} + {x^{ - 1}}\) là hàm số nào trong các hàm số dưới đây?
A. \(F(x) = \frac{{{x^{2018}}}}{{2018}} - \frac{1}{{{x^2}}} + C\,\,\,\,\) B. \(F(x) = \frac{{{x^{2018}}}}{{2018}} + \ln \left| x \right|\, + C.\)
C. \(F(x) = 2017.{x^{2016}} + \ln \left| x \right|\,\,\, + C.\) D. \(F(x) = 2017.{x^{2016}} + \ln x\,\,\, + C.\)
Câu 8: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng \(2a{\rm{ }}\left( {a > 0} \right)\) là:
A. \(\frac{{3{\rm{ }}{a^3}}}{2}\). B.\(2\sqrt 3 {\rm{ }}{a^3}\). C. \(\frac{{\sqrt 3 {\rm{ }}{a^3}}}{6}\) . D. \(\frac{{\sqrt 2 {\rm{ }}{a^3}}}{3}\).
Câu 9: Cho \(a > 0,{\rm{ }}a \ne 1\) và x, y là hai số thực thỏa mãn x.y > 0. Khẳng định nào sau đây là khẳng định đúng?
A. \({\log _a}\left( {x.y} \right) = {\log _a}x{\rm{ }}.{\rm{ }}{\log _a}y.\) B. \({\log _a}{x^2} = 2{\log _a}x.\)
C. \({\log _a}\left( {xy} \right) = {\log _a}x + {\log _a}y.\) D. \({\log _a}\left( {xy} \right) = {\log _a}\left| x \right| + {\log _a}\left| y \right|.\)
Câu 10: Số giao điểm của đồ thị hàm số \(y = {x^3} + 3{x^2} + 1.\) và đường thẳng \((d){\rm{ }}:y = 1\) là
A. 0. B. 1. C. 3. D. 2.
----Để xem tiếp nội dung vui lòng xem online hoặc tải về----
Trên đây là phần trích dẫn đề thi học kỳ 1 môn Toán lớp 12. Để xem chi tiết nội dung đề thi, quý thầy cô cùng các em học sinh có thể chọn chức năng xem trực tuyến hoặc tài về máy. Ngoài ra, quý thầy cô và các em học sinh có thể tham khảo thêm một số đề thi khác tại website Hoc247.net







