Đề khảo sát chất lượng đầu năm môn Toán 12 năm 2022 - 2023 có đáp án Trường THPT Phan Đình Phùng nhằm khảo sát chất lượng đầu năm để phân loại học sinh. Thông qua bài khảo sát chất lượng đầu năm, học sinh sẽ xác định rõ năng lực và thái độ học tập của bản thân, qua đó nắm bắt được chính xác tình hình học hiện tại để xác định mục tiêu phù hợp cho năm học mới. HỌC247 mời các em học sinh cùng tham khảo đề thi dưới đây và tải về học tập!
|
TRƯỜNG THPT PHAN ĐÌNH PHÙNG |
ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM HỌC 2022-2023 MÔN: TOÁN 12 Thời gian làm bài: 90 phút; (50 câu trắc nghiệm) |
Câu 1: Tìm tập giá trị của hàm số \(y=\frac{x-1}{x-2}\).
A. \(\left( -\infty \,;\,2 \right)\)
B. \(R\backslash \left\{ 2 \right\}\)
C. \(R\backslash \left\{ 1 \right\}\)
D. \(\left( -\infty \,;\,+\infty \right)\)
Câu 2: Hàm số \(y=\frac{x+1}{x-3}\) có bao nhiêu cực trị:
A. 0
B. 1
C. 2
D. 3
Câu 3: Trong các hàm số sau hàm số nào đồng biến trên R :
A. \(y=\tan x\)
B. \(y={{x}^{3}}+1\)
C. \(y={{x}^{4}}+{{x}^{2}}+1\)
D. \(y=\frac{4x+1}{x+2}\)
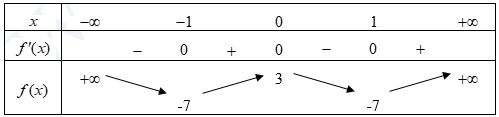
Câu 4: Cho biết hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
Trong các khẳng định sau, khẳng định nào đúng:
A. Hàm số có hai điểm cực đại.
B. Hàm số có hai điểm cực trị.
C. Hàm số có hai điểm cực đại và một điểm cực tiểu.
D. Hàm số có một điểm cực đại và hai điểm cực tiểu.
Câu 5: Hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\,\left( a\ne 0 \right)\) có tối đa bao nhiêu cực trị.
A. 1
B. 2
C. 3
D. 4
Câu 6: Cho biết hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
Giá trị lớn nhất của hàm số \(y=f\left( x \right)\) trên khoảng \(\left( -2\,;\,2 \right)\) là
A. 0
B. -1
C. -7
D. 3
Câu 7: Đồ thị hàm số \(y={{x}^{3}}+2{{x}^{2}}+3x+2017\,\,\) có bao nhiêu đường tiệm cận ngang.
A. 0
B. 1
C. 2
D. 3
Câu 8: Tìm tiệm cận ngang của đồ thị hàm số \(y=\frac{{{x}^{2}}-4\,\,}{{{x}^{3}}+1}\)
A. x=-1
B. y=0
C. x=0
D. y=1
Câu 9: Đồ thị hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\left( a\ne 0 \right)\,\,\) có tất cả bao nhiêu dạng đồ thị
A. 2
B. 3
C. 4
D. 6
Câu 10: Cho đồ thị hàm \(\left( C \right):y=\frac{2x-4}{x-3}\). Trong các khẳng định sau khẳng định nào sai.
A. (C) chỉ có một tiệm cận đứng.
B. (C) chỉ có một tiệm cận ngang.
C. (C) chỉ có một tâm đối xứng.
D. (C) chỉ có một trục đối xứng.
Câu 11: Tính chất nào sau đây không phải là tính chất của hình hộp chữ nhật.
A. Các mặt là hình chữ nhật.
B. Có 16 cạnh
C. Có 8 đỉnh
D. Có 6 mặt
Câu 12: Trong hình đa diện, mỗi cạnh của đa giác là cạnh chung của đúng mấy đa giác.
A. 1
B. 2
C. 3
D. 4
Câu 13: Có tất cả mấy loại khối đa diện đều.
A. 2
B. 3
C. 4
D.5
Câu 14: Khối bát diện đều có bao nhiêu cạnh:
A. 12
B.14
C. 10
D.16
Câu 15: Thể tích khối lập phương có cạnh a là .
A. \(\frac{{{a}^{3}}}{2}\)
B.\(\frac{{{a}^{3}}}{3}\)
C. \(2{{a}^{3}}\)
D.\({{a}^{3}}\)
Câu 16: Thể tích khối chóp có diện tích đáy B và chiều cao h là.
A. \(V=\frac{1}{2}B.H\)
B. \(V=\frac{1}{3}B.H\)
C. \(V=\frac{1}{3}{{B}^{2}}.H\)
D. \(V=B.H\)
Câu 17: Cho hàm số \(y=-2{{x}^{3}}+3{{x}^{2}}+12x-5\). Trong các khẳng định sau, khẳng định nào sai.
A. Hàm số nghịch biến trên khoảng \(\left( -3\,;\,\,-1 \right)\).
B. Hàm số đồng biến trên khoảng \(\left( -1\,;\,\,1 \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( 5\,;\,\,10 \right)\).
D. Hàm số đồng biến trên khoảng \(\left( -1\,;\,\,3 \right)\).
Câu 18: Cho hàm số \(y=\frac{3x+1}{1-x}\). Trong các khẳng định sau, khẳng định nào đúng.
A. Hàm số nghịch biến trên R.
B. Hàm số đồng biến trên R.
C. Hàm số đồng biến trên khoảng \(\left( -\infty \,;\,\,1 \right)\cup \left( 1;+\infty \right)\).
D. Hàm số đồng biến trên khoảng \(\left( -\infty \,;\,\,1 \right)\) và \(\left( 1;+\infty \right)\).
Câu 19: Hàm số \(y=2{{x}^{3}}-3{{x}^{2}}-72x+8\) đạt cực đại tại.
A. x = -3
B. x = 4
C. x = 143
D. x = -200
Câu 20: Hàm số \(y=x{}^{4}-8{{x}^{2}}-6\) có giá trị cực tiểu là.
A. \({{y}_{CT}}=0\)
B. \({{y}_{CT}}=-22\)
C. \({{y}_{CT}}=-6\)
D. \({{y}_{CT}}=2\)
Câu 21: Đồ thị hàm số \(y=\frac{x-2}{{{x}^{2}}-4}\) có bao nhiêu tiệm cận đứng.
A. 0
B. 2
C. 1
D.3
Câu 22: Tìm các tiệm cận ngang của đồ thị hàm số \(y=\frac{2\sqrt{{{x}^{2}}-1}+1}{x}\).
A. y = 2
B. y = -2
C. \(y=2\,\,;\,y=-2\)
D. \(x=2\,\,;\,x=-2\)
Câu 23: Tìm giá trị lớn nhất của hàm số \(y=-2{{x}^{2}}+8x+1\).
A. 2
B. 9
C. \(+\infty \)
D.0
Câu 24: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x+35\) trên đoạn \(\left[ -4\,\,;\,4 \right]\).
A. \(Max=40\,\,;\,\,Min=-41\)
B. \(Max=15\,\,;\,\,Min=-41\)
C. \(Max=40\,\,;\,\,Min=8\)
D. \(Max=40\,\,;\,\,Min=15\)
Câu 25: Tìm tâm đối xứng của đồ thị hàm số \(y=\frac{{{x}^{3}}}{3}-2{{x}^{2}}+3x+1\).
A. \(\left( 2\,;\,0 \right)\)
B. \(\left( 2\,;\,\frac{5}{3} \right)\)
C. \(\left( 1\,;\,\frac{7}{3} \right)\)
D. \(\left( 3\,;\,1 \right)\)
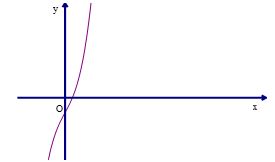
Câu 26: Đồ thị hình bên là của hàm số:
A. \(y={{x}^{3}}+2x-1\)
B. \(y=-{{x}^{3}}-2x+1\)
C. \(y={{x}^{3}}-3x-1\)
D. \(y=-{{x}^{3}}-3x+1\)
Câu 27: Khối lập phương thuộc loại khối đa diện đều nào.
A. \(\left\{ 3\,\,;\,\,4 \right\}\)
B. \(\left\{ 5\,\,;\,\,3 \right\}\)
C. \(\left\{ 4\,;\,\,3 \right\}\)
D. \(\left\{ 3\,;5 \right\}\)
Câu 28: Điểm trong của khối lăng trụ là điểm.
A. Không thuộc khối lăng trụ.
B. Thuộc khối lăng trụ và thuộc hình lăng trụ.
C. Thuộc hình lăng trụ.
D. Thuộc khối lăng trụ nhưng không thuộc hình lăng trụ.
Câu 29: Trong không gian, phép biến hình nào sao đây không phải là phép dời hình.
A. Phép đối xứng qua đường thẳng \(\Delta \).
B. Phép vị tự tỉ số k=-3
C. Phép tịnh tiến theo vectơ \(\overrightarrow{v}\).
D. Phép đối xứng tâm O.
Câu 30: Trong khối đa diện đều loại \(\left\{ 5\,\,;\,\,3 \right\}\). Mỗi đỉnh của nó là đỉnh chung của mấy mặt.
A. 3
B. 4
C. 5
D. 6
Câu 31: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng 2a và chiều cao của khối chóp là \(\frac{a\sqrt{2}}{3}\). Tính theo a thể tích của khối chóp S.ABC.
A. \(\frac{{{a}^{3}}\sqrt{6}}{18}\)
B. \(\frac{{{a}^{3}}\sqrt{6}}{9}\)
C. \(\frac{{{a}^{3}}\sqrt{6}}{3}\)
D. \(\frac{{{a}^{3}}\sqrt{6}}{6}\)
Câu 32: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật , \(SA\bot \left( ABCD \right)\), \(AC=2a\,;\,\,AB=a\,\,;\,\,SD=a\sqrt{5}\). Tính theo a thể tích của khối chóp S.ABCD.
A. \(\frac{{{a}^{3}}\sqrt{5}}{3}\)
B. \(\frac{{{a}^{3}}\sqrt{15}}{3}\)
C. \({{a}^{3}}\sqrt{6}\)
D. \(\frac{{{a}^{3}}\sqrt{6}}{3}\)
Câu 33: Cho hàm số \(y=\sqrt{4x-{{x}^{2}}}\). Khẳng định nào sau đây là khẳng định đúng.
A. Hàm số đồng biến trên khoảng \(\left( -\infty \,\,;\,\,2 \right)\) và nghịch biến trên khoảng \(\left( 2\,\,;\,+\,\infty \right)\).
B. Hàm số đồng biến trên khoảng \(\left( 0\,\,;\,\,2 \right)\) và nghịch biến trên khoảng \(\left( 2\,\,;\,4 \right)\).
C. Hàm số đồng biến trên khoảng \(\left( -\infty \,\,;\,\,0 \right)\) và nghịch biến trên khoảng \(\left( 4\,\,;\,+\,\infty \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( 0\,\,;\,\,2 \right)\) và đồng biến trên khoảng \(\left( 2\,\,;\,4 \right)\).
Câu 34: Tìm tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{3}{{x}^{3}}+2{{x}^{2}}-mx-10\) đồng biến trên R.
A. \(m\ge -4\)
B. \(m>-4\)
C. \(m\le -4\)
D. \(m<-4\)
Câu 35: Tìm tất cả các giá trị số m để hàm số \(y={{x}^{3}}+3{{x}^{2}}+mx+m-2\) có cực đại và cực tiểu.
A. \(m>3\)
B. \(m\ge 3 \)
C. \(m<3 \)
D. \(m\le 3\)
Câu 36: Tìm tất cả các giá trị số m để hàm số \(y={{x}^{3}}-m{{x}^{2}}+m-1\) đạt cực đại tại x=-2.
A. m=-3
B. m=-2
C. m=3
D. m=2
Câu 37: Tìm giá trị nhỏ nhất của hàm số \(y=x+\frac{1}{x-1}\) trên khoảng \(\left( 1\,\,;\,+\,\infty \right)\).
A. Min=2
B. Min=3
C. Min=4
D. Min=0
Câu 38 : Tìm giá trị lớn nhất của hàm số \(y=\cos 2x+2\operatorname{sinx}-3\) trên \(\left[ \frac{-\pi }{6};\frac{5\pi }{6} \right]\)
A. \(Max=\frac{-3}{2}\)
B. \(Max=\frac{-7}{2}\)
C. \(Max=\frac{3}{2}\)
D. \(Max=\frac{7}{2}\)
Câu 39: Viết phương trình đường thẳng đi qua hai điểm cực tiểu của hàm số \(y={{x}^{4}}-4{{x}^{2}}+1\).
A. x=-3
B. y=1
C. x=1
D. y=-3
Câu 40: Tìm tất cả các giá trị số m để đồ thị hàm số \(y=\frac{2x-m}{x+m}\) đối xứng qua điểm có tọa độ \(\left( 1\,\,;\,2 \right)\).
A. m=2
B. m=1
C. m=-1
D. m=-2
Câu 41: Cho khối chóp tam giác S.ABC có cạnh đáy là tam giác vuông tại A , \(AC=a\,\,,\,BC=2a\). Hình chiếu của S trên (ABC) là trung điểm H của BC. Cạnh bên SB tạo với đáy một góc \({{60}^{o}}\).Tính theo a thể tích của khối chóp S.ABC.
A. \(\frac{{{a}^{3}}}{6}\)
B. \(\frac{{{a}^{3}}\sqrt{3}}{12}\)
C. \(\frac{{{a}^{3}}\sqrt{3}}{5}\)
D. \(\frac{{{a}^{3}}}{2}\)
Câu 42: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng \(a\sqrt{3}\) và các mặt bên là các tam giác vuông cân tại S. Tính theo a thể tích của khối chóp S.ABC.
A. \(\frac{{{a}^{3}}\sqrt{21}}{6}\)
B. \(\frac{{{a}^{3}}\sqrt{21}}{12}\)
C. \(\frac{{{a}^{3}}\sqrt{6}}{8}\)
D. \(\frac{{{a}^{3}}\sqrt{6}}{4}\)
Câu 43: Tìm tất cả các giá trị số m để đồ thị hàm số \(y=\frac{x-1}{x-m}\) nghịch biến trên khoảng \(\left( -\infty \,;\,3 \right)\).
A. m>1
B. \(m\ge 1\)
C. m > 3
D. \(m\ge 3\)
Câu 44: Tìm tất cả các giá trị số m để đồ thị hàm số \(y=\frac{{{x}^{2}}+x-2}{{{x}^{2}}-2x+m}\) có hai đường tiệm cận đứng phân biệt.
A. \(m\in \left( -\infty \,\,;\,1 \right)\)
B. \(m\in \left( -\infty \,\,;\,-8 \right)\cup \left( -8\,\,;\,\,1 \right)\)
C. \(m\in \left( -\infty \,\,;\,-1 \right)\)
D. \(m\in \left( -8\,\,;\,1 \right)\)
Câu 45: Tìm tất cả các giá trị số m để đồ thị hàm số \(y=2{{x}^{3}}+3\left( m-1 \right){{x}^{2}}+6\left( m-2 \right)x-2017\) có hai điểm cực trị nằm trong khoảng \(\left( -5\,;\,5 \right)\).
A. -3 < m
B. m < 7
C. -3 < m < 7
D. 7 < m < 11
Câu 46: Tìm tất cả các giá trị số m để \(\underset{-1\le x\le 1}{\mathop{Min}}\,\left( -{{x}^{3}}-3{{x}^{2}}+m \right)=0\).
A. m=-4
B. m=2
C. m=0
D. m=4
Câu 47: Tìm tất cả các giá trị số m để đồ thị hàm số \(y={{x}^{3}}-2{{x}^{2}}+\left( 1-m \right)x+m\) cắt trục hoành tại ba điểm phân biệt có hoành độ \({{x}_{1}}\,,\,{{x}_{2}}\,,\,{{x}_{3}}\) thõa mãn điều kiện \(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}<4\).
A. \(m\in \left( \frac{1}{4}\,;\,0 \right)\)
B. \(m\in \left( 0\,\,;\,\,1 \right)\)
C. \(m\in \left( -\frac{1}{4}\,\,;\,0 \right)\cup \left( 0\,\,;1 \right)\)
D. m=0
Câu 48: Hình chóp S. ABC có \(SA=SB=SC=\frac{\sqrt{42}}{3}\), đáy là tam giác ABC có \(AB=1\,\,,\,\,AC=2,\,\,\widehat{BAC}={{120}^{o}}\). Tính thể tích khối chóp.
A. \(V=\frac{\sqrt{7}}{6}\)
B. \(V=\frac{\sqrt{6}}{7}\)
C. \(V=\frac{\sqrt{2}}{3}\)
D. \(V=\frac{\sqrt{2}}{4}\)
Câu 49: Hình chóp S.ABC có \(SA=SB=SC\), đáy tam giác ABC vuông tại A có \(AB=1\,\,,\,\,AC=2,\,\) góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) bằng \({{60}^{o}}\). Tính thể tích khối chóp.
A. \(V=\frac{\sqrt{3}}{3}\)
B. \(V=\frac{\sqrt{3}}{2}\)
C. \(V=\frac{\sqrt{3}}{4}\)
D. \(V=\sqrt{3}\)
Câu 50: Xét khối chóp tứ giác S.ABCD, trong đó SBAC là tứ diện đều cạnh a và ABCD là hình thoi. Tính thể tích khối chóp đó.
A. \(\frac{{{a}^{3}}\sqrt{2}}{2}\)
B. \(\frac{{{a}^{3}}\sqrt{2}}{3}\)
C. \(\frac{{{a}^{3}}\sqrt{2}}{6}\)
D. \(\frac{{{a}^{3}}\sqrt{2}}{12}\)
ĐÁP ÁN
|
CÂU |
ĐÁP ÁN |
CÂU |
ĐÁP ÁN |
|
1 |
C |
26 |
A |
|
2 |
A |
27 |
C |
|
3 |
B |
28 |
D |
|
4 |
D |
29 |
B |
|
5 |
B |
30 |
A |
|
6 |
D |
31 |
B |
|
7 |
A |
32 |
D |
|
8 |
B |
33 |
B |
|
9 |
C |
34 |
C |
|
10 |
D |
35 |
C |
|
11 |
B |
36 |
A |
|
12 |
B |
37 |
B |
|
13 |
D |
38 |
A |
|
14 |
A |
39 |
D |
|
15 |
D |
40 |
C |
|
16 |
B |
41 |
D |
|
17 |
D |
42 |
C |
|
18 |
D |
43 |
D |
|
19 |
A |
44 |
B |
|
20 |
B |
45 |
C |
|
21 |
C |
46 |
D |
|
22 |
C |
47 |
C |
|
23 |
B |
48 |
A |
|
24 |
A |
49 |
A |
|
25 |
B |
50 |
C |
Trên đây là một phần trích đoạn nội dung Đề khảo sát chất lượng đầu năm môn Toán 12 năm 2022 - 2023 có đáp án Trường THPT Phan Đình Phùng. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Mời các em tham khảo tài liệu có liên quan:
Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.