Hß╗īC247 xin chia sß║╗ t├Āi liß╗ću nß╗Öi dung Bß╗Ö 5 ─æß╗ü thi thß╗Ł THPT QG m├┤n To├Īn n─ām 2021-2022 TrŲ░ß╗Øng THPT Nguyß╗ģn Huß╗ć c├│ ─æ├Īp ├Īn ─æß║¦y ─æß╗¦ trong nß╗Öi dung b├Āi viß║┐t dŲ░ß╗øi ─æ├óy. Th├┤ng qua nß╗Öi dung t├Āi liß╗ću, c├Īc em sß║Į h├¼nh dung ─æŲ░ß╗Żc nß╗Öi dung trß╗Źng t├óm m├Ā m├¼nh cß║¦n ├┤n lß║Īi v├Ā l├Ām quen vß╗øi nhß╗»ng dß║Īng c├óu hß╗Åi c├│ thß╗ā xuß║źt hiß╗ćn trong k├¼ thi THPT QG n─ām 2022. Mong rß║▒ng t├Āi liß╗ću sß║Į gi├║p c├Īc em cß║¦n ├┤n tß║Łp kiß║┐n thß╗®c thß║Łt chß║»c ─æß╗ā chuß║®n bß╗ŗ thß║Łt tß╗æt cho c├Īc kß╗│ thi sß║»p tß╗øi.
|
TRŲ»ß╗£NG THPT NGUYß╗äN HUß╗å |
─Éß╗Ć THI THß╗¼ THPT QUß╗ÉC GIA M├öN TO├üN N─éM Hß╗īC 2021 ŌĆō 2022 Thß╗Øi gian: 90 ph├║t |
─Éß╗Ć Sß╗É 1
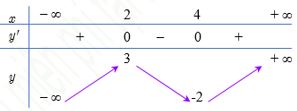
C├óu 1.Cho h├Ām sß╗æ \(f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ sau:
.jpg?enablejsapi=1)
H├Ām sß╗æ ─æ├Ż cho nghß╗ŗch biß║┐n tr├¬n khoß║Żng n├Āo dŲ░ß╗øi ─æ├óy?
A. \(\left( -1\,;\text{3} \right)\).
B. \(\left( -\infty \,;-1 \right)\).
C. \(\left( -1\,;\text{1} \right)\).
D. \(\left( -1\,;\text{2} \right)\).
C├óu 2.Cho cß║źp sß╗æ nh├ón \(\left( {{u}_{n}} \right)\) c├│ \({{u}_{1}}=2\) v├Ā c├┤ng bß╗Öi q = 6. Gi├Ī trß╗ŗ cß╗¦a \({{u}_{2}}\) bß║▒ng
A. 8.
B. 36.
C. 3.
D. 12.
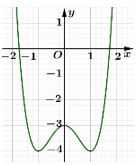
C├óu 3.─ÉŲ░ß╗Øng cong trong h├¼nh vß║Į b├¬n l├Ā ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ n├Āo dŲ░ß╗øi ─æ├óy?
.jpg)
A. \(y=\frac{x+1}{2x-2}\).
B. \(y={{x}^{3}}-3x+2\).
C. \(y={{x}^{4}}-2{{x}^{2}}-3\).
D. \(y=-{{x}^{3}}+3x-1\).
C├óu 4.Vß╗øi a l├Ā sß╗æ thß╗▒c dŲ░ŲĪng v├Ā \(a\ne 1\), khi ─æ├│ \({{\log }_{a}}\left( {{a}^{2}} \right)\) bß║▒ng
A. 3.
B. a.
C. 2.
D. 1.
C├óu 5.Biß║┐t \(\int\limits_{1}^{5}{f(x)\text{d}x=6,\,\,\,}\int\limits_{1}^{5}{g(x)\text{d}x=-2\,}\). Gi├Ī trß╗ŗ cß╗¦a \(\int\limits_{1}^{5}{\left[ f(x)-g(x) \right]\text{d}x}\) bß║▒ng
A. 8.
B. -12.
C. -3.
D. 4.
C├óu 6.Tiß╗ćm cß║Łn ─æß╗®ng cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=\frac{x+2}{x-2}\) l├Ā ─æŲ░ß╗Øng thß║│ng
A. y=2.
B. y=1.
C. x=2.
D. x=-2.
C├óu 7.Sß╗æ giao ─æiß╗ām cß╗¦a hai ─æß╗ō thß╗ŗ \(y={{x}^{3}}-2x+1\) v├Ā \(y={{x}^{2}}+x+1\) l├Ā
A. 2.
B. 1.
C. 4.
D. 3.
C├óu 8.─Éß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y={{2021}^{x}}\) l├Ā
A. \({{y}^{'}}=\frac{{{2021}^{x}}}{\ln 2021}\).
B. \({{y}^{'}}={{2021}^{x}}\ln 2021\).
C. \({{y}^{'}}=x{{.2021}^{x}}\).
D. \({{y}^{'}}={{2021}^{x}}\).
C├óu 9.Cho a l├Ā sß╗æ thß╗▒c dŲ░ŲĪng t├╣y ├Į, viß║┐t biß╗āu thß╗®c \(\frac{\sqrt[3]{{{a}^{2}}}}{{{a}^{3}}}\) vß╗ü dß║Īng luß╗╣ thß╗½a cß╗¦a a l├Ā
A. \({{a}^{2}}\).
B. \({{a}^{-\frac{7}{3}}}\).
C. \({{a}^{\frac{2}{9}}}\).
D. \({{a}^{\frac{11}{3}}}\).
C├óu 10.Trong c├Īc sß╗æ phß╗®c sau, sß╗æ phß╗®c n├Āo l├Ā sß╗æ thuß║¦n ß║Żo?
A. \(z=4\).
B. \(z=-3+\sqrt{3}i\).
C. \(z=2-i\).
D. \(z=-i\).
---(─Éß╗ā xem tiß║┐p nß╗Öi dung tß╗½ c├óu 11 ─æß║┐n c├óu 50 cß╗¦a ─æß╗ü thi sß╗æ 1 c├Īc em vui l├▓ng xem Online hoß║Ęc ─É─āng nhß║Łp v├Āo HOC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 2
─Éß╗Ć THI THß╗¼ THPT QG M├öN TO├üN TRŲ»ß╗£NG THPT NGUYß╗äN HUß╗å- ─Éß╗Ć 02
C├óu 1: Cho tß║Łp hß╗Żp \(S=\left\{ 1;3;5;7;9 \right\}\). C├│ bao nhi├¬u sß╗æ tß╗▒ nhi├¬n gß╗ōm ba chß╗» sß╗æ kh├Īc nhau ─æŲ░ß╗Żc lß║Łp tß╗½ c├Īc phß║¦n tß╗Ł cß╗¦a tß║Łp S?
A. 3!.
B. \({{3}^{5}}\).
C. \(C_{5}^{3}\).
D. \(A_{5}^{3}\).
C├óu 2:Cho mß╗Öt d├Ży cß║źp sß╗æ nh├ón \(\left( {{u}_{n}} \right)\) c├│ \({{u}_{1}}=\frac{1}{2}\) v├Ā \({{u}_{2}}=2\). Gi├Ī trß╗ŗ cß╗¦a \({{u}_{4}}\) bß║▒ng
A. 32.
B. 6.
C. \(\frac{1}{32}\).
D. \(\frac{25}{2}\).
C├óu 3: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n sau:
Khß║│ng ─æß╗ŗnh n├Āo sau ─æ├óy sai?
A. H├Ām sß╗æ \(y=f\left( x \right)\) ─æß╗ōng biß║┐n tr├¬n khoß║Żng \(\left( -\infty ;-2 \right)\).
B. H├Ām sß╗æ nghß╗ŗch biß║┐n tr├¬n khoß║Żng \(\left( -2;2 \right)\).
C. H├Ām sß╗æ nghß╗ŗch biß║┐n tr├¬n khoß║Żng \(\left( -2;0 \right)\).
D. H├Ām sß╗æ ─æß╗ōng biß║┐n ─æiß╗ću tr├¬n \(\left( 0;2 \right)\).
C├óu 4: H├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ sau:
T├¼m khß║│ng ─æß╗ŗnh ─æ├║ng?
A. H├Ām sß╗æ c├│ ba ─æiß╗ām cß╗▒c trß╗ŗ.
B. H├Ām sß╗æ c├│ gi├Ī trß╗ŗ cß╗▒c ─æß║Īi l├Ā x = -1.
C. H├Ām sß╗æ ─æß║Īt cß╗▒c ─æß║Īi tß║Īi x = 0.
D. H├Ām sß╗æ c├│ ─æiß╗ām cß╗▒c tiß╗āu l├Ā x = 1.
C├óu 5: Cho h├Ām sß╗æ \(y=f\left( x \right)\) li├¬n tß╗źc tr├¬n \(\mathbb{R}\) v├Ā c├│ bß║Żng x├®t dß║źu cß╗¦a \({f}'\left( x \right)\) nhŲ░ sau:
H├Ām sß╗æ \(f\left( x \right)\) c├│ bao nhi├¬u ─æiß╗ām cß╗▒c trß╗ŗ?
A. 2.
B. 3.
C. 0.
D. 1.
C├óu 6: Cho h├Ām sß╗æ \(y=\frac{2x+1}{x-1}\). Tiß╗ćm cß║Łn ─æß╗®ng cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ l├Ā
A. ─ÉŲ░ß╗Øng thß║│ng x=1.
B. ─ÉŲ░ß╗Øng thß║│ng x=2.
C. ─ÉŲ░ß╗Øng thß║│ng y=2.
D. ─ÉŲ░ß╗Øng thß║│ng y=1.
C├óu 7: Cho h├Ām sß╗æ c├│ ─æß╗ō thß╗ŗ nhŲ░ h├¼nh vß║Į:
H├Ām sß╗æ n├Āo dŲ░ß╗øi ─æ├óy c├│ ─æß╗ō thß╗ŗ l├Ā h├¼nh vß║Į tr├¬n?
A. \(y={{x}^{4}}-4{{x}^{2}}+2\).
B. \(y={{x}^{3}}-3x+2\).
C. \(y=-{{x}^{4}}+4{{x}^{2}}+2\).
D. \(y=-{{x}^{3}}+3x+2\).
C├óu 8: ─Éß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y=\left( {{x}^{2}}-2 \right)\left( {{x}^{2}}+2 \right)\) cß║»t trß╗źc tung tß║Īi ─æiß╗ām c├│ tß╗Źa ─æß╗Ö l├Ā
A. \(\left( 0;4 \right)\).
B. \(\left( 0;-4 \right)\).
C. \(\left( 4;0 \right)\).
D. \(\left( -4;0 \right)\).
C├óu 9: Vß╗øi a l├Ā sß╗æ thß╗▒c dŲ░ŲĪng t├╣y ├Į, \(\ln \left( e{{a}^{\pi }} \right)\) bß║▒ng
A. \(1+a\ln \pi \).
B. \(1-\pi \ln a\).
C. \(1+\pi \ln a\).
D. \(1+\ln \pi +\ln a\).
C├óu 10: ─Éß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y={{\pi }^{x}}\) l├Ā
A. \(x{{\pi }^{x-1}}\).
B. \(\frac{{{\pi }^{x}}}{\ln \pi }\).
C. \({{\pi }^{x}}\).
D. \({{\pi }^{x}}\ln \pi \).
---(─Éß╗ā xem tiß║┐p nß╗Öi dung tß╗½ c├óu 11 ─æß║┐n c├óu 50 cß╗¦a ─æß╗ü thi sß╗æ 2 c├Īc em vui l├▓ng xem Online hoß║Ęc ─É─āng nhß║Łp v├Āo HOC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 3
─Éß╗Ć THI THß╗¼ THPT QG M├öN TO├üN TRŲ»ß╗£NG THPT NGUYß╗äN HUß╗å- ─Éß╗Ć 03
C├óu 1: C├│ bao nhi├¬u sß╗æ tß╗▒ nhi├¬n c├│ ba chß╗» sß╗æ ─æ├┤i mß╗Öt kh├Īc nhau?
A. \(C_{10}^{3}\).
B. \({{3}^{10}}\).
C. \(A_{10}^{3}\).
D. \(9.A_{9}^{2}\).
C├óu 2: Cho cß║źp sß╗æ cß╗Öng \(\left( {{u}_{n}} \right)\), biß║┐t \({{u}_{1}}=6\) v├Ā \({{u}_{3}}=-2\). Gi├Ī trß╗ŗ cß╗¦a \({{u}_{8}}\) bß║▒ng
A. -8.
B. 22.
C. 34.
D. -22.
C├óu 3: Cho h├Ām sß╗æ \(y=f\left( x \right)\) x├Īc ─æß╗ŗnh v├Ā li├¬n tß╗źc tr├¬n khoß║Żng \(\left( -\infty ;+\infty \right),\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ h├¼nh sau:
H├Ām sß╗æ ─æ├Ż cho nghß╗ŗch biß║┐n tr├¬n khoß║Żng n├Āo dŲ░ß╗øi ─æ├óy?
A. \(\left( -1;0 \right).\)
B. \(\left( 0;1 \right)\).
C. \(\left( -1;4 \right)\).
D. \(\left( 1;+\infty \right)\).
C├óu 4: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ sau
H├Ām sß╗æ \(f\left( x \right)\) ─æß║Īt cß╗▒c ─æß║Īi tß║Īi ─æiß╗ām
A. x = 2.
B. x = -5.
C. x = 3.
D. x = 0.
C├óu 5: Cho h├Ām sß╗æ \(y=f\left( x \right)\) li├¬n tß╗źc tr├¬n \(\mathbb{R}\) v├Ā c├│ bß║Żng x├®t dß║źu ─æß║Īo h├Ām dŲ░ß╗øi ─æ├óy.
Sß╗æ ─æiß╗ām cß╗▒c trß╗ŗ cß╗¦a h├Ām sß╗æ l├Ā
A. 1.
B. 0.
C. 2.
D. 3.
C├óu 6: Sß╗æ ─æŲ░ß╗Øng tiß╗ćm cß║Łn cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=\frac{5x+3}{2x-1}\) l├Ā
A. 3.
B. 0.
C. 2.
D. 1.
C├óu 7: ─Éß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ n├Āo dŲ░ß╗øi ─æ├óy c├│ dß║Īng nhŲ░ ─æŲ░ß╗Øng cong trong h├¼nh b├¬n:
A. \(y=-{{x}^{3}}+3x+2\).
B. \(y={{x}^{4}}-{{x}^{2}}+2\).
C. \(y=-{{x}^{2}}+x-2\).
D. \(y={{x}^{3}}-3x+2\).
C├óu 8: ─Éß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y=\frac{x-3}{2x-1}\) cß║»t trß╗źc ho├Ānh tß║Īi ─æiß╗ām c├│ ho├Ānh ─æß╗Ö bß║▒ng
A. - 2.
B. \(\frac{1}{2}\).
C. 3.
D. - 3.
C├óu 9: Vß╗øi a l├Ā sß╗æ thß╗▒c dŲ░ŲĪng t├╣y ├Į, \({{\log }_{5}}\left( \frac{125}{a} \right)\) bß║▒ng
A. \(3+{{\log }_{5}}a\).
B. \(3{{\log }_{5}}a\).
C. \({{\left( {{\log }_{5}}a \right)}^{3}}\).
D. \(3-{{\log }_{5}}a\).
C├óu 10: Vß╗øi x > 0, ─æß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y={{\log }_{2}}x\) l├Ā
A. \(\frac{x}{\ln 2}\).
B. \(\frac{1}{x.\ln 2}\).
C. \(x.\ln 2\).
D. \({{2}^{x}}.\ln 2\).
---(─Éß╗ā xem tiß║┐p nß╗Öi dung tß╗½ c├óu 11 ─æß║┐n c├óu 50 cß╗¦a ─æß╗ü thi sß╗æ 3 c├Īc em vui l├▓ng xem Online hoß║Ęc ─É─āng nhß║Łp v├Āo HOC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 4
─Éß╗Ć THI THß╗¼ THPT QG M├öN TO├üN TRŲ»ß╗£NG THPT NGUYß╗äN HUß╗å- ─Éß╗Ć 04
C├óu 1: C├│ 5 ngŲ░ß╗Øi ─æß║┐n nghe mß╗Öt buß╗Ģi h├▓a nhß║Īc. Sß╗æ c├Īch xß║┐p 5 ngŲ░ß╗Øi n├Āy v├Āo mß╗Öt h├Āng c├│ 5 ghß║┐ l├Ā:
A. 130.
B. 125.
C. 120.
D. 100.
C├óu 2: Cho cß║źp sß╗æ nh├ón \(\left( {{u}_{n}} \right)\) vß╗øi \({{u}_{1}}=-\frac{1}{2};\text{ }{{u}_{7}}=-32\). T├¼m q?
A. \(q=\pm 2\).
B. \(q=\pm 4\).
C. \(q=\pm 1\).
D. \(q=\pm \frac{1}{2}\).
C├óu 3: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ sau:
H├Ām sß╗æ \(y=f\left( x \right)\) nghß╗ŗch biß║┐n tr├¬n khoß║Żng n├Āo dŲ░ß╗øi ─æ├óy?
A. \(\left( -\infty ;0 \right)\).
B. \(\left( -\infty ;-2 \right)\).
C. \(\left( -1;0 \right)\).
D. \(\left( 0;+\infty \right)\).
C├óu 4: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ h├¼nh b├¬n:
Khß║│ng ─æß╗ŗnh n├Āo sau ─æ├óy l├Ā ─æ├║ng?
A. H├Ām sß╗æ ─æß║Īt cß╗▒c ─æß║Īi tß║Īi x=3.
B. H├Ām sß╗æ ─æß║Īt cß╗▒c ─æß║Īi tß║Īi x=4.
C. H├Ām sß╗æ ─æß║Īt cß╗▒c ─æß║Īi tß║Īi x=2.
D. H├Ām sß╗æ ─æß║Īt cß╗▒c ─æß║Īi tß║Īi x=-2.
C├óu 5: Cho h├Ām sß╗æ y=f(x) li├¬n tß╗źc tr├¬n \(\mathbb{R}\)v├Ā c├│ bß║Żng x├®t dß║źu \({f}'\left( x \right)\) nhŲ░ sau:
Kß║┐t luß║Łn n├Āo sau ─æ├óy ─æ├║ng
A. H├Ām sß╗æ c├│ 4 ─æiß╗ām cß╗▒c trß╗ŗ.
B. H├Ām sß╗æ c├│ 2 ─æiß╗ām cß╗▒c ─æß║Īi.
C. H├Ām sß╗æ c├│ 2 ─æiß╗ām cß╗▒c trß╗ŗ.
D. H├Ām sß╗æ c├│ 2 ─æiß╗ām cß╗▒c tiß╗āu.
C├óu 6: ─ÉŲ░ß╗Øng thß║│ng n├Āo dŲ░ß╗øi ─æ├óy l├Ā tiß╗ćm cß║Łn ngang cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=\frac{1-4x}{2x-1}\).
A. y=2.
B. y=4.
C. \(y=\frac{1}{2}\).
D. y=-2.
C├óu 7: ─ÉŲ░ß╗Øng cong trong h├¼nh vß║Į b├¬n l├Ā ─æß╗ō thß╗ŗ cß╗¦a mß╗Öt h├Ām sß╗æ trong bß╗æn h├Ām sß╗æ ─æŲ░ß╗Żc liß╗ćt k├¬ ß╗¤ bß╗æn phŲ░ŲĪng ├Īn A, B, C, D dŲ░ß╗øi ─æ├óy. Hß╗Åi ─æ├│ l├Ā h├Ām sß╗æ n├Āo?
A. \(y=-{{x}^{3}}+{{x}^{2}}-2\).
B. \(y=-{{x}^{4}}+3{{x}^{2}}-2\).
C. \(y={{x}^{4}}-2{{x}^{2}}-3\).
D. \(y=-{{x}^{2}}+x-1\).
C├óu 8: ─Éß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y=-{{x}^{4}}-3{{x}^{2}}+1\) cß║»t trß╗źc tung tß║Īi ─æiß╗ām c├│ tung ─æß╗Ö bß║▒ng
A. -3.
B. 0.
C. 1.
D. -1.
C├óu 9: Cho a > 0, \(a\ne 1\). T├Łnh \({{\log }_{a}}\left( {{a}^{2}} \right)\).
A. 2a.
B. -2.
C. 2.
D. a.
C├óu 10: ─Éß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y={{3}^{x}}\) l├Ā
A. \({y}'=x\ln 3\).
B. \({y}'=x{{.3}^{x-1}}\).
C. \({y}'=\frac{{{3}^{x}}}{\ln 3}\).
D. \({y}'={{3}^{x}}\ln 3\).
---(─Éß╗ā xem tiß║┐p nß╗Öi dung tß╗½ c├óu 11 ─æß║┐n c├óu 50 cß╗¦a ─æß╗ü thi sß╗æ 4 c├Īc em vui l├▓ng xem Online hoß║Ęc ─É─āng nhß║Łp v├Āo HOC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 5
─Éß╗Ć THI THß╗¼ THPT QG M├öN TO├üN TRŲ»ß╗£NG THPT NGUYß╗äN HUß╗å- ─Éß╗Ć 05
C├óu 1: C├│ bao nhi├¬u c├Īch sß║»p xß║┐p 5 hß╗Źc sinh ─æß╗®ng th├Ānh mß╗Öt h├Āng dß╗Źc?
A. 5!
B. \({{5}^{3}}\)
C. \(C_{5}^{5}\)
D. \(A_{5}^{1}\)
C├óu 2: Cho cß║źp sß╗æ nh├ón \(\left( u_{n}^{{}} \right)\) c├│ \(u_{1}^{{}}=2\) v├Ā c├┤ng bß╗Öi q = -3. Gi├Ī trß╗ŗ cß╗¦a \(u_{3}^{{}}\) l├Ā:
A. -6
B. -18
C. 18
D. -4
C├óu 3: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ sau:
H├Ām sß╗æ ─æ├Ż cho nghß╗ŗch biß║┐n tr├¬n khoß║Żng n├Āo trong c├Īc khoß║Żng dŲ░ß╗øi ─æ├óy?
A. \(\left( -2;0 \right)\).
B. \(\left( -2;-1 \right)\).
C. \(\left( 3;+\infty \right)\).
D. \(\left( -1;+\infty \right)\).
C├óu 4: Cho h├Ām sß╗æ bß║Łc ba \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\left( a\ne 0 \right)\) c├│ ─æß╗ō thß╗ŗ nhŲ░ sau
Gi├Ī trß╗ŗ cß╗▒c ─æß║Īi cß╗¦a h├Ām sß╗æ l├Ā:
A. x=2
B. y=-4
C. x=0
D. y=0
C├óu 5: Cho h├Ām sß╗æ \(y=f\left( x \right)\) x├Īc ─æß╗ŗnh tr├¬n \(\mathbb{R}\) c├│ ─æß║Īo h├Ām \(f'\left( x \right)=x\left( x-2 \right){{\left( x+1 \right)}^{2}}\left( {{x}^{2}}-4 \right)\). H├Ām sß╗æ ─æ├Ż cho c├│ bao nhi├¬u ─æiß╗ām cß╗▒c trß╗ŗ
A. 3.
B. 4
C. 2
D. 1
C├óu 6: Tiß╗ćm cß║Łn ngang cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=1+\frac{1}{x-1}\) l├Ā ─æŲ░ß╗Øng thß║│ng:
A. x=1
B. y=-1
C. y=1
D. y=0
C├óu 7: ─ÉŲ░ß╗Øng cong ß╗¤ h├¼nh dŲ░ß╗øi ─æ├óy l├Ā ─æß╗ō thß╗ŗ cß╗¦a mß╗Öt trong bß╗æn h├Ām sß╗æ dŲ░ß╗øi ─æ├óy. H├Ām sß╗æ ─æ├│ l├Ā h├Ām sß╗æ n├Āo ?
A. \(y=\frac{1}{9}{{x}^{3}}+\frac{1}{3}x+1.\)
B. \(y=\frac{1}{9}{{x}^{3}}-\frac{1}{3}x+1.\)
C. \(y=\frac{1}{4}{{x}^{4}}+{{x}^{2}}+1.\)
D. \(y=-{{x}^{3}}+{{x}^{2}}-x+1.\)
C├óu 8: ─Éß╗ō thß╗ŗ h├Ām sß╗æ \(y=-\frac{{{x}^{4}}}{2}+{{x}^{2}}+\frac{3}{2}\) cß║»t trß╗źc ho├Ānh tß║Īi mß║źy ─æiß╗ām?
A. 4
B. 3
C. 2
D. 0
C├óu 9: Vß╗øi a l├Ā sß╗æ thß╗▒c dŲ░ŲĪng t├╣y ├Į, \({{\log }_{5}}\left( 125a \right)\) bß║▒ng
A. \(3-{{\log }_{5}}a\).
B. \(3+{{\log }_{5}}a\).
C. \({{\left( {{\log }_{5}}a \right)}^{3}}\).
D. \(2+{{\log }_{5}}a\).
C├óu 10: ─Éß║Īo h├Ām cß╗¦a h├Ām sß╗æ \(y={{e}^{1-2x}}\) l├Ā:
A. \(y'=2{{e}^{1-2x}}\).
B. \(y'=-2{{e}^{1-2x}}\).
C. \(y'=-\frac{{{e}^{1-2x}}}{2}\).
D. \(y'={{e}^{1-2x}}\).
---(─Éß╗ā xem tiß║┐p nß╗Öi dung tß╗½ c├óu 11 ─æß║┐n c├óu 50 cß╗¦a ─æß╗ü thi sß╗æ 5 c├Īc em vui l├▓ng xem Online hoß║Ęc ─É─āng nhß║Łp v├Āo HOC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n tr├Łch dß║½n nß╗Öi dung Bß╗Ö 5 ─æß╗ü thi thß╗Ł THPT QG m├┤n To├Īn n─ām 2021-2022 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THPT Nguyß╗ģn Huß╗ć. ─Éß╗ā xem to├Ān bß╗Ö nß╗Öi dung c├Īc em ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
Ngo├Āi ra c├Īc em c├│ thß╗ā tham khß║Żo th├¬m mß╗Öt sß╗æ tŲ░ liß╗ću c├╣ng chuy├¬n mß╗źc sau ─æ├óy:
- Bß╗Ö 5 ─æß╗ü thi thß╗Ł THPT QG m├┤n To├Īn n─ām 2021-2022 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THPT L├Į Tß╗▒ Trß╗Źng
- Bß╗Ö 5 ─æß╗ü thi thß╗Ł THPT QG m├┤n To├Īn n─ām 2021-2022 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THPT Cao Thß║»ng
Ch├║c c├Īc em hß╗Źc tß╗æt!


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)