HOC247 xin gửi đến các em Tài liệu Đề thi giữa HK1 Toán 12 có đáp án năm 2023 – 2024 của Trường THPT Bùi Thị Xuân dưới đây. Tài liệu được tổng hợp với đáp án đi kèm nhằm giúp các em học sinh lớp 12 tiếp cận đề thi đồng thời ôn tập kiến thức cho kì thi giữa HK1 sắp tới và dễ dàng kiểm tra lại kết quả làm bài. Hy vọng tài liệu sẽ bổ ích với các em! Chúc các em làm bài thi thật tốt và đạt kết quả cao.
|
Sở giáo dục & đào tạo TPHCM THPT Bùi Thị Xuân
|
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 12 NĂM HỌC 2023-2024 Thời gian: 60p |
1. Đề thi
Câu 1. Cho khối chóp có diện tích đáy \(B=3\) và chiều cao \(h=2\). Thể tích khối chóp đã cho bằng
A. 6 B. 12 C. 2 D. 3
Câu 2. Cho khối hộp hình chữ nhật có ba kích thước 2; 4; 6. Thể tích của khối hộp đã cho bằng
A. 16 B. 12 C. 48 D. 8
Câu 3. Cho khối chóp S.ABC có SA vuông góc với đáy, \(SA=4,\text{ }AB=6,\text{ }BC=10\) và \(CA=8\). Tính thể tích V của khối chóp S.ABC.
A. \(V=40\) B. \(V=192\) C. \(V=32\). D. \(V=24\)
Câu 4. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?
A. 4 mặt phẳng B. 1 mặt phẳng C. 2 mặt phẳng D. 3 mặt phẳng
Câu 5. Cho hàm số \(y=(x-2)({{x}^{2}}+1)\) có đồ thị (C). Mệnh đề nào dưới đây đúng ?
A. \((C)\) cắt trục hoành tại hai điểm B. \((C)\) cắt trục hoành tại một điểm.
C. \((C)\) không cắt trục hoành. D. \((C)\) cắt trục hoành tại ba điểm.
Câu 6. Cho hàm số \(y=f(x)\) có đạo hàm \({f}'(x)={{x}^{2}}+1\), \(\forall x\in \mathbb{R}\). Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng \((-\infty ;0)\).
B. Hàm số nghịch biến trên khoảng \((1;+\infty )\).
C. Hàm số nghịch biến trên khoảng \((-1;1)\).
D. Hàm số đồng biến trên khoảng \((-\infty ;+\infty )\).
Câu 7. Cho hàm số \(y=f(x)\) có bảng biến thiên sau
.jpg?enablejsapi=1)
Mệnh đề nào dưới đây đúng ?
A. Hàm số có bốn điểm cực trị B. Hàm số không có cực đại.
C. Hàm số đạt cực tiểu tại \(x=2\). D. Hàm số đạt cực tiểu tại \(x=-5\).
Câu 8. Tìm giá trị nhỏ nhất m của hàm số \(y={{x}^{4}}-{{x}^{2}}+13\) trên đoạn \([-2;3]\)
A. \(m=\frac{51}{4}\). B. \(m=\frac{49}{4}\). C. \(m=13\) D. \(m=\frac{51}{2}\)
Câu 9. Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A. \(y=\frac{1}{{{x}^{2}}+1}\) B. \(y=\frac{1}{{{x}^{2}}+x+1}\)
C. \(y=\frac{1}{{{x}^{4}}+1}\) D. \(y=\frac{1}{\sqrt{x}}\)
Câu 10. Cho hàm số \(y={{x}^{4}}-2{{x}^{2}}\). Mệnh đề nào dưới đây là đúng?
A. Hàm số nghịch biến trên khoảng \((-\infty ;-2)\)
B. Hàm số đồng biến trên khoảng \((-\infty ;-2)\)
C. Hàm số đồng biến trên khoảng \((-1;1)\)
D. Hàm số nghịch biến trên khoảng \((-1;1)\)
Câu 11. Cho hàm số \(y=f(x)\) có bảng biến thiên như sau
.jpg)
Tìm giá trị cực đại yCĐ và giá trị cực tiểu yCT của hàm số đã cho.
A. yCĐ \(=3\) và yCT \(=-2\) B. yCĐ \(=3\) và yCT \(=0\).
C. yCĐ \(=-2\) và yCT \(=2\). D. yCĐ \(=2\) và yCT \(=0\).
Câu 12. Hàm số nào sau đây đồng biến trên khoảng \((-\infty ;+\infty )\)
A. \(y=\frac{x+1}{x+3}\). B. \(y={{x}^{3}}+x\).
C. \(y=\frac{x-1}{x-2}\) D. \(y=-{{x}^{3}}-3x\).
Câu 13. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
A. \(y={{x}^{4}}-2{{x}^{2}}+1\). B. \(y=-{{x}^{4}}+2{{x}^{2}}+1\).
C. \(y=-{{x}^{3}}+3{{x}^{2}}+1\). D. \(y={{x}^{3}}-3{{x}^{2}}+3\).
Câu 14. Cho hàm số \(y={{x}^{3}}-3{{x}^{2}}\). Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng \((0;2)\)
B. Hàm số nghịch biến trên khoảng \((2;+\infty )\)
C. Hàm số đồng biến trên khoảng \((0;2)\)
D. Hàm số nghịch biến trên khoảng \((-\infty ;0)\)
Câu 15. Đường cong hình bên là đồ thị của hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) với a, b, c là các ố thực. Mệnh đề nào dưới đây đúng ?
A. Phương trình \(y'=0\) có ba nghiệm thực phân biệt.
B. Phương trình \(y'=0\) có hai nghiệm thực phân biệt.
C. Phương trình \(y'=0\) vô nghiệm trên tập số thực.
D. Phương trình \(y'=0\) có đúng một nghiệm thực.
Câu 16. Tìm số tiệm cận của đồ thị hàm số \(y=\frac{{{x}^{2}}-5x+4}{{{x}^{2}}-1}\).
A. \(3\). B. \(2\) C. \(0\) D. \(1\).
Câu 17. Tìm giá trị lớn nhất M của hàm số \(y={{x}^{4}}-2{{x}^{2}}+3\) trên đoạn \([0;\sqrt{3}]\)
A. \(M=9\) B. \(M=8\sqrt{3}\) C. \(M=1\) D. \(M=6\)
Câu 18. Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) \(\left( a,\ b,\ c,\ d\in \mathbb{R} \right)\) có đồ thị như hình vẽ bên.
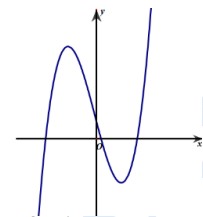
Số điểm cực trị của hàm số đã cho là
A. 2 B. 0 C. 3 D. 1
Câu 19. Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
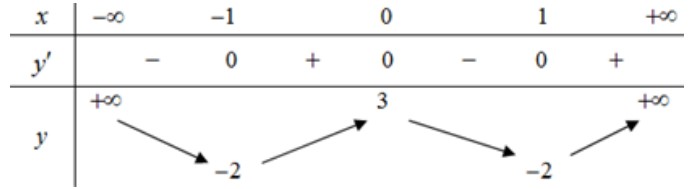
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. \(\left( 1;+\infty \right)\) B. \(\left( -\infty ;0 \right)\).
C. \(\left( 0;1 \right)\). D. \(\left( -1;0 \right)\).
Câu 20. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
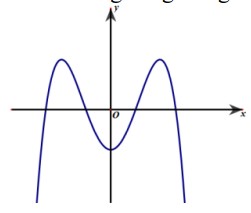
A. \(y={{x}^{4}}-3{{x}^{2}}-1\). B. \(y={{x}^{3}}-3{{x}^{2}}-1\).
C. \(y=-{{x}^{4}}+3{{x}^{2}}-1\). D \(y=-{{x}^{3}}+3{{x}^{2}}-1\).
Câu 21. Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) \(\left( a,\ b,\ c,\ d\in \mathbb{R} \right)\). Đồ thị hàm số \(y=f\left( x \right)\) như hình vẽ bên.
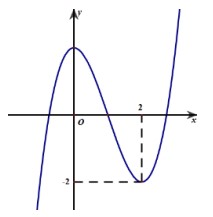
Số nghiệm thực của phương trình \(3f\left( x \right)+4=0\) là
A. 1 B. 0 C. 3 D. 2
Câu 22. Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+9}-3}{{{x}^{2}}+x}\) là
A. 1 B. 0 C. 3 D. 2
Câu 23. Cho khối chóp có đáy là hình vuông cạnh a, chiều cao bằng 2a. Thể tích của khối chóp đã cho bằng
A. \(4{{a}^{3}}\). B. \(2{{a}^{3}}\). C. \(\frac{2}{3}{{a}^{3}}\). D. \(\frac{4}{3}{{a}^{3}}\).
Câu 24. Cho khối lăng trụ đứng \(ABC.A'B'C'\) có \(BB'=a\), đáy ABC là tam giác vuông cân tại B và \(AC=a\sqrt{2}\). Tính thể tích V của khối lăng trụ đã cho.
A. \(V={{a}^{3}}\). B. \(V=\frac{{{a}^{3}}}{3}\). C. \(V=\frac{{{a}^{3}}}{6}\). D. \(V=\frac{{{a}^{3}}}{2}\).
Câu 25. Mặt phẳng \((A{B}'{C}')\) chia khối lăng trụ \(ABC.A'B'C'\) thành các khối đa diện nào ?
A. Một khối chóp tam giác và một khối chóp ngũ giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tam giác.
D. Hai khối chóp tứ giác.
---(Để xem tiếp nội dung đề thi các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
2. Đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
C |
C |
A |
B |
D |
C |
A |
D |
A |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
B |
B |
D |
A |
A |
B |
D |
A |
C |
C |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
C |
D |
C |
D |
B |
A |
B |
A |
C |
B |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
D |
A |
C |
C |
C |
B |
B |
B |
A |
B |
|
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
C |
A |
C |
D |
A |
D |
C |
D |
C |
D |
Trên đây là một phần trích đoạn nội dung Đề thi giữa HK1 môn Toán 12 năm 2023-2024 THPT Bùi Thị Xuân có đáp án. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Mời các em tham khảo tài liệu có liên quan:
Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.







