Bài tập 10 tr 101 sách BT Toán lớp 9 Tập 2
Cho tam giác \(ABC\) có \(AB > AC.\) Trên cạnh \(AB\) lấy một điểm \(D\) sao cho \(AD = AC.\) Vẽ đường tròn tâm \(O\) ngoại tiếp tam giác \(DBC.\) Từ \(O\) lần lượt hạ các đường thẳng vuông góc \(OH,\) \(OK\) xuống \(BC\) và \(BD\) (\(H \in BC,K \in BD\)).
\(a)\) Chứng minh rằng \(OH < OK.\)
\(b)\) So sánh hai cung nhỏ \(BD\) và \(BC.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một tam giác, độ dài một cạnh lớn hơn hiệu độ dài hai cạnh còn lại.
+) Trong một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
+) Với hai cung nhỏ trong một đường tròn, dây lớn hơn căng cung lớn hơn.
Lời giải chi tiết
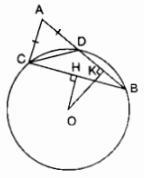
a) Trong ∆ABC ta có:
BC > AB – AC (bất đẳng thức tam giác)
Mà AC = AD (gt)
\( \Rightarrow \) BC > AB – AD
Hay BC > BD
Trong (O) ta có: BC > BD
\( \Rightarrow \) OH < OK (dây lớn hơn gần tâm hơn)
b) Ta có dây cung BC > BD
Suy ra: \(\overparen{BC}\) > \(\overparen{BD}\) (dây lớn hơn căng cung lớn hơn).
-- Mod Toán 9 HỌC247
-
Chứng minh SA^2 = SC.SB
bởi Nguyễn Trà Giang
13/02/2019
Cho (O) đường kính AB, trên tiếp tuyến tại A, lấy SB cắt (O) tại C. Chứng minh : SA2 = SC.SB
Theo dõi (0) 2 Trả lời -
Bài 11 trang 72 SGK Toán 9 tập 1
bởi het roi
21/02/2019
Bài 11 (SGK trang 72)Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O').
a) So sánh các cung nhỏ BC, BD.
b) Chứng minh rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau).
Theo dõi (0) 2 Trả lời
