Bài tập 2.2 tr 101 sách BT Toán lớp 9 Tập 2
Cho hình thoi \(ABCD.\) Vẽ đường tròn tâm \(A,\) bán kính \(AD.\) Vẽ đường tròn tâm \(C,\) bán kính \(CB.\) Lấy điểm \(E\) bất kỳ trên đường tròn tâm \(A\) (không trùng với \(B\) và \(D\)), điểm \(F\) trên đường tròn tâm \(C\) sao cho \(BF\) song song với \(DE.\) So sánh hai cung nhỏ \(DE\) và \(BF.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong hình thoi, hai đường chéo là các đường phân giác của các góc của hình thoi.
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải chi tiết
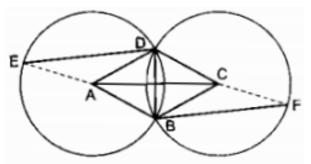
Ta có \((A; AD)\) và \((C; CB)\) có bán kính \(AD = CB\) là cạnh của hình thoi \(ABCD\) nên hai đường tròn đó bằng nhau.
Vì \(AD = AB = CD = CB\)
Suy ra \((A; AD)\) và \((C; CB)\) cắt nhau tại \(B\) và \(D.\)
\(DE // BF\;\; (gt)\)
\( \Rightarrow \widehat {EDB} = \widehat {FBD} \) (so le trong)
\(\Rightarrow \widehat {EDA} + \widehat {ADB} = \widehat {FBC} + \widehat {CBD}\)
Mà \(\widehat {ADB} = \widehat {CBD}\) (tính chất hình thoi)
Suy ra: \(\widehat {EDA} = \widehat {FBC}\) \((1)\)
\(∆ADE\) cân tại \(A\) \( \Rightarrow \widehat {EAD} = {180^0} - 2\widehat {EDA}\) \( (2)\)
\(∆CBF\) cân tại \(C\) \( \Rightarrow \widehat {BCF} = {180^0} - 2\widehat {FBC}\) \( (3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat {EAD} = \widehat {BCF}\)
\( sđ \overparen{DE}= \widehat {EAD}\)
\(sđ \overparen{BF}= \widehat {BCF}\)
Vì \((A; AD)\) và \((C; CB)\) bằng nhau nên \(\overparen{DE}= \overparen{BF}\)
-- Mod Toán 9 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





