HOC247 xin gß╗Łi ─æß║┐n c├Īc em hß╗Źc sinh mß╗Öt b├Āi giß║Żng ─æß║┐n tß╗½ s├Īch To├Īn 8 Kß║┐t nß╗æi tri thß╗®c vß╗øi nß╗Öi dung Ba trŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng cß╗¦a hai tam gi├Īc. B├Āi n├Āy cung cß║źp cho c├Īc em ba trŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng cß╗¦a tam gi├Īc ─æß╗ōng thß╗Øi c├│ thß╗ā ├Īp dß╗źng v├Āo c├Īc b├Āi tß║Łp thß╗▒c tiß╗ģn. Hy vß╗Źng rß║▒ng th├┤ng qua b├Āi giß║Żng n├Āy, c├Īc em sß║Į c├│ kß║┐t quß║Ż hß╗Źc tß║Łp tß╗æt v├Ā ─æß║Īt ─æŲ░ß╗Żc th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
T├│m tß║»t l├Į thuyß║┐t
1.1. TrŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng thß╗® nhß║źt cß╗¦a tam gi├Īc
|
TrŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng cß║Īnh ŌĆō cß║Īnh ŌĆō cß║Īnh Nß║┐u ba cß║Īnh cß╗¦a tam gi├Īc n├Āy tß╗ē lß╗ć vß╗øi ba cß║Īnh cß╗¦a tam gi├Īc kia th├¼ hai tam gi├Īc ─æ├│ ─æß╗ōng dß║Īng vß╗øi nhau. |

\(\left\{ \begin{array}{l}\Delta ABC,\Delta A'B'C';\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\end{array} \right. \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
1.2. TrŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng thß╗® hai cß╗¦a tam gi├Īc
|
TrŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng cß║Īnh ŌĆō g├│c ŌĆō cß║Īnh Nß║┐u hai cß║Īnh cß╗¦a tam gi├Īc n├Āy tß╗ē lß╗ć vß╗øi hai cß║Īnh cß╗¦a tam gi├Īc kia v├Ā hai g├│c tß║Īo bß╗¤i c├Īc cß║Ęp cß║Īnh ─æ├│ bß║▒ng nhau th├¼ hai tam gi├Īc ─æ├│ ─æß╗ōng dß║Īng vß╗øi nhau. |
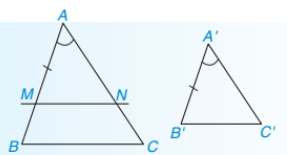
\(\left\{ \begin{array}{l}\Delta ABC,\Delta A'B'C';\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}},\widehat {A'} = \widehat A\end{array} \right. \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
Nhß║Łn x├®t: Nß║┐u \(\Delta A'B'C' \backsim \Delta ABC\) theo tß╗ē sß╗æ k v├Ā AM, AŌĆÖMŌĆÖ lß║¦n lŲ░ß╗Żt l├Ā c├Īc ─æŲ░ß╗Øng trung tuyß║┐n cß╗¦a \(\Delta ABC\) v├Ā \(\Delta A'B'C'\) th├¼ \(\frac{{A'M'}}{{AM}} = k\).
1.3. TrŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng thß╗® ba cß╗¦a tam gi├Īc
|
TrŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng g├│c ŌĆō g├│c Nß║┐u hai g├│c cß╗¦a tam gi├Īc n├Āy lß║¦n lŲ░ß╗Żt bß║▒ng hai g├│c cß╗¦a tam gi├Īc kia th├¼ hai tam gi├Īc ─æ├│ ─æß╗ōng dß║Īng vß╗øi nhau. |
.png)
\(\left\{ \begin{array}{l}\Delta ABC,\Delta A'B'C';\\\widehat {A'} = \widehat A,\widehat {B'} = \widehat B\end{array} \right. \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
Nhß║Łn x├®t: \(\Delta A'B'C' \backsim \Delta ABC\) theo tß╗ē sß╗æ k v├Ā AM, AŌĆÖMŌĆÖ lß║¦n lŲ░ß╗Żt l├Ā c├Īc ─æŲ░ß╗Øng ph├ón gi├Īc cß╗¦a \(\Delta ABC\) v├Ā \(\Delta A'B'C'\) th├¼ \(\frac{{A'M'}}{{AM}} = k\).
B├Āi tß║Łp minh hß╗Źa
B├Āi 1: Cho g├│c BAC v├Ā c├Īc ─æiß╗ām M, N lß║¦n lŲ░ß╗Żt tr├¬n c├Īc ─æoß║Īn thß║│ng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\).
a) Chß╗®ng minh rß║▒ng ╬öABN ~ ╬öACM.
b) Gß╗Źi I l├Ā giao ─æiß╗ām cß╗¦a BN v├Ā CM. CMR: \(IB.IN=IC.IM\).
HŲ░ß╗øng dß║½n giß║Żi:
a) X├®t tam gi├Īc ABN v├Ā tam gi├Īc ACM
Ta c├│ g├│c A chung v├Ā \(\widehat{ABN}=\widehat{ACM}\).
=> ΔABN ~ ΔACM.
b) Ta có ΔABN ~ ΔACM
Suy ra \(\widehat{ANB}=\widehat{AMC}\).
M├Ā \(\widehat{ANB}+\widehat{CNB}=180┬░\).
nên \(\widehat{AMC}+\widehat{BMC}=180°\).
=> \(\widehat{CNB}=\widehat{BMC}\).
X├®t tam gi├Īc IBM v├Ā tam gi├Īc ICN c├│
\(\widehat{CNB}=\widehat{BMC}\) v├Ā \(\widehat{IBM}=\widehat{ICN}\).
=> ΔIBM ~ ΔICN (g.g)
=> \(\frac{IB}{IC}=\frac{IM}{IN}\).
=> \(IB.IN=IC.IM\).
B├Āi 2: Cho tam gi├Īc ABC c├│ \(AB=12cm, AC=5cm\). Tr├¬n c├Īc tia AB, AC lß║¦n lŲ░ß╗Żt lß║źy c├Īc ─æiß╗ām M, N sao cho \(AM=10cm, AN=8cm\). Chß╗®ng minh rß║▒ng \(\Delta ABC\) ~ \(\Delta ANM\).
HŲ░ß╗øng dß║½n giß║Żi
Ta c├│:
\(AB=12cm , AN=8cm => \frac{AN}{AB}=\frac{8}{12}=\frac{2}{3}\).
\(AC=5cm, AM=10cm => \frac{AM}{AC}=\frac{10}{15}=\frac{2}{3}=> \frac{AN}{AB}=\frac{AM}{AC}\).
X├®t hai tam gi├Īc ABC v├Ā tam gi├Īc ANM, c├│:
\(\frac{AN}{AB}=\frac{AM}{AC}\) v├Ā g├│c A chung.
=> ΔABC ~ ΔANM' (c.g.c)
3. Luyß╗ćn tß║Łp B├Āi 34 To├Īn 8 Tß║Łp 2 - Kß║┐t nß╗æi tri thß╗®c
Qua b├Āi hß╗Źc n├Āy, c├Īc em sß║Į ho├Ān th├Ānh mß╗Öt sß╗æ mß╗źc ti├¬u m├Ā b├Āi ─æŲ░a ra nhŲ░ sau:
- Ba trŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng cß╗¦a hai tam gi├Īc.
- ├üp dß╗źng c├Īc trŲ░ß╗Øng hß╗Żp ─æß╗ōng dß║Īng cß╗¦a hai tam gi├Īc v├Āo c├Īc vß║źn ─æß╗ü thß╗▒c tiß╗ģn.
3.1. Trß║»c nghiß╗ćm B├Āi 34 To├Īn 8 Tß║Łp 2 - Kß║┐t nß╗æi tri thß╗®c
C├Īc em c├│ thß╗ā hß╗ć thß╗æng lß║Īi nß╗Öi dung kiß║┐n thß╗®c ─æ├Ż hß╗Źc ─æŲ░ß╗Żc th├┤ng qua b├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 8 Kß║┐t nß╗æi tri thß╗®c B├Āi 34 cß╗▒c hay c├│ ─æ├Īp ├Īn v├Ā lß╗Øi giß║Żi chi tiß║┐t.
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c v├Ā nß║»m vß╗»ng hŲĪn vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK B├Āi 34 To├Īn 8 Tß║Łp 2 - Kß║┐t nß╗æi tri thß╗®c
C├Īc em c├│ thß╗ā xem th├¬m phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 8 Kß║┐t nß╗æi tri thß╗®c B├Āi 34 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Hoß║Īt ─æß╗Öng 1 trang 83 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
C├óu hß╗Åi trang 84 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
Luyß╗ćn tß║Łp 1 trang 85 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
Hoß║Īt ─æß╗Öng 2 trang 85 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
C├óu hß╗Åi trang 86 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
Luyß╗ćn tß║Łp 2 trang 87 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
Tranh luß║Łn trang 87 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
Hoß║Īt ─æß╗Öng 3 trang 88 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
Hoß║Īt ─æß╗Öng 4 trang 88 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
C├óu hß╗Åi trang 89 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
Luyß╗ćn tß║Łp 3 trang 89 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
B├Āi 9.5 trang 90 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
B├Āi 9.6 trang 90 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
B├Āi 9.7 trang 90 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
B├Āi 9.8 trang 90 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
B├Āi 9.9 trang 90 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
B├Āi 9.10 trang 90 SGK Toa╠ün 8 Kß║┐t nß╗æi tri thß╗®c T├ó╠Żp 2 - KNTT
B├Āi t├ó╠Żp 9.12 trang 55 SBT To├Īn 8 Tß║Łp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
B├Āi t├ó╠Żp 9.13 trang 55 SBT To├Īn 8 Tß║Łp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
B├Āi t├ó╠Żp 9.14 trang 55 SBT To├Īn 8 Tß║Łp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
B├Āi t├ó╠Żp 9.15 trang 55 SBT To├Īn 8 Tß║Łp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
B├Āi t├ó╠Żp 9.16 trang 55 SBT To├Īn 8 Tß║Łp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
4. Hß╗Åi ─æ├Īp B├Āi 34 To├Īn 8 Tß║Łp 2 - Kß║┐t nß╗æi tri thß╗®c
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 8 Hß╗īC247











