Bài tập 9.16 trang 55 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT

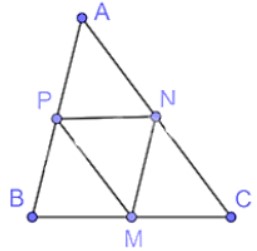
Tam giác ABC có:

M, N lần lượt là trung điểm của BC, CA

Nên MN là đường trung bình của tam giác ABC.

Do đó, MN // AB và $\frac{AB}{MN}=2$ .

Chứng minh tương tự ta có:$\frac{BC}{PN}=2$; $\frac{AC}{PM}=2$ .

Tam giác ABC và tam giác MNP có:

$\frac{AB}{MN}=\frac{BC}{PN}=\frac{AC}{PM}$(= 2).

Nên ∆ABC ᔕ ∆MNP (c.c.c) theo tỉ số đồng dạng là 2.

-- Mod Toán 8 HỌC247