Giải bài 1.24 trang 16 SBT Toán 7 Kết nối tri thức tập 1 - KNTT

Phương pháp giải:

-Tích của đường chéo: \({2^1}{.2^4}{.2^7} = {2^{12}}\)

-Do đó: tích các số trong mỗi hàng, mỗi cột, mỗi đường chéo bằng \({2^{12}}\)

Lời giải chi tiết:

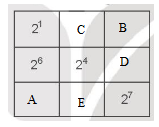
Ta cần tìm các số ở vị trí A,B,C,D,E.

Ta có: Tích của đường chéo chính: \({2^1}{.2^4}{.2^7} = {2^{12}}\)

Do đó: tích các số trong mỗi hàng, mỗi cột, mỗi đường chéo bằng \({2^{12}}\)

A: \({2^{12}}:\left( {{2^1}{{.2}^6}} \right) = {2^{12}}:{2^7}={2^{12 - 7}} = {2^5}\)

B:\({2^{12}}:\left( {{2^5}{{.2}^4}} \right) = {2^{12}}:{2^9} ={2^{12 - 9}}= {2^3}\)

C: \({2^{12}}:\left( {{2^1}{{.2}^3}} \right) = {2^{12}}:{2^4} = {2^{12 - 4}} = {2^8}\)

D:\({2^{12}}:\left( {{2^6}{{.2}^4}} \right) = {2^{12}}:{2^{10}} ={2^{12 - 10}}= {2^2}\)

E:\({2^{12}}:\left( {{2^5}{{.2}^7}} \right) = {2^{12}}:{2^{12}} ={2^{12 - 12}}= {2^0}\)

Từ đó ta có bảng sau:

-- Mod Toán 7 HỌC247