Giải bài tập Toán 7 Cánh diều Bài 7: Tam giác cân

Cầu Long Biên bắc qua sông Hồng ở Thủ đô Hà Nội gợi nên hình ảnh tam giác ABC có sự đối xứng và cân bằng.

Tam giác ABC như vậy gọi là tam giác gì?

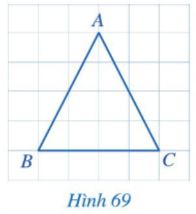
Trong Hình 68, hai cạnh AB và AC của tam giác ABC có bằng nhau hay không?

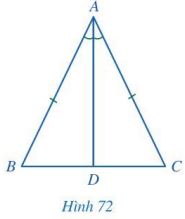
Cho tam giác ABC cân tại A, tia phân giác của góc A cắt cạnh BC tại D (Hình 72).

a) Hai tam giác ABD và ACD có bằng nhau hay không? Vì sao?

b) Hai góc B và C có bằng nhau hay không? Vì sao?

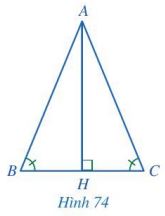
Cho tam giác ABC thỏa mãn \(\widehat B = \widehat C\). Kẻ AH vuông góc với BC, H thuộc BC (Hình 74).

a) Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?

b) Hai cạnh AB và AC có bằng nhau hay không? Vì sao?

Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC, cắt cạnh AC tại N. Chứng minh tam giác AMN cân.

Dùng thước thẳng (có chia đơn vị) và compa vẽ tam giác cân ABC có cạnh đáy BC = 4 cm, cạnh bên AB = AC = 3 cm.

Cho tam giác ABC cân tại A có M là trung điểm cạnh AC và N là trung điểm cạnh AB. Chứng minh \(BM = CN\)

Cho tam giác ABC có \(\widehat A = 120^\circ \). Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.

Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.

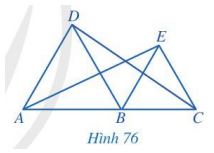
Trong Hình 76, cho biết các tam giác ABD và BCE là tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

a) AD // BE và BD // CE;

b) \(\widehat {ABE} = \widehat {DBC} = 120^\circ \);

c) AE = CD.

Trong thiết kế của một ngôi nhà, độ nghiêng của mái nhà so với phương nằm ngang phải phù hợp với kết cấu của ngôi nhà và vật liệu làm mái nhà. Hình 77 mô tả mặt cắt đứng của ngôi nhà, trong đó độ nghiêng của mái nhà so với phương nằm ngang được biểu diễn bởi số đo góc ở đáy của tam giác ABC cân tại A.

Tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong mỗi trường hợp sau:

a) Góc ở đỉnh A là (khoảng) 120° đối với mái nhà lợp bằng ngói;

b) Góc ở đỉnh A là (khoảng) 140° đối với mái nhà lợp bằng fibro xi măng;

c) Góc ở đỉnh A là (khoảng) 148° đối với mái nhà lợp bằng tôn.

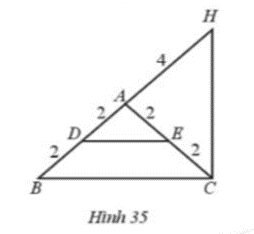
Tìm các tam giác cân trên Hình 35. Kể tên các cạnh bên, cạnh đáy, góc ở đáy, góc ở đỉnh của mỗi tam giác cân đó.

Ở Hình 36 có AB song song cới CD, BC song song với AD. Tia phân giác của góc BAD cắt BC tại E và cắt tia DC tại F.

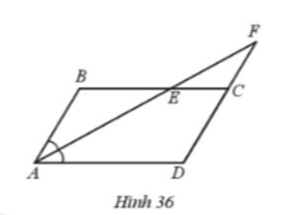
a) Chứng minh các tam giác ABE, CEF, DAF là các tam giác cân.

b) Tính số đo mỗi góc của tam giác ADF, biết \(\widehat {BAD} = 60^\circ \)

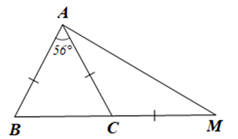
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 56^\circ \). Trên tia đối của tia CB lấy điểm M sao cho AC = CM. Tính số đo mỗi góc của tam giác ABM.

Cho tam giác ABC. Gọi I là trung điểm của BC. Tính số đo góc BAC, biết IA = IB = IC.

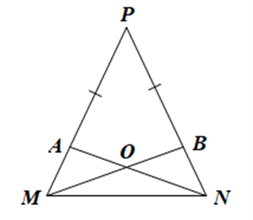
Cho tam giác MNP cân tại P. Lấy điểm A trên cạnh PM, điểm B trên cạnh PN sao cho PA = PB. Gọi O là giao điểm của NA và MB. Chứng minh tam giác OMN là tam giác cân.

Cho tam giác ABC cân tại A có \(\widehat {BAC} = 120^\circ \). Trên cạnh BC lấy các điểm D, E sao cho BD = BA, CE = CA.

a) Chứng minh các tam giác BAD, CAE, AED là các tam giác cân.

b) Tính số đo mỗi góc của tam giác ADE.

Cho Hình 37 có AB = AC = BC = BD = CE, \(\widehat {ABD} = \widehat {ACE} = 90^\circ \)

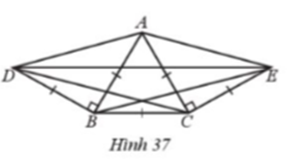
a) Chứng minh tam giác AED là tam giác cân.

b) Tính số đo các góc của tam giác ADE.

c) Chứng minh DC = BE

Cho tam giác đều ABC. Gọi E, D, F là ba điểm lần lượt nằm trên ba cạnh AB, AC, BC sao cho AD = CF = BE. Chứng minh tam giác DEF là tam giác đều. 

Cho tam giác ABC. Trên cạnh BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi O là giao điểm của DE và BC. Biết OD = OE. Chứng minh tam giác ABC là tam giác cân.