Giải bài 47 trang 83 SBT Toán 7 Cánh diều tập 2
Cho tam giác MNP cân tại P. Lấy điểm A trên cạnh PM, điểm B trên cạnh PN sao cho PA = PB. Gọi O là giao điểm của NA và MB. Chứng minh tam giác OMN là tam giác cân.
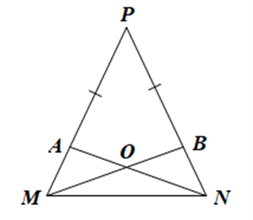
Hướng dẫn giải chi tiết Bài 47
Phương pháp giải
- Sử dụng tam giác MNP cân tại P chứng minh AM = BN.
- Chứng minh: \(\Delta AMN = \Delta BNM(c - g - c)\)
- Chứng minh: \(\widehat {ONM} = \widehat {OMN}\) suy ra tam giác ONM cân tại O.
Lời giải chi tiết
Vì ∆MNP cân tại P nên ta có:
PM = PN (hai cạnh bên), \(\widehat {PMN} = \widehat {PNM}\) (hai góc ở đáy).
Ta có PM = PA + AM, PN = PB + BN.
Mà PM = PN (chứng minh trên), PA = PB (giả thiết).
Suy ra AM = BN.
Xét ∆AMN và ∆BNM có:
AM = BN (chứng minh trên),
MN là cạnh chung,
\(\widehat {AMN} = \widehat {BNM}\) (do \(\widehat {PMN} = \widehat {PNM}\))
Do đó ∆AMN = ∆BNM (c.g.c).
Suy ra \(\widehat {ANM} = \widehat {BMN}\) (hai góc tương ứng).
Hay \(\widehat {ONM} = \widehat {OMN}\)
Do đó tam giác ONM cân tại O.
Vậy tam giác OMN là tam giác cân tại O.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





