Giải bài 62 tr 48 sách BT Toán lớp 7 Tập 2
Cho hình 12, \(M\) là một điểm tùy ý nằm trên đường thẳng \(a.\) Vẽ điểm \(C\) sao cho \(a\) là đường trung trực của \(AC.\)
a) Hãy so sánh \(MA + MB\) với \(BC.\)
b) Tìm vị trí của điểm \(M\) trên đường thẳng \(a\) để \(MA + MB\) là nhỏ nhất.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó
+) Trong một tam giác, tổng hai cạnh luôn lớn hơn cạnh còn lại
Lời giải chi tiết
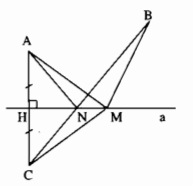
a) Gọi N là giao điểm của BC với đường thẳng a.
Nếu M # N
Nối MC
a là đường trung trực của AC
M ∈ a
\( \Rightarrow \) MA = MC (tính chất đường trung trực) (1)
Trong ∆MBC ta có:
BC < MB + MC (bất đẳng thức tam giác) (2)
Thay (1) vào (2) ta có: BC < MA + MB
Nếu M trùng với N, ta nối NA
NA = NC (tính chất đường trung trực)
MA + MB = NA + NB = NC + NB = BC
Vậy: MA + MB ≥ BC
b) Theo chứng minh A ta có: Khi M trùng với N.
MA + MB = BC là bé nhất
Vậy M là giao điểm của BC với đường thẳng a thì MA + MB bé nhất.
-- Mod Toán 7 HỌC247
-
Xđ dạng của tam giác có giao điểm phân giác trùng với giao điểm các đường trung trực
bởi thu thủy
28/03/2018
Ai giúp em bài này với ạ
Xác định dạng của tam giác có giao điểm các phân giác trùng với giao điểm các đường trung trực.
Theo dõi (0) 2 Trả lời -
Tam giác ABC có A là góc tù, đtròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ
bởi ngọc trang
28/03/2018
Ai đó giúp em với
Tam giác ABC có \(\widehat A \) là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở P và E. Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ.
Theo dõi (0) 2 Trả lời -
Trên đường trung trực d của đt AB lấy điểm M và E, F là giao điểm của AP, BP với MB, MA
bởi thanh hằng
28/03/2018
ai giải hộ e bài này vs ạ
Trên đường trung trực d của đoạn thẳng AB lấy điểm M. Hạ \(MH \bot AB\). Trên đoạn MH lấy điểm P. Gọi E là giao điểm của AP với MB. Gọi F là giao điểm của BP với MA.
a. Chứng minh MH là phân giác góc AMB.
b. Chứng minh MH là trung trực của đoạn EF
c. Chứng minh AF = BE.
Theo dõi (0) 2 Trả lời -
Cho hai đoạn thẳng phân biệt AB và CD, O là giao điếm hai đường TT của AB và CD
bởi thanh duy
29/03/2018
Giúp em nhanh với mấy anh chị ơi
Cho hai đoạn thẳng phân biệt AB và CD. Gọi O là giao điếm hai đường trung trực của AB và CD. Có nhận xét gì về hai đoạn AB và CD. Nếu AB // CD thì có nhận xét gì về hai đường trung trực đó?
Theo dõi (0) 2 Trả lời -
Tam giác ABC, phân giác AD, trên AC lấy điểm E sao cho AE = AB, cmr AD vuông góc với BE
bởi khanh nguyen
29/03/2018
giải hộ e bài này vs ạ
Tam giác ABC có AC > AB, phân giác AD. Trên AC lấy điểm E sao cho AE = AB. Chứng minh rằng AD vuông góc với BE.
Theo dõi (0) 2 Trả lời -
Cho đoạn thẳng AB thuộc nửa mp bờ d, xđ điểm M thuộc d sao cho M cách đều hai điểm A, B
bởi minh vương
28/03/2018
Khó quá, mọi người giúp vs
Cho đoạn thẳng AB thuộc nửa mặt phảng bờ d. Xác định điểm M thuộc d sao cho điểm M cách đều hai điểm A, B.
Theo dõi (0) 2 Trả lời -
Cho m là đường TT của đoạn thẳng AB, C là điểm thuộc m, cmr Cn vuông góc với m
bởi hành thư
28/03/2018
giải hộ e bài này vs ạ
Cho m là đường trung trực của đoạn thẳng AB, C là điểm thuộc m. Gọi Cx là tia đối của tia CA, Cn là tia phân giác của góc BCx. Chứng minh rằng Cn vuông góc với m.
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC, tìm một điểm cách đều hai cạnh AB, AC và cách đều hai đỉnh A, B
bởi thanh hằng
28/03/2018
Ai giúp em bài này với ạ
Cho tam giác ABC. Hãy tìm một điểm cách đều hai cạnh AB, AC và cách đều hai đỉnh A, B.
Theo dõi (0) 2 Trả lời -
Bài toán về tam giác
bởi Manhtan Nguyen
19/01/2018
Cho tam giác ABC vuông tại A có AB=1/2 AC, AD là tia phân giác của góc BAC (D thuộc BC) E là trung điểm của AC
a) Chứng minh DE=DB
b) AB cắt ED tại K. Chứng minh tam giác DCK cân và B là trung điểm của AK
c) AD cắt CK tại H. Chứng minh AH vuông góc với CK
d) Biết AB=4 tính DK
Theo dõi (0) 1 Trả lời -
bài 1 Cho tam giác ABC vuông tại A, AB=AC, diểm D thuộc AB. Đường thẳng qua B vuông góc CD cắt đường thẳng CA ở K . C/m AK=BC
Theo dõi (0) 0 Trả lời -
hinh hoc lop 7
bởi Tran Hoang Minh
03/01/2018
Cho goc XOY co so do bang 120 do, diem A thuoc tia phan giac cau goc do ke AB vuong goc voi OX( Bthuoc Ox) e AC vuong goc voi OY(Cthuoc Oy).Tam giac ABC la tam giac gi? Vi sao?
Theo dõi (0) 1 Trả lời -
hinh hoc lop 7
bởi Tran Hoang Minh
03/01/2018
Cho tam giac ABC can tai A.Lay diem D thuoc canh AC, diem E thuoc canh AB sao cho AB sao cho AD=AE. a, so sanh goc ABD va goc ACE b, goi I la giao diem cua BD va CE.tam giac IBC la tam giac gi. Vi sao
Theo dõi (0) 1 Trả lời -
hinh hoc lop 7
bởi Tran Hoang Minh
03/01/2018
hai thanh AB va AC cua vi keo mot mai nha thuong bang nhau va thuong tao voi nhau 1 goc bang.a,145 do neu mai nha la ton . b,100 do neu mai nha la ngoi . Tinh goc ABC trong tung trong hop
Theo dõi (0) 1 Trả lời -
tổng ba cạnh của tam giác
bởi nguyễn công quyền
30/12/2017
cho đoạn thẳng BC gọi I là trung điểm của BC . Trên đường trung trực của BC lấy điểm A ( A khác I)
a , C/M tam giác AIB= tam giác AIC
b, C/M : AI là tia phân giác góc BAC
c, kẻ IH vuông góc AB , IK vuông gó AC. C/M IH =IK
GIÚP MÌNH VỚI CHUYỀN ĐI HỌC RỒI
Theo dõi (1) 2 Trả lời -
hinh hoc lop 7
bởi Tran Hoang Minh
12/12/2017
cho tam giac ABC co goc AH vuong voi goc BC tai H. Tren tia AH keo dai lay diem D sao cho HA=HD.
Chung minh rang
a, tam giac ABH=tam giac DBH b, chung minh CB la tia phan giac cua ACD
Theo dõi (0) 2 Trả lời
