Luyện tập 5 trang 92 SGK Toán 11 Cánh diều Tập 1 - CD

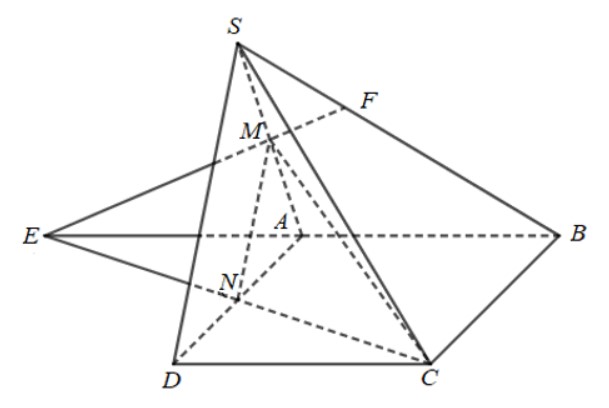
a)

+) Trong mặt phẳng \((ABCD)\): Gọi giao điểm của AB với NC là E.

Mà \(NC\) ⊂ \((CMN)\)

Suy ra: \((CMN)\) ∩ \(AB = {E}\).

+) Trong mặt phẳng \((SAB)\): Kéo dài EM cắt AB tại F.

Mà \(EM\) ⊂ \((CMN)\)

Suy ra \((SAB)\) ∩ \(EM = {F}\).

b)

+) Ta có: \(M\) ∈ \(SA\) mà \(SA\) ⊂ \((SAB)\) nên \(M\) ∈ \((SAB)\);

              \(M\) ∈ \(CM\) mà \(CM\) ⊂ \((CMN)\) nên \(M\) ∈ \((CMN)\).

Do đó M là giao điểm của hai mặt phẳng \((SAB)\) và \((CMN)\).

Ta lại có: \(AB\) ∩ \(CN = {E}\);

               \(AB\) ⊂ \((SAB)\);

               \(CN\) ⊂ \((CMN)\).

Do đó E là giao điểm của hai mặt phẳng \((SAB)\) và \((CMN)\).

Vì vậy \((SAB)\) ∩ \((CMN) = EM\).

+) Ta có: \(C\) ∈ \(SC\) mà \(SC\) ⊂ \((SBC)\);

               \(C\) ∈ \(CM\) mà \(CM\) ⊂ \((CMN)\).

Do đó C là giao điểm của hai mặt phẳng \((SBC)\) và \((CMN)\).

Ta lại có: \(SB\) ∩ \(EM = {F}\);

              \(SB\) ⊂ \((SBC)\);

              \(EM\) ⊂ \((CMN)\).

Do đó F là giao điểm của hai mặt phẳng \((SBC)\) và \((CMN)\).

Vì vậy \((SBC)\) ∩ \((CMN) = CF\).

-- Mod Toán 11 HỌC247