Bài tập 6 trang 95 SBT Toán 11 Tập 1 Cánh diều
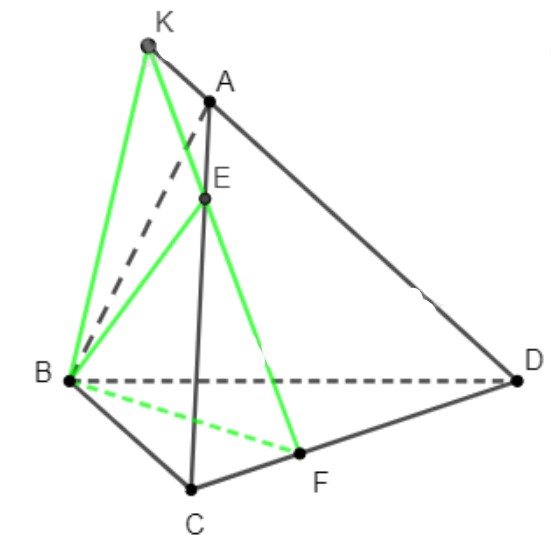
Cho tứ diện \(ABCD\). Trên các cạnh \(AC,{\rm{ }}CD\) lần lượt lấy các điểm \(E,{\rm{ }}F\) sao cho \(CE = 3EA,{\rm{ }}DF = 2FC\).
a) Xác định giao tuyến của mặt phẳng \(\left( {BEF} \right)\) với các mặt phẳng \(\left( {ABC} \right)\), \(\left( {ACD} \right)\), \(\left( {BCD} \right)\).
b) Xác định giao điểm \(K\) của đường thẳng \(AD\) với mặt phẳng \(\left( {BEF} \right)\).
c) Xác định giao tuyến của hai mặt phẳng \(\left( {BEF} \right)\) và \(\left( {ABD} \right)\).
Hướng dẫn giải chi tiết Bài tập 6
a) Giao tuyến của \(\left( {BEF} \right)\) và \(\left( {ABC} \right)\):
Ta có: \(B \in \left( {BEF} \right) \cap \left( {ABC} \right)\).
Mặt khác, ta có \(\left\{ \begin{array}{l}E \in \left( {BEF} \right)\\E \in AC \subset \left( {ABC} \right)\end{array} \right.\)
\(\Rightarrow E \in \left( {BEF} \right) \cap \left( {ABC} \right)\).
Như vậy giao tuyến của \(\left( {BEF} \right)\) và \(\left( {ABC} \right)\) là đường thẳng \(BE\).
Giao tuyến của \(\left( {BEF} \right)\) và \(\left( {ACD} \right)\):
Ta có: \(\left\{ \begin{array}{l}F \in \left( {BEF} \right)\\F \in CD \subset \left( {ACD} \right)\end{array} \right.\)
\(\Rightarrow F \in \left( {BEF} \right) \cap \left( {ACD} \right)\).
Mặt khác, \(\left\{ \begin{array}{l}E \in \left( {BEF} \right)\\E \in AC \subset \left( {ACD} \right)\end{array} \right.\)
\(\Rightarrow E \in \left( {BEF} \right) \cap \left( {ACD} \right)\).
Như vậy giao tuyển của \(\left( {BEF} \right)\) và \(\left( {ACD} \right)\) là đường thẳng \(EF\).
Giao tuyến của \(\left( {BEF} \right)\) và \(\left( {BCD} \right)\):
Ta có: \(B \in \left( {BEF} \right) \cap \left( {BCD} \right)\).
Mặt khác, \(\left\{ \begin{array}{l}F \in \left( {BEF} \right)\\F \in CD \subset \left( {BCD} \right)\end{array} \right.\)
\(\Rightarrow F \in \left( {BEF} \right) \cap \left( {BCD} \right)\)
Như vậy giao tuyển của \(\left( {BEF} \right)\) và \(\left( {BCD} \right)\) là đường thẳng \(BF\).
b) Trên mặt phẳng \(\left( {ACD} \right)\), lấy \(K\) là giao điểm của \(AD\) và \(EF\).
Ta có: \(\left\{ K \right\} = AD \cap EF\), mà \(EF \subset \left( {BEF} \right)\).
Suy ra \(\left\{ K \right\} = AD \cap \left( {BEF} \right)\), tức \(K\) là giao điểm của \(AD\) và \(\left( {BEF} \right)\).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 4 trang 94 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 5 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 7 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 8 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 9 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD





