Bài tập 5 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD

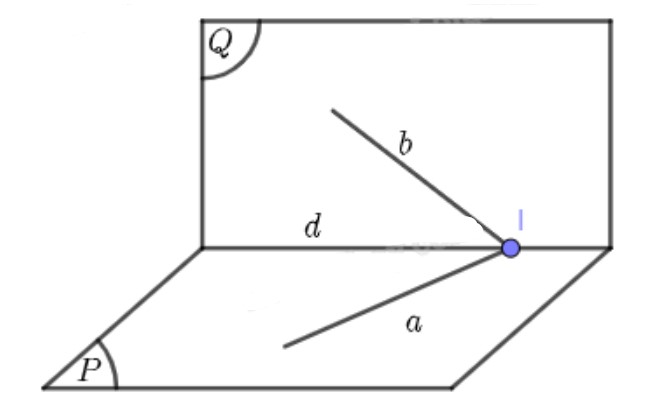
Gọi \(I\) là giao điểm của hai đường thẳng \(a\) và \(b\). Suy ra \(\left\{ \begin{array}{l}I \in a\\I \in b\end{array} \right.\)

Vì \(a \subset \left( P \right)\) và \(b \subset \left( Q \right)\).

Ta suy ra \(\left\{ \begin{array}{l}I \in \left( P \right)\\I \in \left( Q \right)\end{array} \right.\).

Tức là \(I\) thuộc giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).

Mà \(\left( P \right) \cap \left( Q \right) = d\), suy ra \(I \in d\).

Bài toán được chứng minh.

-- Mod Toán 11 HỌC247