Bài 6 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD

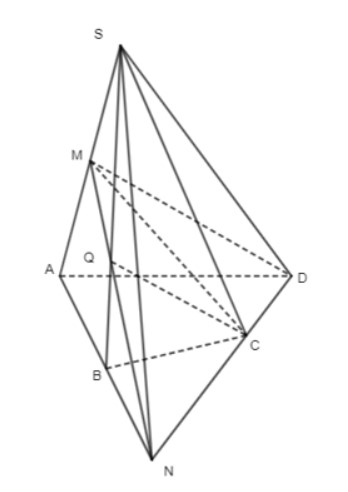
a) Trong mặt phẳng \((ABCD)\) ta có: gọi giao điểm của AB và CD là N.

Mà \(AB ⊂ (SAB)\)

Do đó \(CD ∩ (SAB) = {N}\).

b) Ta có: \(AB ∩ CD = {N}\);

              \(AB ⊂ (SAB)\);

               \(CD ⊂ (SCD)\)

Do đó N là giao điểm của \((SAB)\) và \((SCD)\).

Lại có: \(S ∈ (SAB)\) và \(S ∈ (SCD)\).

Nên S là giao điểm của \((SAB)\) và \((SCD)\).

Vì vậy \((SAB) ∩ (SCD) = SN\).

c) Ta có: \(C ∈ (SBC)\) và \(C ∈ (MCD)\).

Do đó C là giao điểm của \((SBC)\) và \((MCD)\).

Trong mặt phẳng \((SAB)\), gọi Q là giao điểm của MN và SB.

Mà \(MN ⊂ (MCD)\) và \(SB ⊂ (SBC)\)  

Suy ra Q là giao điểm của \((SBC)\) và \((MCD)\).

Vì vậy \((SBC) ∩ (MCD) = CQ\).

-- Mod Toán 11 HỌC247