Luyện tập 3 trang 103 SGK Toán 11 Cánh diều Tập 1
Ở Ví dụ 3, xác định giao tuyến của mặt phẳng \((R)\) với các mặt phẳng \((ABD),~(BCD),~(ACD)\)?
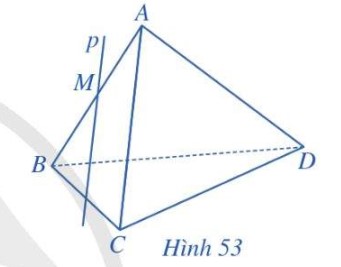
Hướng dẫn giải chi tiết Luyện tập 3

- Áp dụng định lí 2, ta có:
\((R)\) đi qua M và song song với BD, mà \(BD ⊂ (ABD)\) nên mặt phẳng \((R)\) cắt \((ABD)\) theo giao tuyến a đi qua M và song song với BD.
- Gọi N là giao điểm của p và BC.
Khi đó \(N ∈ (R)\).
Áp dụng định lí 2, ta có:
\((R)\) đi qua N và song song với BD, mà \(BD ⊂ (BCD)\) nên mặt phẳng \((R)\) cắt \((BCD)\) theo giao tuyến b đi qua N và song song với BD.
- Gọi P là giao điểm của a và AD, Q là giao điểm của b và CD.
Khi đó \(P ∈ (R)\) và \(P ∈ (ACD)\) nên P là giao điểm của \((R)\) và \((ACD)\);
\(Q ∈ (R)\) và \(Q ∈ (ACD)\) nên Q là giao điểm của \((R)\) và \((ACD)\).
Vậy \((R) ∩ (ACD) = PQ\).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 2 trang 102 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 3 trang 102 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 4 trang 103 SGK Toán 11 Cánh diều Tập 1 - CD
Luyện tập 4 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 1 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 2 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 3 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 4 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 5 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 6 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD
Bài tập 19 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 20 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 21 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 22 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 23 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 24 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 25 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD





