Bài tập 24 trang 104 SBT Toán 11 Tập 1 Cánh diều
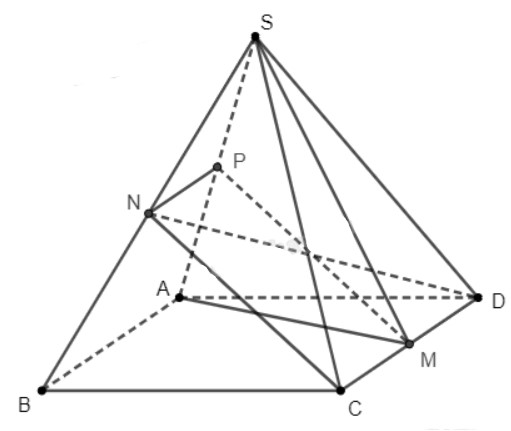
Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình bình hành. Gọi \(M\), \(N\) lần lượt là trung điểm của \(CD\), \(SB\).
a) Xác định giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {CDN} \right)\).
b) Chứng minh rằng đường thẳng \(CN\) song song với mặt phẳng \(\left( {SAM} \right)\).
Hướng dẫn giải chi tiết Bài tập 24
a) Vẽ \(NP\parallel AB\) với \(P \in SA\). Do \(AB\parallel CD\) nên ta suy ra \(NP\parallel CD\).
Ta có \(N \in \left( {SAB} \right) \cap \left( {CDN} \right)\).
Nên tồn tại giao tuyến (là đường thẳng đi qua \(N\)) của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {CDN} \right)\).
Mặt khác, ta có \(AB\parallel CD\), \(AB \subset \left( {SAB} \right)\), \(CD \subset \left( {CDN} \right)\).
Ta suy ra giao tuyến của \(\left( {SAB} \right)\) và \(\left( {CDN} \right)\) song song với \(CD\), tức là giao tuyến đó là đường thẳng \(NP\).
b) Do \(N\) là trung điểm của \(SB\), \(NP\parallel AB\) nên \(NP\) là đường trung bình của tam giác \(SAB\).
Suy ra \(NP = \frac{1}{2}AB\).
Mặt khác, do \(M\) là trung điểm của \(CD\) nên \(CM = \frac{1}{2}CD\).
Như vậy \(NP = CM\). Mặt khác, ta có \(NP\parallel CM\) nên tứ giác \(CMPN\) là hình bình hành.
Từ đó \(CN\parallel MP\). Do \(MP \subset \left( {SAM} \right)\) nên \(CN\parallel \left( {SAM} \right)\).
Bài toán dược chứng minh.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





