Bài tập 22 trang 104 SBT Toán 11 Tập 1 Cánh diều
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ACD\), điểm \(M\) nằm trên cạnh \(AB\) sao cho \(AM = 2MB\). Đường thẳng \(MG\) song song với mặt phẳng:
A. \(\left( {ACD} \right)\)
B. \(\left( {ABD} \right)\)
C. \(\left( {BCD} \right)\)
D. \(\left( {ABC} \right)\)
Hướng dẫn giải chi tiết Bài tập 22
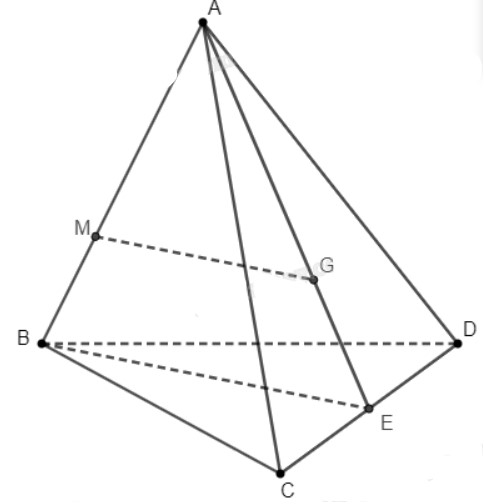
Do \(AM = 2MB \Rightarrow \frac{{AM}}{{AB}} = \frac{2}{3}\).
Gọi \(E\) là trung điểm của \(CD\). Do \(G\) là trọng tâm tam giác \(ACD\).
Ta suy ra ba điểm \(A\), \(G\), \(E\) thẳng hàng và \(\frac{{AG}}{{AE}} = \frac{2}{3}\).
Tam giác \(ABE\) có \(\frac{{AM}}{{AB}} = \frac{{AG}}{{AE}}\) nên theo định lí Thales đảo, \(GM\parallel BE\).
Mà \(BE \subset \left( {BCD} \right)\), ta suy ra \(GM\parallel \left( {BCD} \right)\).
Đáp án đúng là C.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 20 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 21 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 23 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 24 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 25 trang 104 SBT Toán 11 Tập 1 Cánh diều - CD





