Bài tập 26 trang 104 SBT Toán 11 Tập 1 Cánh diều
Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình bình hành. Gọi \(M\) là điểm chuyển động trên cạnh \(SC\) (\(M\) khác \(C\)), \(\left( P \right)\) là mặt phẳng chứa đường thẳng \(AM\) và song song với \(BD\). Chứng minh rằng mặt phẳng \(\left( P \right)\) luôn đi qua một đường thẳng cố định khi \(M\) chuyển động trên cạnh \(SC\)?
Hướng dẫn giải chi tiết Bài tập 26
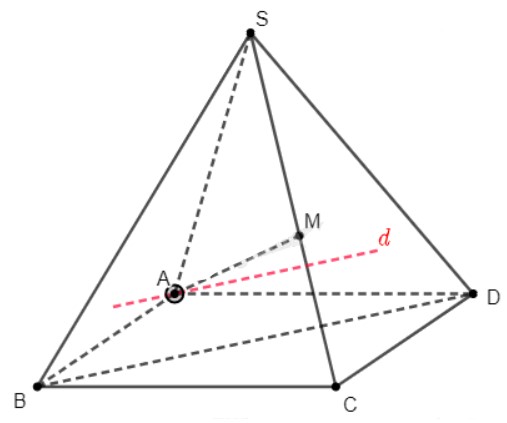
Trên mặt phẳng \(\left( {ABCD} \right)\), vẽ đường thẳng \(d\) đi qua \(A\) và song song với \(BD\).
Xét mặt phẳng \(\left( P \right)\) và \(\left( {ABCD} \right)\).
Ta có \(A \in AM \subset \left( P \right)\) và \(A \in \left( {ABCD} \right)\).
Nên giao tuyến của \(\left( P \right)\) và \(\left( {ABCD} \right)\) là đường thẳng đi qua \(A\).
Mặt khác, ta có \(BD\parallel \left( P \right)\), \(BD \subset \left( {ABCD} \right)\).
Nên giao tuyến của \(\left( P \right)\) và \(\left( {ABCD} \right)\) là một đường thẳng song song với \(BD\).
Do đường thẳng \(d\) đi qua \(A\) và song song với \(BD\) nên \(d\) chính là giao tuyến của \(\left( P \right)\) và \(\left( {ABCD} \right)\).
Vì hình bình hành \(ABCD\) cố định, nên đường thẳng \(d\) cố định.
Vậy mặt phẳng \(\left( P \right)\) luôn đi qua đường thẳng \(d\) cố định.
Bài toán được chứng minh.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





