HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 6 B├Āi 20 H├Ām sß╗æ m┼® v├Ā h├Ām sß╗æ l├┤garit m├┤n To├Īn hß╗Źc lß╗øp 11 gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng 1 trang 16 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
a) T├Łnh \(y=2^{x}\) khi x lß║¦n lŲ░ß╗Żt nhß║Łn c├Īc gi├Ī trß╗ŗ ŌĆō 1; 0; 1. Vß╗øi mß╗Śi gi├Ī trß╗ŗ cß╗¦a x c├│ bao nhiß╗üu gi├Ī trß╗ŗ cß╗¦a \(y=2^{x}\) tŲ░ŲĪng ß╗®ng?
b) Vß╗øi nhß╗»ng gi├Ī trß╗ŗ n├Āo cß╗¦a x, biß╗āu thß╗®c \(y=2^{x}\), c├│ ngh─®a?
-
Hoß║Īt ─æß╗Öng 2 trang 16 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho h├Ām sß╗æ m┼® \(y=2^{x}\)
a) Ho├Ān th├Ānh bß║Żng gi├Ī trß╗ŗ sau:
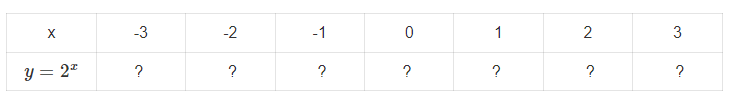
b) Trong mß║Ęt phß║│ng toß║Ī ─æß╗Ö Oxy, biß╗āu diß╗ģn c├Īc ─æiß╗ām (x; y) trong bß║Żng gi├Ī trß╗ŗ ß╗¤ c├óu a. Bß║▒ng c├Īch l├Ām tŲ░ŲĪng tß╗▒, lß║źy nhiß╗üu ─æiß╗ām (\(x;2^{x}\)) vß╗øi \(x\in R\) v├Ā nß╗æi lß║Īi ta ─æŲ░ß╗Żc ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y=2^{x}\).
c) Tß╗½ ─æß╗ō thß╗ŗ ─æ├Ż vß║Į ß╗¤ c├óu b, h├Ży kß║┐t luß║Łn vß╗ü tß║Łp gi├Ī trß╗ŗ v├Ā t├Łnh chß║źt biß║┐n thi├¬n cß╗¦a h├Ām sß╗æ \(y=2^{x}\).
-
Luyß╗ćn tß║Łp 1 trang 17 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Vß║Į ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y=(\frac{3}{2})^{^{x}}\)
-
Hoß║Īt ─æß╗Öng 3 trang 18 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
a) T├Łnh \(y=\log_{2}x\) khi x lß║¦n lŲ░ß╗Żt nhß║Łn c├Īc gi├Ī trß╗ŗ 1; 2; 4. Vß╗øi mß╗Śi gi├Ī trß╗ŗ cß╗¦a x > 0 c├│ bao nhi├¬u gi├Ī trß╗ŗ cß╗¦a \(y=\log_{2}x\) tŲ░ŲĪng ß╗®ng?
b) Vß╗øi nhß╗»ng gi├Ī trß╗ŗ n├Āo cß╗¦a x, biß╗āu thß╗®c \(y=\log_{2}x\) c├│ ngh─®a?
-
Giß║Żi C├óu hß╗Åi trang 18 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Trong c├Īc h├Ām sß╗æ sau, nhß╗»ng h├Ām sß╗æ n├Āo l├Ā h├Ām sß╗æ l├┤garit? Khi ─æ├│ h├Ży chß╗ē ra cŲĪ sß╗æ.
a)\(y=\log_{\sqrt{3}}x\)
b)\(y=\log_{\sqrt{2^{-2}}}x\)
c)\(y=\log_{x}2 \)
d)\(y=\log_{\frac{1}{x}}5\)
-
Hoß║Īt ─æß╗Öng 4 trang 18 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho h├Ām sß╗æ l├┤garit \(y=log_{2}x\)
a) Ho├Ān th├Ānh bß║Żng gi├Ī trß╗ŗ sau:

b) Trong mß║Ęt phß║│ng toß║Ī ─æß╗Ö Oxy, biß╗āu diß╗ģn c├Īc ─æiß╗ām (x; y) trong bß║Żng gi├Ī trß╗ŗ ß╗¤ c├óu a. Bß║▒ng c├Īch l├Ām tŲ░ŲĪng tß╗▒, lß║źy nhiß╗üu ─æiß╗ām (x; \(log_{2}x\)) v├Ā nß╗æi lß║Īi ta ─æŲ░ß╗Żc ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y=log_{2}x\).
c) Tß╗½ ─æß╗ō thß╗ŗ ─æ├Ż vß║Į ß╗¤ c├óu b, h├Ży kß║┐t luß║Łn vß╗ü tß║Łp gi├Ī trß╗ŗ v├Ā t├Łnh chß║źt biß║┐n thi├¬n cß╗¦a h├Ām sß╗æ \(y=log_{2}x\)
-
Vß║Łn dß╗źng trang 19 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Sß╗▒ t─āng trŲ░ß╗¤ng d├ón sß╗æ ─æŲ░ß╗Żc Ų░ß╗øc t├Łnh theo c├┤ng thß╗®c t─āng trŲ░ß╗¤ng m┼® sau:
\(A=Pe^{rt}\)
trong ─æ├│ P l├Ā d├ón sß╗æ cß╗¦a n─ām lß║źy l├Ām mß╗æc, A l├Ā d├ón sß╗æ sau th─ām, r l├Ā tß╗ē lß╗ć t─āng d├ón sß╗æ hß║▒ng n─ām.Biß║┐t rß║▒ng v├Āo n─ām 2020, d├ón sß╗æ Viß╗ćt Nam l├Ā khoß║Żng 97,34 triß╗ću ngŲ░ß╗Øi v├Ā tß╗ē lß╗ć t─āng d├ón sß╗æ l├Ā 0,91% (theo danso.org). Nß║┐u tß╗ē lß╗ć t─āng d├ón sß╗æ n├Āy giß╗» nguy├¬n, h├Ży Ų░ß╗øc t├Łnh d├ón sß╗æ Viß╗ćt Nam v├Āo n─ām 2050.
-
Giß║Żi B├Āi 6.15 trang 19 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Vß║Į ─æß╗ō thß╗ŗ c├Īc h├Ām sß╗æ sau:
a) \(y=3^{x}\)
b) \(y=(\frac{1}{3})^{x}\)
-
Giß║Żi B├Āi 6.16 trang 19 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Vß║Į ─æß╗ō thß╗ŗ cß╗¦a c├Īc h├Ām sß╗æ sau :
a) \(y=\log_{}x\)
b) \(y=\log_{\frac{1}{3}}x\)
-
Giß║Żi B├Āi 6.17 trang 19 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
T├¼m tß║Łp x├Īc ─æß╗ŗnh cß╗¦a c├Īc h├Ām sß╗æ sau:
a) \(y=\log_{}\left | x+3 \right | \)
b) \(y=\ln_{}(4-x^{2})\)
-
Giß║Żi B├Āi 6.18 trang 19 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Ż sß╗Ł mß╗Öt chß║źt ph├│ng xß║Ī bß╗ŗ ph├ón r├Ż theo c├Īch sao cho khß╗æi lŲ░ß╗Żng m(t) cß╗¦a chß║źt c├▓n lß║Īi (t├Łnh bß║▒ng kil├┤gam) sau t ng├Āy ─æŲ░ß╗Żc cho bß╗¤i h├Ām sß╗æ \(13e^{-0,015t}\)
a) T├¼m khß╗æi lŲ░ß╗Żng cß╗¦a chß║źt ─æ├│ tß║Īi thß╗Øi ─æiß╗ām t = 0.
b) Sau 45 ng├Āy khß╗æi lŲ░ß╗Żng chß║źt ─æ├│ c├▓n lß║Īi l├Ā bao nhi├¬u?
-
Giß║Żi B├Āi 6.19 trang 19 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Trong mß╗Öt nghi├¬n cß╗®u, mß╗Öt nh├│m hß╗Źc sinh ─æŲ░ß╗Żc cho xem c├╣ng mß╗Öt danh s├Īch c├Īc lo├Āi ─æß╗Öng vß║Łt v├Ā ─æŲ░ß╗Żc kiß╗ām tra lß║Īi xem hß╗Ź c├▓n nhß╗ø bao nhi├¬u phß║¦n tr─ām danh s├Īch ─æ├│ sau mß╗Śi th├Īng. Giß║Ż sß╗Ł sau t th├Īng, khß║Ż n─āng nhß╗ø trung b├¼nh cß╗¦a nh├│m hß╗Źc sinh ─æ├│ ─æŲ░ß╗Żc t├Łnh theo c├┤ng thß╗®c \(M(t)=75-20ln(t+1),0\leq t\leq 12\) (─æŲĪn vß╗ŗ: %). H├Ży t├Łnh khß║Ż n─āng nhß╗ø trung b├¼nh cß╗¦a nh├│m hß╗Źc sinh ─æ├│ sau 6 th├Īng.
-
Ba╠Ći t├ó╠Żp 6.21 trang 14 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Vß║Į ─æß╗ō thß╗ŗ cß╗¦a c├Īc h├Ām sß╗æ m┼® sau:
a) \(y = {(\sqrt 3 )^x}\);
b) \(y = {\left( {\frac{1}{4}} \right)^x}\).
-
Ba╠Ći t├ó╠Żp 6.22 trang 14 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Vß║Į ─æß╗ō thß╗ŗ cß╗¦a c├Īc h├Ām sß╗æ l├┤garit sau:
a) \({\rm{lo}}{{\rm{g}}_{\sqrt 3 }}x\)
b) \(y = {\rm{lo}}{{\rm{g}}_{\frac{2}{3}}}x\)
-
Ba╠Ći t├ó╠Żp 6.23 trang 14 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho h├Ām sß╗æ m┼® \(f\left( x \right) = {a^x}(a > 0)\). Chß╗®ng minh rß║▒ng:
a) \(\frac{{f\left( {x + 1} \right)}}{{f\left( x \right)}} = a\);
b) \(f\left( { - x} \right) = \frac{1}{{f\left( x \right)}}\);
c) \(f\left( {{x_1} + {x_2}} \right) = f\left( {{x_1}} \right) \cdot f\left( {{x_2}} \right)\).
-
Ba╠Ći t├ó╠Żp 6.24 trang 14 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
T├¼m tß║Łp x├Īc ─æß╗ŗnh cß╗¦a c├Īc h├Ām sß╗æ sau:
a) \(y = {\rm{lo}}{{\rm{g}}_3}\left( {x + 1} \right)\);
b) \(y = {\rm{lo}}{{\rm{g}}_{\frac{1}{2}}}\left| {x - 1} \right|\).
-
Ba╠Ći t├ó╠Żp 6.25 trang 14 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Cho h├Ām sß╗æ l├┤garit \(f\left( x \right) = {\rm{lo}}{{\rm{g}}_a}x\,\,\,\,(0 < a \ne 1)\). Chß╗®ng minh rß║▒ng:
a) \(f\left( {\frac{1}{x}} \right) = - f\left( x \right)\)
b) \(f\left( {{x^\alpha }} \right) = \alpha f\left( x \right)\)
-
Ba╠Ći t├ó╠Żp 6.26 trang 14 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ta ─æß╗ŗnh ngh─®a c├Īc h├Āß╣ā sin hyperbolic v├Ā h├Ām c├┤sin hyperbolic nhŲ░ sau: \({\rm{sinh}}x = \frac{1}{2}\left( {{e^x} - {e^{ - x}}} \right);{\rm{cosh}}x = \frac{1}{2}\left( {{e^x} + {e^{ - x}}} \right)\). Chß╗®ng minh rß║▒ng:
a) \({\rm{sinh}}x\) l├Ā h├Ām sß╗æ lß║╗;
b) \({\rm{cosh}}x\) l├Ā h├Ām sß╗æ chß║Ąn;
c) \({({\rm{cosh}}x)^2} - {({\rm{sinh}}x)^2} = 1\) vß╗øi mß╗Źi \(x\).
-
Ba╠Ći t├ó╠Żp 6.27 trang 15 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Nß║┐u mß╗Öt ├┤ k├Łnh ng─ān khoß║Żng \(3{\rm{\% }}\) ├Īnh s├Īng truyß╗ün qua n├│ th├¼ phß║¦n tr─ām ├Īnh s├Īng \(\rho \) truyß╗ün qua \(n\) ├┤ k├Łnh li├¬n tiß║┐p ─æŲ░ß╗Żc cho gß║¦n ─æ├║ng bß╗¤i h├Ām sß╗æ sau: \(p\left( n \right) = 100 \cdot {(0,97)^n}\).
a) C├│ bao nhi├¬u phß║¦n tr─ām ├Īnh s├Īng sß║Į truyß╗ün qua 10 ├┤ k├Łnh?
b) C├│ bao nhi├¬u phß║¦n tr─ām ├Īnh s├Īng sß║Į truyß╗ün qua 25 ├┤ k├Łnh? (Kß║┐t quß║Ż ß╗¤ c├óu a v├Ā c├óu b ─æß╗▒ŲĪc l├Ām tr├▓n ─æß║┐n h├Āng ─æŲĪn vß╗ŗ).
-
Ba╠Ći t├ó╠Żp 6.28 trang 15 SBT Toa╠ün 15 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Sß╗æ tiß╗ün ban ─æß║¦u 120 triß╗ću ─æß╗ōng ─æŲ░ß╗Żc gß╗Łi tiß║┐t kiß╗ćm vß╗øi l├Żi suß║źt n─ām kh├┤ng ─æß╗Ģi l├Ā \(6{\rm{\% }}\). T├Łnh sß╗æ tiß╗ün (cß║Ż vß╗æn lß║½n l├Żi) thu ─æŲ░ß╗Żc sau 5 n─ām nß║┐u n├│ ─æŲ░ß╗Żc t├Łnh l├Żi k├®p:
a) hß║▒ng qu├Į;
b) hß║▒ng th├Īng;
c) li├¬n tß╗źc.
(Kß║┐t quß║Ż ─æŲ░ß╗Żc t├Łnh theo ─æŲĪn vß╗ŗ triß╗ću ─æß╗ōng v├Ā l├Ām tr├▓n ─æß║┐n chß╗» sß╗æ thß║Łp ph├ón thß╗® ba).
-
Ba╠Ći t├ó╠Żp 6.29 trang 15 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Chu ki b├Īn r├Ż cß╗¦a ─æß╗ōng vß╗ŗ ph├│ng xß║Ī Radi 226 l├Ā khoß║Żng 1600 n─ām. Giß║Ż sß╗Ł khß╗æi lŲ░ß╗Żng \(m\) (t├Łnh bß║▒ng gam) c├▓n lß║Īi sau \(t\) n─ām cß╗¦a mß╗Öt lŲ░ß╗Żng Radi 226 ─æŲ░ß╗Żc cho bß╗¤i c├┤ng thß╗®c: \(m = 25 \cdot {\left( {\frac{1}{2}} \right)^{\frac{t}{{1600}}}}\).
a) Khß╗æi lŲ░ß╗Żng ban ─æß║¦u (khi \(t = 0\)) cß╗¦a lŲ░ß╗Żng Radi 226 ─æ├│ l├Ā bao nhi├¬u?
b) Sau 2500 n─ām khß╗æi lŲ░ß╗Żng cß╗¦a lŲ░ß╗Żng Radi 226 ─æ├│ l├Ā bao nhi├¬u?
-
Ba╠Ći t├ó╠Żp 6.30 trang 15 SBT Toa╠ün 11 T├ó╠Żp 2 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Trong Vß║Łt l├Ł, mß╗®c cŲ░ß╗Øng ─æß╗Ö ├óm (t├Łnh bß║▒ng deciben, k├Ł hiß╗ću l├Ā dB) ─æŲ░ß╗Żc t├Łnh bß╗¤i c├┤ng thß╗®c \(L = 10{\rm{log}}\frac{I}{{{I_0}}}\), trong ─æ├│ \(I\) l├Ā cŲ░ß╗Øng ─æß╗Ö ├óm t├Łnh theo W/m┬▓ v├Ā \({I_0} = {10^{ - 12}}{\rm{\;W}}/{{\rm{m}}^2}\) l├Ā cŲ░ß╗Øng ─æß╗Ö ├óm chuß║®n, tß╗®c l├Ā cŲ░ß╗Øng ─æß╗Ö ├óm thß║źp nhß║źt m├Ā tai ngŲ░ß╗Øi c├│ thß╗ā nghe ─æŲ░ß╗Żc.
a) T├Łnh mß╗®c cŲ░ß╗Øng ─æß╗Ö ├óm cß╗¦a mß╗Öt cuß╗Öc tr├▓ chuyß╗ćn b├¼nh thŲ░ß╗Øng c├│ cŲ░ß╗Øng ─æß╗Ö ├óm l├Ā \({10^{ - 7}}{\rm{\;W}}/{{\rm{m}}^2}\)?
b) Khi cŲ░ß╗Øng ─æß╗Ö ├óm t─āng l├¬n 1000 lß║¦n th├¼ mß╗®c cŲ░ß╗Øng ─æß╗Ö ├óm (─æß║Īi lŲ░ß╗Żng ─æß║Ęc trŲ░ng cho ─æß╗Ö to nhß╗Å cß╗¦a ├óm) thay ─æß╗Ģi thß║┐ n├Āo?






