Hướng dẫn Giải bài tập Toán 11 Kết nối tri thức Chương 4 Bài 11 Hai đường thẳng song song môn Toán học lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Mở đầu trang 78 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?
-
Hoạt động 1 trang 78 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Quan sát bốn tuyến đường trong Hình 4.13 và trả lời câu hỏi sau:
a) Hai tuyến đường nào giao nhau?
b) Hai tuyến đường nào không giao nhau?
c) Hai tuyến đường nào song song?

-
Giải Câu hỏi trang 79 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.

-
Luyện tập 1 trang 79 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17).
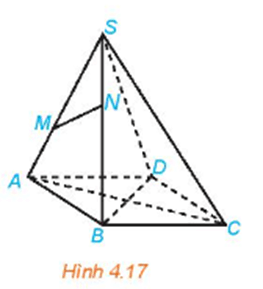
a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng SA, MN, AB có hai đường thẳng nào chéo nhau hay không?
-
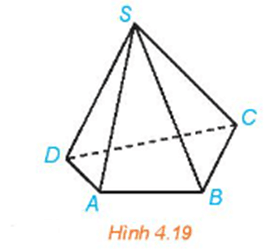
Luyện tập 2 trang 80 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Trong hình chóp tứ giác S.ABCD (H.4.19), chỉ ra những đường thẳng:
a) Chéo với đường thẳng SA;
b) Chéo với đường thẳng BC.
-
Vận dụng 1 trang 80 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?

-
Hoạt động 2 trang 80 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.
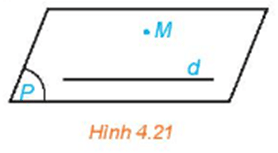
a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?
-
Hoạt động 3 trang 80 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?
-
Luyện tập 3 trang 81 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Trong Ví dụ 1, chứng minh rằng 4 điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.
-
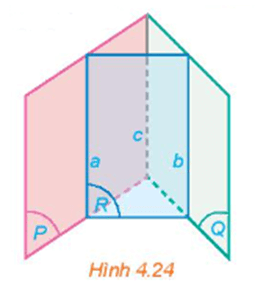
Hoạt động 4 trang 81 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo giao tuyến a và b khác c
a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.
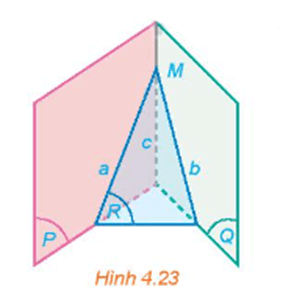
b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao.
-
Luyện tập 4 trang 82 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)
-
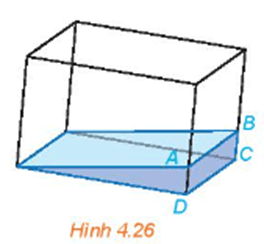
Vận dụng 2 trang 82 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Một bể kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bể nước.
-
Giải Bài 4.9 trang 82 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Trong không gian, cho ba đường thẳng a, b, c. Những mệnh đề nào sau đây là đúng?
a) Nếu a và b không cắt nhau thì a và b song song.
b) Nếu b và c chéo nhau thì b và c không cùng thuộc một mặt phẳng.
c) Nếu a và b cùng song song với c thì a song song với b.
d) Nếu a và b cắt nhau, b và c cắt nhau thì a và c cắt nhau.
-
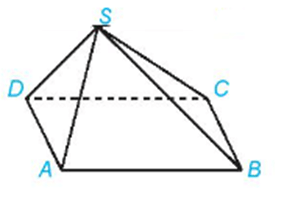
Giải Bài 4.10 trang 82 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thẳng nào song song, cặp đường thẳng nào chéo nhau?
a) AB và CD;
b) AC và BD;
c) SB và CD.
-
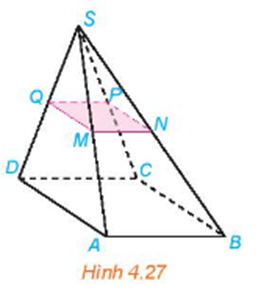
Giải Bài 4.11 trang 82 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành.
-
Giải Bài 4.12 trang 82 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang.
-
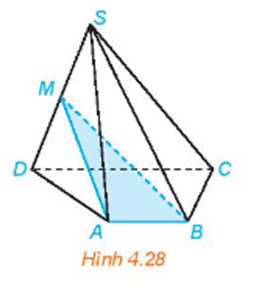
Giải Bài 4.13 trang 82 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).
a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).
b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.
-
Giải Bài 4.14 trang 83 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC.
a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD).
b) Chứng minh rằng d song song với BD.
-
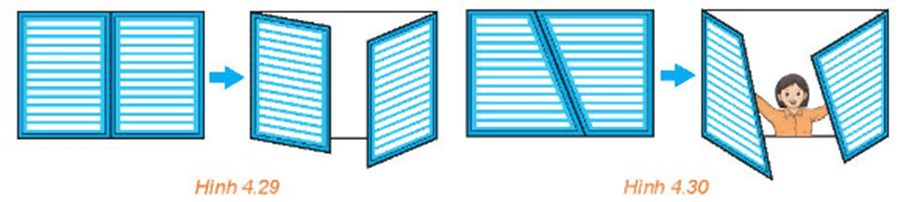
Giải Bài 4.15 trang 83 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
(Đố vui) Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao.
Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì có vị trí nào của hai cánh cửa để hai mép ngoài của chúng song song với nhau hay không?
-
Bài tập 4.13 trang 59 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP) trong các trường hợp sau:
a) Đường thẳng NP song song với đường thẳng BD.
b) Đường thẳng NP cắt BD.
-
Bài tập 4.14 trang 59 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là một điểm bất kì thuộc cạnh SC.
a) Xác định các giao tuyến của mặt phẳng (MAB với các mặt của hình chóp.
b) Xác định các giao tuyến của mặt phẳng (MAD với các mặt của hình chóp.
-
Bài tập 4.15 trang 59 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi M, N lần lượt là các điểm thuộc các cạnh SA, SD.
a) Xác định giao tuyến d của hai mặt phẳng (MCD) và (NAB).
b) Chứng minh rằng d // AB.
-
Bài tập 4.16 trang 59 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Xác định giao tuyến của hai mặt phẳng (ANP) và (CMQ).
b) Xác định giao tuyến của hai mặt phẳng (ANP) và (ABD).
c) Xác định giao tuyến của hai mặt phẳng (CMQ) và (BCD).
d) Chứng minh rằng các giao tuyến ở trên đôi một song song với nhau.
-
Bài tập 4.17 trang 59 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng GH, CE, DF đôi một song song?
-
Bài tập 4.18 trang 59 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi E, F lần lượt là trọng tâm của các tam giác SAD, SBC.
a) Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Chứng minh rằng EF//MN, từ đó suy ra EF//AB.
b) Xác định các giao tuyến của mặt phẳng (AEF) với các mặt của hình chóp.
c) Trong các giao tuyến tìm được ở câu b, giao tuyến nào song song với đường thẳng EF?
-
Bài tập 4.19 trang 60 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.
a) Chứng minh rằng các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
b) Chứng minh rằng các đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.
-
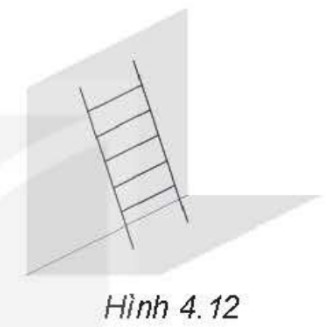
Bài tập 4.20 trang 60 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Một chiếc thang được đặt sao cho hai đầu của chân thang dựa vào tường, hai đầu còn lại nằm trên sàn nhà (H. 4.12). Biết rằng chiếc thang có dạng hình chữ nhật, hãy giải thích vì sao hai đầu của chân thang nằm trên sàn nhà lại cách đều chân tường?
-
Bài tập 4.21 trang 60 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bạn Hà lấy một tờ giấy hình chữ nhật và gấp tờ giấy sao cho hai mép của tờ giấy song song với nhau (H.4.13). Hà thấy rằng dù gấp thế nào thì đường nếp gấp vẫn luôn song song với hai mép của tờ giấy. Hãy giải thích vì sao?







