Bài tập 49 trang 124 SGK Toán 11 NC
Cho dãy hình vuông H1, H2, …, Hn,… Với mỗi số nguyên dương n, gọi un, pn và Sn lần lượt là độ dài cạnh, chu vi và diện tích của hình vuông Hn.
a. Giả sử dãy số (un) là một cấp số cộng với công sai khác 0. Hỏi khi đó các dãy số (pn) và (Sn) có phải là các cấp số cộng hay không ? Vì sao ?
b. Giả sử dãy số (un) là một cấp số nhân với công bội dương. Hỏi khi đó các dãy số (pn) và (Sn) có phải là các cấp số nhân hay không ? Vì sao ?
Hướng dẫn giải chi tiết
a) Theo giả thiết ta c :
pn = 4un và \(S_n=u_n^2\) với mọi n ∈ N∗
a) Gọi d là công sai của cấp số cộng (un), d ≠ 0. Khi đó với mọi n ∈ N∗, ta có:
pn+1−pn = 4(un+1−un) = 4d (không đổi)
Vậy (pn) là cấp số cộng.
Sn+1−Sn = (un+1−un)(un+1+un) = d.(un+1+un) không là hằng số (do d ≠ 0)
Vậy (Sn) không là cấp số cộng.
b) Gọi q là công bội của cấp số nhân (un), q > 0. Khi đó với mọi n ∈ N∗, ta có:
\(\frac{{{p_{n + 1}}}}{{{p_n}}} = \frac{{4{u_{n + 1}}}}{{4{u_n}}} = q\) (không đổi)
\(\frac{{{S_{n + 1}}}}{{{S_n}}} = \frac{{u_{n + 1}^2}}{{u_n^2}} = {q^2}\) (không đổi)
Từ đó suy ra các dãy số (pn) và (Sn) là cấp số nhân.
-- Mod Toán 11 HỌC247
-


Cho 4 số a, b, c, d theo thứ tự lập nên cấp số cộng và các số a-2, b-6, c-7, d-2 theo thứ tự lập nên cấp số nhân. Tính a, b, c, d
bởi phuong uyen
 02/05/2020
Theo dõi (0) 0 Trả lời
02/05/2020
Theo dõi (0) 0 Trả lời -


Tìm \(u_1\) và d?
bởi ainn
 15/04/2020
15/04/2020
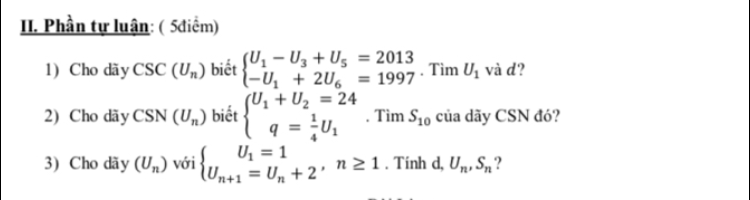 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Viết 6 số hạng đầu của dãy số Un=(n+1)/n
bởi Duck
 02/04/2020
02/04/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Biết rằng tồn tại đúng hai giá trị của tham số mm để phương trình x3−7x2 2(m2 6m)x−8=0x3−7x2 2(m2 6m)x−8=0 có ba nghiệm phân biệt lập thành một cấp số nhân. Tính tổng lập phương của hai giá trị đó.
bởi Dong Nanda
 25/03/2020
Giúp em với ạTheo dõi (0) 1 Trả lời
25/03/2020
Giúp em với ạTheo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 47 trang 123 SGK Toán 11 NC
Bài tập 48 trang 123 SGK Toán 11 NC
Bài tập 50 trang 124 SGK Toán 11 NC
Bài tập 51 trang 124 SGK Toán 11 NC
Bài tập 52 trang 125 SGK Toán 11 NC
Bài tập 53 trang 125 SGK Toán 11 NC
Bài tập 54 trang 125 SGK Toán 11 NC
Bài tập 55 trang 125 SGK Toán 11 NC





