Bài tập 50 trang 124 SGK Toán 11 NC
Cho dãy số (un) xác định bởi:
u1 = 3 và \({u_{n + 1}} = \sqrt {{u_n} + 6} \) với mọi n ≥ 1
Chứng minh rằng (un) vừa là cấp số cộng, vừa là cấp số nhân.
Hướng dẫn giải chi tiết
Ta chứng minh un = 3 (1) với mọi n bằng qui nạp
- Với n = 1 ta có u1 = 3 ⇒ (1) đúng
- Giả sử (1) đúng với n = k, tức là uk = 3
- Ta chứng minh uk+1 = 3
Thật vậy, ta có: \({u_{k + 1}} = \sqrt {{u_k} + 6} = \sqrt {3 + 6} = 3\)
Vậy un = 3, ∀n ≥ 1 do đó (un) vừa là cấp số cộng công sai d = 0 vừa là cấp số nhân công bội q = 1.
-- Mod Toán 11 HỌC247
-


Tính giới hạn (∛4x-2)/(x-2) khi x->2
bởi Lại Thị Ngọc Diễm
 18/03/2020
Giúp mình với
18/03/2020
Giúp mình với Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Giải dùm
Giải dùm Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính lim [4*2^(n+3)-4*5^(n+1)]/[3^(n+2)+5^n]
bởi Hồng Ngọc
 01/03/2020
01/03/2020
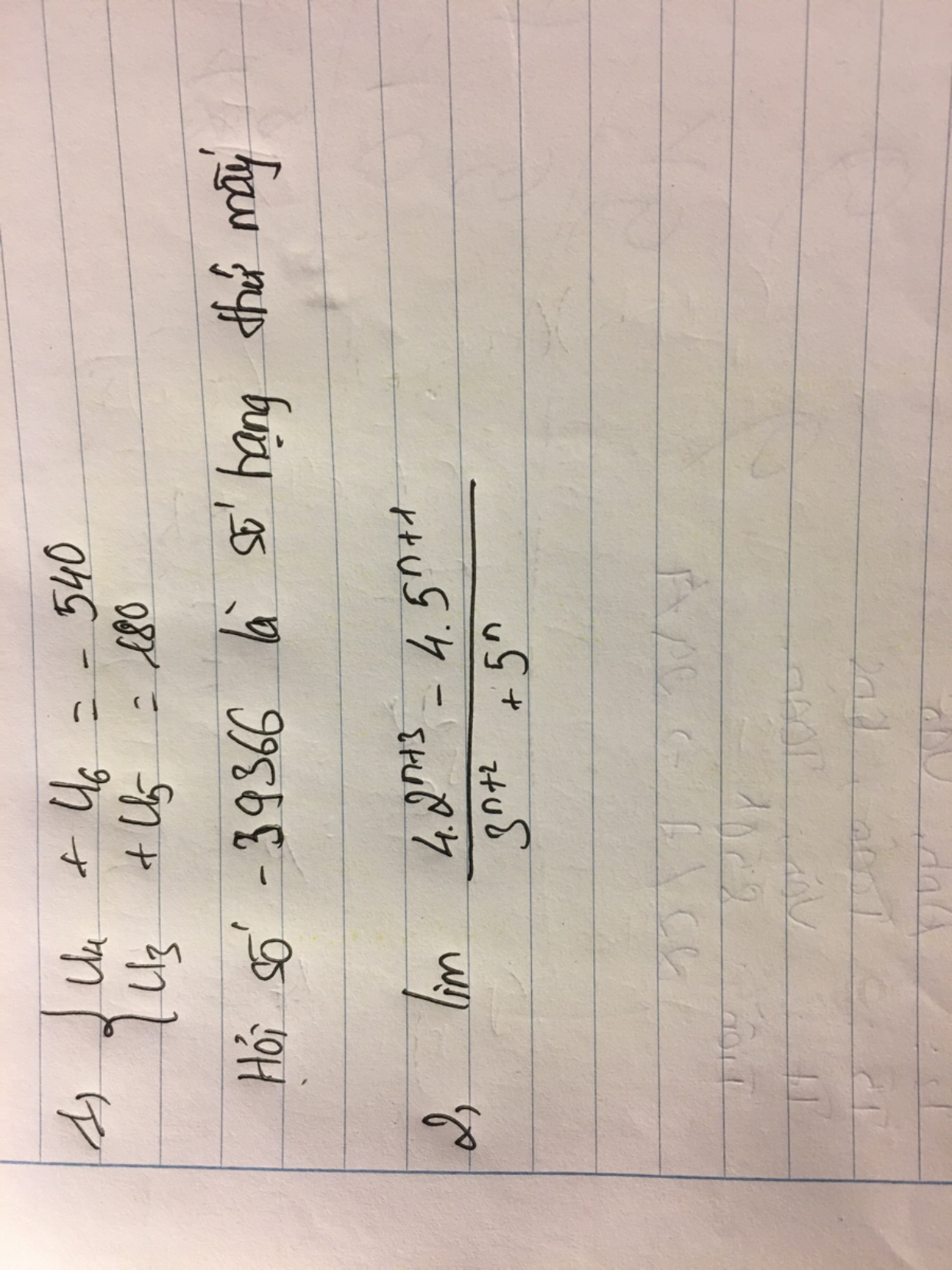 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Xác định số hạng đầu, công sai và số hạng thứ n của các cấp số cộng sau
bởi Bùi Thị Ngọc Trang
 17/02/2020
17/02/2020
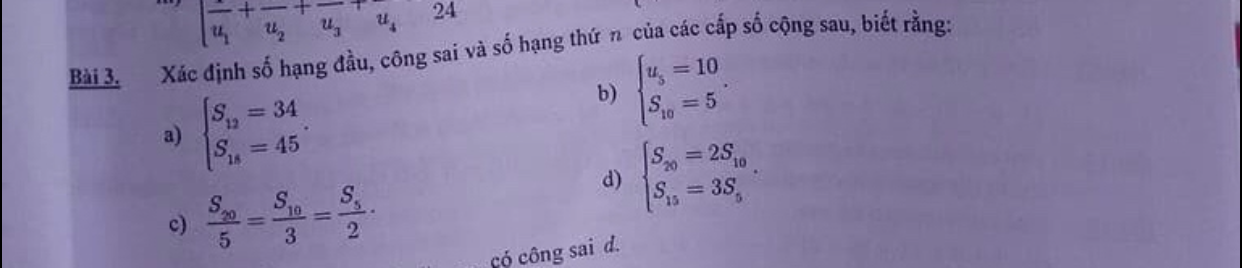 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời





