Luyện tập 2 trang 36 SGK Toán 10 Kết nối tri thức tập 1
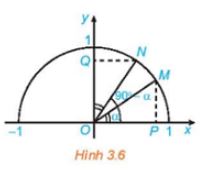
Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chứng mình rằng \(\Delta MOP = \Delta NOQ\). Từ đó nêu mối quan hệ giữa \(\cos \alpha \) và \(\sin \left( {{{90}^o} - \alpha } \right)\).
Hướng dẫn giải chi tiết
Phương pháp giải
Nhận xét vị trí của M và N trong mỗi trường hợp: \(\alpha = {90^o};\;\alpha < {90^o}\)
Khi \({0^o} < \alpha < {90^o}\): \(\cos \alpha ,\;\sin \alpha \) tương ứng là hoành độ và tung độ của điểm M.
Hướng dẫn giải
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)
-- Mod Toán 10 HỌC247
-


Chứng minh rằng trong tam giác ABC ta có: \(\tan B = - \tan \left( {A + C} \right)\)
bởi Co Nan
 27/11/2022
Theo dõi (0) 1 Trả lời
27/11/2022
Theo dõi (0) 1 Trả lời -


Tìm góc \(\alpha \left( {0^\circ \le \alpha \le 180^\circ } \right)\) trong trường hợp sau: \(\cot \alpha = - 1\)
bởi Thiên Mai
 27/11/2022
Theo dõi (0) 1 Trả lời
27/11/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Luyện tập 1 trang 35 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 2 trang 36 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Vận dụng trang 37 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.1 trang 37 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.2 trang 37 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.3 trang 37 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.4 trang 37 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.1 trang 32 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.2 trang 32 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.3 trang 33 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.4 trang 33 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.5 trang 34 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 3.6 trang 34 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

.JPG)
.JPG)




