Hoạt động khám phá 2 trang 34 SGK Toán 10 Chân trời sáng tạo tập 1
Cho hệ bất phương trình: \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\end{array} \right.\)
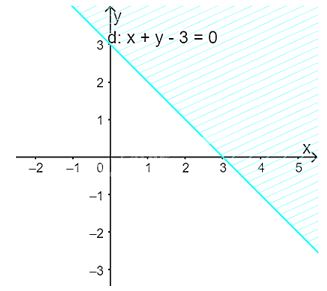
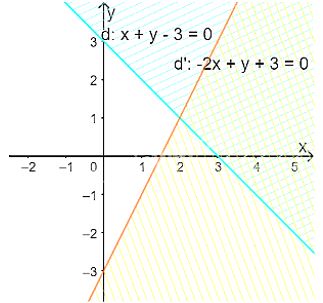
Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho?
Hướng dẫn giải chi tiết Hoạt động khám phá 2
Phương pháp giải
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên cùng một mặt phẳng Oxy
Lời giải chi tiết
Vẽ đường thẳng \(d:x + y - 3 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( {1;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 0 - 3 = - 3 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(d\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Vẽ đường thẳng \(d': - 2x + y + 3 = 0\) đi qua hai điểm \(A(1; - 1)\) và \(B\left( {2;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 + 3 = 3 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d'\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.
-- Mod Toán 10 HỌC247
-


Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 5}\\{3x + 2y \le 12}\\{x \ge 1}\\{y \ge 0}\end{array}} \right.\left( {III} \right)\)
bởi Nguyen Dat
 17/11/2022
Theo dõi (0) 1 Trả lời
17/11/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Hoạt động khám phá 1 trang 33 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 34 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 35 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 37 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 37 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 38 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 38 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 38 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 38 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 33 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 33 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 33 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 34 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST