Giải bài 9 trang 100 SGK Toán 10 Cánh diều tập 1
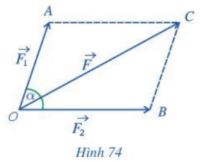
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc \((\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = \alpha \) làm cho vật di chuyển theo hướng từ O đến C (Hình 74). Lập công thức tính cường độ của hợp lực \(\overrightarrow F \) làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) làm cho vật di chuyển).
Hướng dẫn giải chi tiết
Phương pháp giải
+) OACB là hình bình hành thì \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \)
+) Tính cường độ của hợp lực \(\overrightarrow F \) bằng định lí cosin: \(O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A\)
Hướng dẫn giải
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{l}\quad \;O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A\\ \Leftrightarrow O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos ({180^o} - \alpha )\\ \Leftrightarrow \left| {\overrightarrow F } \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} - 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos ({{180}^o} - \alpha )} \end{array}\)
\(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)
-- Mod Toán 10 HỌC247
-


Thực hiện tính: \(\cosα,\) nếu \(\tan \alpha = 2\sqrt 2 ,\pi < \alpha < {{3\pi } \over 2}.\)
bởi Nguyễn Vũ Khúc
 29/08/2022
Theo dõi (0) 1 Trả lời
29/08/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Giải bài 7 trang 100 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 8 trang 100 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 67 trang 106 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 68 trang 106 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 69 trang 106 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 70 trang 106 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 71 trang 106 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 72 trang 107 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 73 trang 107 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 74 trang 107 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 75 trang 107 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 76 trang 107 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 77 trang 107 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 78 trang 107 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 79 trang 108 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 80 trang 108 SBT Toán 10 Cánh diều tập 1 - CD