Giải bài 4.22 trang 58 SBT Toán 10 Kết nối tri thức tập 1
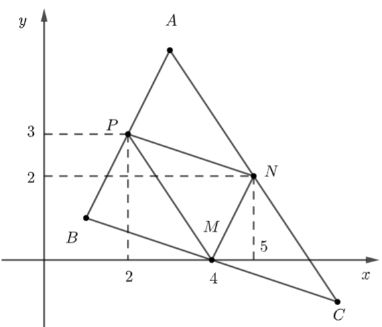
Trong mặt phẳng tọa độ \(Oxy\) cho ba điểm \(M(4;0),\,\,N(5;2)\) và \(P(2;3).\) Tìm tọa độ các đỉnh của tam giác \(ABC,\) biết \(M,\,\,N,\,\,P\) theo thứ tự là trung điểm các cạnh \(BC,\,\,CA,\,\,AB.\)
Hướng dẫn giải chi tiết Bài 4.22
Phương pháp giải
Cho hai vectơ \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x;y} \right)\). Khi đó:
\(\begin{array}{*{20}{l}}
{*\vec u + \vec v = \left( {x + x';y + y'} \right);}\\
{*\vec u - \vec v = \left( {x - x';y - y'} \right);}\\
{*k\vec u = \left( {kx;ky} \right),k \in R}
\end{array}\)
Lời giải chi tiết
Ta có: \(MN,\,\,NP,\,\,MP\) là đường trung bình của \(\Delta ABC\)
\( \Rightarrow \) \(MN\)//\(AB\), \(NP\)//\(BC\), \(MP\)//\(AC\).
\( \Rightarrow \) \(APMN\), \(BPNM\), \(CMPN\) là hình bình hành
Xét hình bình hành \(APMN\) có:
\(\begin{array}{l}\overrightarrow {OA} = \overrightarrow {OP} + \overrightarrow {ON} - \overrightarrow {OM} \\ \Rightarrow \overrightarrow {OA} = (2;3) + (5;2) - (4;0) = (3;5)\end{array}\)
\( \Rightarrow \) Tọa độ điểm \(A\) là: \(A(3;5).\)
Xét hình bình hành \(BPNM\) có:
\(\begin{array}{l}\overrightarrow {OB} = \overrightarrow {OP} + \overrightarrow {OM} - \overrightarrow {ON} \\ \Rightarrow \overrightarrow {OB} = (2;3) + (4;0) - (5;2) = (1;1)\end{array}\)
\( \Rightarrow \) Tọa độ điểm \(B\) là: \(B(1;1).\)
Xét hình bình hành \(CMPN\) có:
\(\begin{array}{l}\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {OM} - \overrightarrow {OP} \\ \Rightarrow \overrightarrow {OC} = (5;2) + (4;0) - (2;3) = (7; - 1)\end{array}\)
\( \Rightarrow \) Tọa độ điểm \(C\) là: \(C(7; - 1).\)
-- Mod Toán 10 HỌC247
-


Trên trục \((0;\overrightarrow e )\) cho các điểm \(A, B, M,N\) có tọa độ lần lượt là \(-1, 2, 3, -2\). Hãy tính độ dài đại số của \(\overrightarrow {AB} \) và \(\overrightarrow {MN} \). Từ đó suy ra hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {MN} \) ngược hướng.
bởi minh thuận
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Giải bài 4.19 trang 65 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.19 trang 65 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.23 trang 58 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.24 trang 58 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.25 trang 59 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.26 trang 59 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.27 trang 59 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.28 trang 59 SBT Toán 10 Kết nối tri thức tập 1 - KNTT