Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 473757
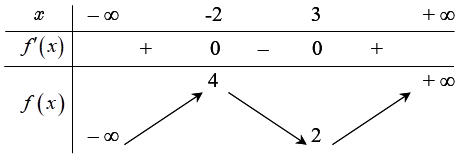
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng nào?
- A. \(\left( {3; + \infty } \right)\).
- B. \(\left( { - \infty ;4} \right)\).
- C. \(\left( {2;4} \right)\).
- D. \(\left( {2; + \infty } \right)\).
-
Câu 2: Mã câu hỏi: 473759
Trong các hàm số dưới đây, hàm số nào đồng biến trên \(\mathbb{R}\)?
- A. \(y={{x}^{3}}+2x+1.\)
- B. \(y=\frac{{{x}^{4}}}{4}+{{x}^{2}}. \)
- C. \(y={{x}^{3}}-2{{x}^{2}}+1. \)
- D. \(y=\frac{2x-1}{x+3}\)
-
Câu 3: Mã câu hỏi: 473764
Cho hàm số \(y=-{{x}^{4}}-2{{x}^{2}}+1\). Khẳng định nào dưới đây đúng?
- A. Hàm số nghịch biến trên khoảng \(\left( -\infty ;\,0 \right)\).
- B. Hàm số nghịch biến trên khoảng \(\left( 0;\,+\infty \right)\).
- C. Hàm số nghịch biến trên khoảng \(\left( -1;1 \right)\).
- D. Hàm số đồng biến trên khoảng \(\left( -1;1 \right)\).
-
Câu 4: Mã câu hỏi: 473766
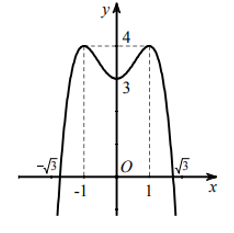
Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình vẽ:
Giá trị cực đại của hàm số đã cho bằng?
- A. 3
- B. 2
- C. 1
- D. 4
-
Câu 5: Mã câu hỏi: 473769
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của \({f}'\left( x \right)\) như sau:
Số điểm cực tiểu của hàm số đã cho bằng?
- A. 1
- B. 2
- C. 3
- D. 0
-
Câu 6: Mã câu hỏi: 473772
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y={{x}^{4}}+\left( \frac{m+2}{m-2} \right){{x}^{2}}+3\) có ba điểm cực trị?
- A. 2
- B. 5
- C. 3
- D. 4
-
Câu 7: Mã câu hỏi: 473773
Cho hàm số f(x) có đạo hàm \({f}'\left( x \right)=x\left( x-1 \right){{\left( x-2 \right)}^{2}}\left( {{x}^{2}}-1 \right), \forall x\in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là?
- A. 3
- B. 2
- C. 1
- D. 0
-
Câu 8: Mã câu hỏi: 473776
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\frac{x-2}{3x-4}\) trên đoạn \(\left[ 2;3 \right]\). Khi đó tổng M + 2m bằng?
- A. \(\frac{1}{5}.\)
- B. \(\frac{17}{2}.\)
- C. \(\frac{11}{2}.\)
- D. 6
-
Câu 9: Mã câu hỏi: 473780
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình:
Khi đó giá trị nhỏ nhất của hàm số \(y=f\left( x \right)\) trên đoạn \(\left[ -10;10 \right]\) bằng bao nhiêu?
- A. \(\frac{14}{3}. \)
- B. -38.
- C. \(\frac{11}{2}.\)
- D. -2
-
Câu 10: Mã câu hỏi: 473783
Phương trình đường tiệm cận ngang của đồ thị hàm số \(y=\frac{1-x}{2x-3}\) là?
- A. \(y=\frac{1}{2}.\)
- B. \(y=\frac{3}{2}.\)
- C. \(y=-\frac{1}{3}.\)
- D. \(y=-\frac{1}{2}.\)
-
Câu 11: Mã câu hỏi: 473787
Cho hàm số y = f(x) có bảng biến thiên sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f(x) là?
- A. 3
- B. 2
- C. 0
- D. 1
-
Câu 12: Mã câu hỏi: 473797
Tìm tổng tất cả các giá trị của tham số m để đồ thị hàm số \(y=\frac{x-1}{\left( x+m \right)\left( x+2 \right)}\) có đúng 2 đường tiệm cận?
- A. 1
- B. 3
- C. -1
- D. 0
-
Câu 13: Mã câu hỏi: 473801
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
- A. \(y=-{{x}^{4}}+2{{x}^{2}}+1.\)
- B. \(y={{x}^{3}}-3{{x}^{2}}-2.\)
- C. \(y=-{{x}^{3}}+4{{x}^{2}}-2. \)
- D. \(y={{x}^{4}}-\frac{{{x}^{2}}}{3}+1.\)
-
Câu 14: Mã câu hỏi: 473802
Cho hàm số \(y=a{{x}^{3}}+3x-d\,\,\left( a;d\in \mathbb{R} \right)\) có đồ thị là đường cong trong hình vẽ:
Mệnh đề nào dưới đây đúng?
- A. a > 0, d > 0.
- B. a < 0, d < 0.
- C. a > 0, d < 0.
- D. a < 0, d > 0.
-
Câu 15: Mã câu hỏi: 473808
Tìm số giao điểm của đồ thị hàm số \(y=-{{x}^{3}}+3{{x}^{2}}+1\) và đường thẳng y = 2x + 1?
- A. 3
- B. 2
- C. 1
- D. 0
-
Câu 16: Mã câu hỏi: 473809
Cho biểu thức \(P=\frac{a\left( {{a}^{-1}}+{{a}^{2}} \right)}{{{a}^{2}}\left( {{a}^{1}}+{{a}^{-2}} \right)}\), với a > 0. Khẳng định nào dưới đây là đúng?
- A. \(P={{a}^{\frac{1}{2}}}.\)
- B. P = 1.
- C. \(P={{a}^{-2}}.\)
- D. P = a.
-
Câu 17: Mã câu hỏi: 473812
Cho a, b, x và y là các số thực dương; a, b khác 1. Khẳng định nào dưới đây là đúng?
- A. \({{\log }_{a}}xy={{\log }_{a}}x.{{\log }_{a}}y\)
- B. \({{\log }_{a}}{{b}^{m}}={{\left( {{\log }_{a}}b \right)}^{m}}\)
- C. \({{\log }_{a}}\frac{x}{y}=\frac{{{\log }_{a}}x}{{{\log }_{a}}y}\)
- D. \({{\log }_{a}}\frac{x}{y}={{\log }_{a}}x-{{\log }_{a}}y\)
-
Câu 18: Mã câu hỏi: 473814
Biết \({{\log }_{4}}5=a\). Tính \({{\log }_{25}}20\) theo a?
- A. \({{\log }_{25}}20=\frac{1}{2a}. \)
- B. \({{\log }_{25}}20=\frac{1+a}{2a}.\)
- C. \({{\log }_{25}}20=\frac{1-a}{2a}. \)
- D. \({{\log }_{25}}20=4a.\)
-
Câu 19: Mã câu hỏi: 473816
Tìm đạo hàm của hàm số sau \(y={{\left( {{x}^{3}}-3x \right)}^{\frac{1}{2}}}\)?
- A. \(\frac{3\left( {{x}^{2}}-1 \right)}{2\sqrt{{{x}^{3}}-3x}}. \)
- B. \(\frac{{{x}^{2}}-1}{2\sqrt{{{x}^{3}}-3x}}. \)
- C. \(\frac{1}{2}.{{\left( {{x}^{3}}-3x \right)}^{\frac{-1}{2}}}.\)
- D. \(\frac{3}{2}.\left( {{x}^{2}}-1 \right).\)
-
Câu 20: Mã câu hỏi: 473822
Tìm tập xác định của hàm số \(y={{\log }_{2023}}\left( x-{{x}^{2}} \right)\)?
- A. \(D=\left( 0;+\infty \right). \)
- B. \(D=\left( -\infty ;0 \right)\cup \left( 1;+\infty \right).\)
- C. \(D=\left( 0;1 \right). \)
- D. \(D=\mathbb{R}.\)
-
Câu 21: Mã câu hỏi: 473832
Trong các hàm số sau hàm số nào nghịch biến trên \(\mathbb{R}\)?
- A. \(y=\log \left( {{x}^{2}}+2 \right).\)
- B. \(y={{\left( \frac{1}{{{e}^{2}}} \right)}^{x}}.\)
- C. \({{\log }_{3}}{{x}^{2}}.\)
- D. \(y={{\left( \frac{1}{\pi } \right)}^{-x}}.\)
-
Câu 22: Mã câu hỏi: 473833
Phương trình \({{\left( \sqrt{3} \right)}^{2-x}}=81\) có nghiệm là?
- A. -6
- B. 6
- C. 2
- D. -2
-
Câu 23: Mã câu hỏi: 473836
Nghiệm của phương trình \({{\log }_{\frac{2}{3}}}\left( x-2 \right)=1\) là?
- A. 2.
- B. \(\frac{8}{3}. \)
- C. \(\frac{1}{3}.\)
- D. \(\frac{-8}{3}.\)
-
Câu 24: Mã câu hỏi: 473842
Phương trình \({{16}^{x+1}}-{{10.2}^{2x+1}}+4=0\) có 2 nghiệm phân biệt là \({{x}_{1}}\) và \({{x}_{2}}\). Tổng \({{x}_{1}}+{{x}_{2}}\) bằng?
- A. -1
- B. \(-\frac{3}{2}.\)
- C. 0
- D. \(\frac{9}{4}.\)
-
Câu 25: Mã câu hỏi: 473849
Gọi S là tập nghiệm của phương trình \(2{{\log }_{3}}\left( 3x-2 \right)+{{\log }_{3}}{{\left( x+2 \right)}^{2}}=2\) trên \(\mathbb{R}\). Tổng các phần tử của S bằng?
- A. \(\frac{10}{3}.\)
- B. 8.
- C. 1.
- D. \(\frac{1+\sqrt{7}}{3}.\)
-
Câu 26: Mã câu hỏi: 473853
Tập nghiệm của bất phương trình \({{3}^{x}}\le 9\) là?
- A. \(\left( -\infty ;1 \right].\)
- B. \(\left( -\infty ;2 \right].\)
- C. \(\left( 0;\frac{1}{2} \right]. \)
- D. \(\left( 0;2 \right].\)
-
Câu 27: Mã câu hỏi: 473859
Tập nghiệm của bất phương trình \(\frac{\ln x+2}{\ln x-1}<0\) là?
- A. \(\left( \frac{1}{{{e}^{2}}};+\infty \right).\)
- B. \(\left( -\infty ;\frac{1}{e} \right)\cup \left( {{e}^{2}};+\infty \right).\)
- C. \(\left( \frac{1}{e};{{e}^{2}} \right).\)
- D. \(\left( \frac{1}{{{e}^{2}}};e \right). \)
-
Câu 28: Mã câu hỏi: 473861
Khối bát diện đều là khối đa diện đều loại nào?
- A. \(\left\{ 3;3 \right\}. \)
- B. \(\left\{ 3;5 \right\}.\)
- C. \(\left\{ 3;4 \right\}.\)
- D. \(\left\{ 4;3 \right\}.\)
-
Câu 29: Mã câu hỏi: 473865
Tổng số mặt và số cạnh của hình chóp ngũ giác là?
- A. 16
- B. 15
- C. 12
- D. 11
-
Câu 30: Mã câu hỏi: 473869
Thể tích V của khối tứ diện có diện tích đáy bằng B và chiều cao bằng h là?
- A. \(V=Bh.\)
- B. \(V=\frac{1}{3}Bh.\)
- C. \(V=\frac{1}{3}{{B}^{2}}h.\)
- D. \(V=\frac{1}{3}B{{h}^{2}}.\)
-
Câu 31: Mã câu hỏi: 473885
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, \(SA\bot \left( ABCD \right)\), \(SA=a\sqrt{3}\). Tính thể tích khối chóp S.ABCD?
- A. \(V={{a}^{3}}\sqrt{3}. \)
- B. \(V=\frac{{{a}^{3}}\sqrt{3}}{3}.\)
- C. \(V={{a}^{3}}. \)
- D. \(V=\frac{{{a}^{3}}}{3}.\)
-
Câu 32: Mã câu hỏi: 473890
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy ABC là tam gác vuông tại \(B,\,\,AB=BC=a và A{A}'=3a\). Thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\) bằng?
- A. \(3{{a}^{3}}.\)
- B. \(\frac{3}{2}{{a}^{3}}.\)
- C. \(\frac{1}{2}{{a}^{3}}.\)
- D. \(2{{a}^{3}}.\)
-
Câu 33: Mã câu hỏi: 473895
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA\bot \left( ABCD \right)\) và SA = 2a. Gọi M là điểm nằm trên cạnh CD. Tính thể tích khối chóp S.ABM theo a?
- A. \frac{3{{a}^{3}}}{4}.
- B. \frac{{{a}^{3}}}{2}.
- C. \frac{2{{a}^{3}}}{3}.
- D. \frac{{{a}^{3}}}{3}.
-
Câu 34: Mã câu hỏi: 473901
Thể tích V khối nón có diện tích đáy bằng \(4\pi \) và chiều cao bằng 3 là?
- A. \(V=4\pi \)
- B. \(V=\frac{4}{3}\pi\)
- C. \(V=12\pi\)
- D. \(V=6\pi \)
-
Câu 35: Mã câu hỏi: 473907
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là 4a và chiều cao là 6a. Thể tích của khối nón có đỉnh S và đáy là đường tròn nội tiếp tứ giác ABCD bằng?
- A. 4\pi {{a}^{3}}.
- B. 8\pi {{a}^{3}}.
- C. 6\pi {{a}^{3}}.
- D. 2\pi {{a}^{3}}.
-
Câu 36: Mã câu hỏi: 473914
Khi quay hình chữ nhật ABCD xung quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Bán kính hình trụ được tạo thành bằng độ dài đoạn thẳng nào dưới đây?
- A. AB
- B. AC
- C. AD
- D. BD
-
Câu 37: Mã câu hỏi: 473917
Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Diện tích toàn phần của hình trụ đã cho bằng?
- A. \(\pi {{a}^{2}}.\)
- B. \(6\pi {{a}^{2}}. \)
- C. \(\frac{3\pi {{a}^{2}}}{2}. \)
- D. \(4\pi {{a}^{2}}.\)
-
Câu 38: Mã câu hỏi: 473924
Cho hình trụ (T) có hai đáy là hai hình tròn (O) và (O'), thiết diện qua trục của hình trụ là hình vuông. Gọi A và B là hai điểm lần lượt nằm trên hai đường tròn (O) và (O'). Biết AB = a và khoảng cách giữa AB và OO' bằng \(\frac{a\sqrt{2}}{2}\). Bán kính đáy của hình trụ (T) bằng?
- A. \(\frac{a\sqrt{6}}{4}.\)
- B. \(\frac{2a\sqrt{2}}{3}. \)
- C. \(\frac{a\sqrt{6}}{2}. \)
- D. \(\frac{a\sqrt{3}}{3}.\)
-
Câu 39: Mã câu hỏi: 473927
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\), đồ thị hàm số \(y={f}'\left( x \right)\) được cho như hình vẽ:
Hàm số \(y=f\left( \left| 2-x \right| \right)\) đồng biến trên khoảng nào?
- A. \(\left( -\infty ;0 \right). \)
- B. \(\left( 0;1 \right).\)
- C. \(\left( 1;2 \right). \)
- D. \(\left( 3;+\infty \right).\)
-
Câu 40: Mã câu hỏi: 473956
Cho hàm số bậc bốn \(y=f\left( x \right)\) có \(f\left( 1 \right)=0\). Biết đồ thị hàm số \(y={f}'\left( x \right)\) được cho như hình:
Xét hàm số \(g\left( x \right)=\left| f\left( 1+\frac{x}{2} \right)+\frac{{{x}^{2}}}{8} \right|\). Đặt M là số điểm cực đại và m là số điểm cực tiểu của hàm số \(g\left( x \right)\). Tính giá trị biểu thức \({{M}^{2}}+{{m}^{2}}\)?
- A. {{M}^{2}}+{{m}^{2}}=13.
- B. {{M}^{2}}+{{m}^{2}}=2.
- C. {{M}^{2}}+{{m}^{2}}=5.
- D. {{M}^{2}}+{{m}^{2}}=25.
-
Câu 41: Mã câu hỏi: 473970
Cho hàm số \(y=-{{x}^{3}}+3{{x}^{2}}+9x+{{k}^{2}},~ k\in \mathbb{R}\). Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ -2;4 \right]\). Biết M + 2m - 20 = 0. Tổng bình phương các giá trị của k thoả mãn yêu cầu đề bài bằng bao nhiêu?
- A. 8
- B. 2
- C. 18
- D. 32
-
Câu 42: Mã câu hỏi: 473971
Cho hàm số \(y=2{{x}^{3}}+b{{x}^{2}}+cx+d\) có đồ thị như hình:
Khẳng định nào sau đây đúng?
- A. b + 2c + 3d = 3.
- B. \({{c}^{2}}-{{d}^{2}}<{{b}^{2}}. \)
- C. bcd = -432.
- D. b + d > c.
-
Câu 43: Mã câu hỏi: 473980
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình:
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(f\left( x \right)=mx+m-3\) có nghiệm thuộc khoảng \(\left( 1;3 \right)\)?
- A. 3
- B. 2
- C. 4
- D. 5
-
Câu 44: Mã câu hỏi: 473990
Cho a > 0, b > 0 thỏa mãn \({{\log }_{30a+24b+21}}\left( 25{{a}^{2}}+4{{b}^{2}}+1 \right)+{{\log }_{\text{20a}b+1}}\left( 30a+24b+21 \right)=2\). Giá trị của a + b bằng?
- A. 7
- B. 6
- C. 20
- D. 11
-
Câu 45: Mã câu hỏi: 473995
Cho một miếng tôn có diện tích \(10000\pi ~\left( c{{m}^{2}} \right)\). Người ta dùng miếng tôn hình tròn để tạo thành hình nón có diện tích toàn phần đúng bằng diện tích miếng tôn. Khi đó khối nón có thể tích lớn nhất được tạo thành sẽ có bán kính hình tròn đáy bằng bao nhiêu?
- A. \(50\sqrt{2}\left( \text{cm} \right).\)
- B. \(50\left( \text{cm} \right). \)
- C. \(20\left( \text{cm} \right). \)
- D. \(25\left( \text{cm} \right).\)
-
Câu 46: Mã câu hỏi: 473999
Cho các số thực dương x, y thỏa mãn \({{2023}^{4{{x}^{2}}-y+7x+10}}-\frac{{{\left( 2x+1 \right)}^{2}}}{y-3x-9}=0\). Tìm giá trị nhỏ nhất của biểu thức M = y - 11x?
- A. 3
- B. 11
- C. 9
- D. -2
-
Câu 47: Mã câu hỏi: 474005
Có bao nhiêu giá trị nguyên của tham số \(m\in \left[ -2023;2023 \right]\) để phương trình \({{4}^{x}}+1=2m+{{\log }_{2}}\left( 4\left( 2x+1 \right)+8m \right)\) có nghiệm?
- A. 2023
- B. 2021
- C. 2020
- D. 2024
-
Câu 48: Mã câu hỏi: 474012
Biết bất phương trình \({{\log }_{2}}\left( {{3}^{x}}-3 \right){{\log }_{8}}\left( {{3}^{x}}{{2}^{-2}}-\frac{3}{4} \right)\le 1\) có tập nghiệm là đoạn \(\left[ a;b \right]\). Giá trị biểu thức a + b bằng?
- A. \(1+{{\log }_{3}}77. \)
- B. \(-2+{{\log }_{2}}\frac{77}{2}. \)
- C. \(-1+{{\log }_{2}}77.\)
- D. \({{\log }_{3}}\frac{77}{2}. \)
-
Câu 49: Mã câu hỏi: 474020
Cho hình lập phương ABCD.A'B'C'D'. Gọi N, P là các điểm lần lượt thuộc các cạnh BC và CD sao cho BN = 3NC và DP = 3PC. Mặt phẳng \(\left( A'NP \right)\) chia khối lập phương thành 2 phần có thể tích là \({{V}_{1}}\) và \({{V}_{2}}\), trong đó \({{V}_{1}}<{{V}_{2}}\). Tính tỷ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\)?
- A. \(\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{289}{472}.\)
- B. \( \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{289}{383}\)
- C. \( \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{25}{47}\).
- D. \(\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{25}{49}.\)
-
Câu 50: Mã câu hỏi: 474024
Cho hình chóp S.ABC có SA vuông góc với đáy, AB = a, \(AC=a\sqrt{2}\), \(\widehat{BAC}=135{}^\circ\). Gọi M, N lần lượt là hình chiếu vuông góc của A trên SB và SC, góc giữa \(\left( AMN \right)\) và \(\left( ABC \right)\) bằng \(30{}^\circ\). Thể tích khối chóp S.ABC bằng?
- A. \(\frac{{{a}^{3}}\sqrt{30}}{3}. \)
- B. \( \frac{{{a}^{3}}\sqrt{30}}{6}. \)
- C. \(\frac{2{{a}^{3}}\sqrt{30}}{9}. \)
- D. \(\frac{{{a}^{3}}\sqrt{21}}{9}.\)





.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)

