Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 464639
Cho biết \(\int\limits_{0}^{1}{f\left( x \right)}dx=\frac{1}{3}\) và \(\int\limits_{0}^{1}{g\left( x \right)}dx=\frac{4}{3}\). Khi đó \(\int\limits_{0}^{1}{\left( g\left( x \right)-f\left( x \right) \right)}dx\) bằng?
- A. \(-\frac{5}{3}\).
- B. \(\frac{5}{3}\).
- C. \(-1\).
- D. \(1\).
-
Câu 2: Mã câu hỏi: 464642
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Góc giữa 2 đường thẳng \(AB\) và \({B}'{D}'\) bằng?
- A. \({{30}^{\text{o}}}\).
- B. \({{135}^{\text{o}}}\).
- C. \({{45}^{\text{o}}}\).
- D. \({{90}^{\text{o}}}\).
-
Câu 3: Mã câu hỏi: 464645
Tìm tập xác định của hàm số \(y=\log x+\log \left( 3-x \right)\)?
- A. \(\left( 3;+\infty \right)\).
- B. \(\left( 0;3 \right)\).
- C. \(\left[ 3;+\infty \right)\).
- D. \(\left( 0;3 \right]\).
-
Câu 4: Mã câu hỏi: 464648
Cho góc ở đỉnh của 1 hình nón bằng \({{60}^{0}}\). Gọi \(r,h,l\) lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
- A. \(l=2r.\)
- B. \(h=2r.\)
- C. \(l=r.\)
- D. \(h=r.\)
-
Câu 5: Mã câu hỏi: 464649
Cho các số phức sau \(z=2+i\) và \(w=3-i.\) Phần thực của số phức \(z+w\) bằng?
- A. \(0\).
- B. \(-1\).
- C. \(5\).
- D. \(1\).
-
Câu 6: Mã câu hỏi: 464652
Trong không gian \(Oxyz\), đường thẳng \(\Delta \) đi qua \(A\left( -1;-1;1 \right)\) và nhận \(\overrightarrow{u}=\left( 1;2;3 \right)\) làm VTCP có phương trình chính tắc là?
- A. \(\frac{x-1}{1}=\frac{y-1}{2}=\frac{z+1}{3}.\)
- B. \(\frac{x+1}{-1}=\frac{y+2}{-1}=\frac{z+3}{1}.\)
- C. \(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z-1}{3}.\)
- D. \(\frac{x-1}{-1}=\frac{y-2}{-1}=\frac{z-3}{1}.\)
-
Câu 7: Mã câu hỏi: 464655
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
.png)
- A. \(\left( 0;1 \right).\)
- B. \(\left( -2;-1 \right).\)
- C. \(\left( -1;0 \right).\)
- D. \(\left( -1;3 \right).\)
-
Câu 8: Mã câu hỏi: 464658
Họ các nguyên hàm của HS \(f(x)=\sin 3x\) là?
- A. \(-\frac{1}{3}\cos 3x+C\).
- B. \(-\cos 3x+C\).
- C. \(\cos 3x+C\).
- D. \(\frac{1}{3}\cos 3x+C\).
-
Câu 9: Mã câu hỏi: 464660
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình:

Hàm số đã cho có bao nhiêu điểm cực trị?
- A. 3
- B. 4
- C. 2
- D. 5
-
Câu 10: Mã câu hỏi: 464662
Cho CSC \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=1\) và \({{u}_{3}}=\frac{1}{3}\). Công sai của \(\left( {{u}_{n}} \right)\) bằng?
- A. \(\frac{2}{3}\).
- B. \(-\frac{1}{3}\).
- C. \(-\frac{2}{3}\).
- D. \(\frac{2}{3}\)
-
Câu 11: Mã câu hỏi: 464667
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình. Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ -3;3 \right]\) bằng?
.png)
- A. 0
- B. 8
- C. 2
- D. 3
-
Câu 12: Mã câu hỏi: 464672
Hãy cho biết nghiệm của phương trình \({{2}^{x-1}}=8\) là?
- A. \(x=3\).
- B. \(x=2\).
- C. \(x=4\).
- D. \(x=5\).
-
Câu 13: Mã câu hỏi: 464675
Tính chu vi đường tròn lớn của mặt cầu \(S\left( O;R \right)\) là?
- A. \(\pi {{R}^{2}}\).
- B. \(4\pi {{R}^{2}}\).
- C. \(\pi R\).
- D. \(2\pi R\).
-
Câu 14: Mã câu hỏi: 464683
Trong không gian \(Oxyz\), vectơ pháp tuyến của mặt phẳng \(\left( Oyz \right)\) là?
- A. \(\overrightarrow{i}\left( 1;0;0 \right)\).
- B. \(\overrightarrow{n}\left( 0;1;1 \right)\).
- C. \(\overrightarrow{j}\left( 0;1;0 \right)\).
- D. \(\overrightarrow{k}\left( 0;0;1 \right)\).
-
Câu 15: Mã câu hỏi: 464687
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình. Hỏi phương trình \(2f\left( x \right)=5\) có bao nhiêu nghiệm trên đoạn \(\left[ -1;2 \right]\)?
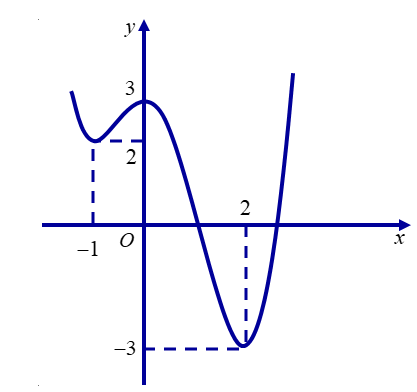
- A. 4
- B. 2
- C. 3
- D. 1
-
Câu 16: Mã câu hỏi: 464693
Đồ thị hàm số \(y=\frac{x+3}{{{x}^{3}}-3x}\) có tất cả bao nhiêu đường tiệm cận?
- A. 3
- B. 4
- C. 2
- D. 1
-
Câu 17: Mã câu hỏi: 464696
Cho khối trụ có đường cao bằng \(2\), chu vi của thiết diện qua trục gấp \(3\) lần đường kính đáy. Thể tích của khối trụ đó bằng?
- A. \(2\pi \).
- B. \(32\pi \).
- C. \(\frac{8\pi }{3}\).
- D. \(8\pi \).
-
Câu 18: Mã câu hỏi: 464699
Gọi \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức của phương trình sau \({{z}^{2}}-3z+5=0\). Môđun của số phức \(\left( 2{{{\bar{z}}}_{1}}-3 \right)\left( 2{{{\bar{z}}}_{2}}-3 \right)\) bằng?
- A. 29
- B. 7
- C. 1
- D. 11
-
Câu 19: Mã câu hỏi: 464702
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị như hình. Phương trình \(f\left( {{x}^{2}} \right)+1=0\) có bao nhiêu nghiệm?
- A. 6
- B. 3
- C. 4
- D. 2
-
Câu 20: Mã câu hỏi: 464705
Đạo hàm của hàm số sau \(f\left( x \right)=\frac{{{2}^{x}}-1}{{{2}^{x}}+1}\) là?
- A. \(\frac{{{2}^{x+1}}\ln 2}{{{\left( {{2}^{x}}+1 \right)}^{2}}}\).
- B. \(\frac{{{2}^{x}}\ln 2}{{{\left( {{2}^{x}}+1 \right)}^{2}}}\).
- C. \(\frac{{{2}^{x+1}}}{{{\left( {{2}^{x}}+1 \right)}^{2}}}\).
- D. \(\frac{{{2}^{x}}}{{{\left( {{2}^{x}}+1 \right)}^{2}}}\).
-
Câu 21: Mã câu hỏi: 464708
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), \(O\) là tâm mặt đáy. Khoảng cách giữa 2 đường thẳng \(SO\) và \(CD\) bằng?
- A. \(\frac{a}{2}\).
- B. \(a\).
- C. \(\frac{a\sqrt{2}}{2}\)
- D. \(a\sqrt{2}\).
-
Câu 22: Mã câu hỏi: 464711
Giả sử \(f\left( x \right)\) là hàm liên tục \(\left( 0;\,+\infty \right)\) và diện tích hình phẳng được kẻ sọc bằng \(3\). Tích phân \(\int\limits_{0}^{1}{f\left( 2x \right)\text{d}x}\) bằng?
- A. \(\frac{4}{3}\).
- B. \(3\).
- C. \(2\)
- D. \(\frac{3}{2}\).
-
Câu 23: Mã câu hỏi: 464718
Trong không gian \(Oxyz\), đường thẳng \(\Delta :\frac{x}{1}=\frac{y-1}{1}=\frac{z}{-1}\) song song với mặt phẳng nào?
- A. \(\left( P \right):x+y-z=0\).
- B. \(\left( \beta \right):x+z=0\).
- C. \(\left( Q \right):x+y+2z=0\).
- D. \(\left( \alpha \right):x-y+1=0\).
-
Câu 24: Mã câu hỏi: 464724
Cho các số thực dương sau \(a\,,\,b\) thỏa mãn \({{\log }_{2}}\left( a+b \right)=3+{{\log }_{2}}ab\). Giá trị \(\frac{1}{a}+\frac{1}{b}\) bằng?
- A. \(3\).
- B. \(\frac{1}{3}\).
- C. \(\frac{1}{8}\).
- D. \(8\).
-
Câu 25: Mã câu hỏi: 464773
Cho biết họ các nguyên hàm của hàm số \(f\left( x \right)={{3}^{2x-1}}\) là?
- A. \(\frac{{{9}^{x}}}{3}+C\).
- B. \(\frac{{{9}^{x}}}{3\ln 3}+C\).
- C. \(\frac{{{9}^{x}}}{6\ln 3}+C\).
- D. \(\frac{{{9}^{x}}}{6}+C\).
-
Câu 26: Mã câu hỏi: 464783
Cho khối lăng trụ tam giác \(ABC.{A}'{B}'{C}'\) có cạnh \(A{A}'=2a\) và tạo với mp đáy 1 góc bằng \(60{}^\circ \), diện tích tam giác \(ABC\) bằng \({{a}^{2}}\). Thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\) bằng?
- A. \(\frac{\sqrt{3}{{a}^{3}}}{3}\).
- B. \({{a}^{3}}\).
- C. \(\sqrt{3}{{a}^{3}}\).
- D. \(\frac{{{a}^{3}}}{3}\).
-
Câu 27: Mã câu hỏi: 464787
Trong không gian \(Oxyz,\) cho đường thẳng \(\Delta \) là giao tuyến của 2 mặt phẳng \(\left( \alpha \right):x+y+z+1=0\) và \(\left( \beta \right):x+2y+3z+4=0.\) Một vectơ chỉ phương của \(\Delta \) có tọa độ là?
- A. \(\left( 2;-1;-1 \right).\)
- B. \(\left( 1;-1;0 \right).\)
- C. \(\left( 1;1;-1 \right).\)
- D. \(\left( 1;-2;1 \right).\)
-
Câu 28: Mã câu hỏi: 464790
Cho một tổ học sinh có 12 bạn, gồm 7 nam và 5 nữ. Cần chọn một nhóm 3 học sinh của tổ đó để làm vệ sinh lớp học. Hỏi có bao nhiêu cách chọn sao cho trong nhóm có cả nam và nữ?
- A. \(22.\)
- B. \(175.\)
- C. \(43.\)
- D. \(350.\)
-
Câu 29: Mã câu hỏi: 464793
Giả sử hàm số \(f\left( x \right)\) có đạo hàm liên tục trên. Biết rằng \(G\left( x \right)={{x}^{3}}\) là 1 nguyên hàm của \(g\left( x \right)={{e}^{-2x}}f\left( x \right)\) trên \(\mathbb{R}\). Họ tất cả các nguyên hàm của \({{e}^{-2x}}{f}'\left( x \right)\) là?
- A. \(-2{{x}^{3}}+3{{x}^{2}}+C\).
- B. \(2{{x}^{3}}+3{{x}^{2}}+C\).
- C. \({{x}^{3}}+3{{x}^{2}}+C\).
- D. \(-{{x}^{3}}+3{{x}^{2}}+C\).
-
Câu 30: Mã câu hỏi: 464797
Có tất cả bao nhiêu số nguyên \(m\) để hàm số \(f\left( x \right)=3x+m\sqrt{{{x}^{2}}+1}\) đồng biến trên \(\mathbb{R}\)?
- A. 5
- B. 1
- C. 7
- D. 2
-
Câu 31: Mã câu hỏi: 464799
Hàm số \(f\left( x \right)={{x}^{4}}{{\left( x-1 \right)}^{2}}\) có tất cả bao nhiêu điểm cực trị?
- A. 3
- B. 0
- C. 5
- D. 1
-
Câu 32: Mã câu hỏi: 464802
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Có mặt bên \(SAB\) là tam giác đều cạnh \(\sqrt{3}a\), \(ABC\) là tam giác vuông tại \(A\) có cạnh \(AC=a\), góc giữa \(AD\) và \((SAB)\) bằng \(30{}^\circ \). Thể tích khối chóp \(S.ABCD\) bằng?
- A. \({{a}^{3}}\).
- B. \(\frac{\sqrt{3}{{a}^{3}}}{6}\).
- C. \(\frac{\sqrt{3}{{a}^{3}}}{2}\).
- D. \(\frac{\sqrt{3}{{a}^{3}}}{4}\).
-
Câu 33: Mã câu hỏi: 464808
Có tất cả bao nhiêu số phức \(z\) đôi một khác nhau thỏa mãn \(\left| z+i \right|=2\) và \({{\left( z-2 \right)}^{4}}\) là số thực?
- A. 4
- B. 5
- C. 6
- D. 8
-
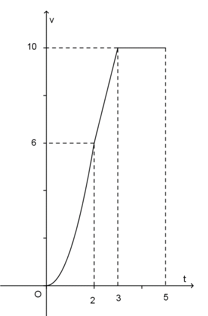
Câu 34: Mã câu hỏi: 464814
Một chiếc xe đua \({{F}_{1}}\) đạt tới vận tốc lớn nhất là \(360\,km/h\). Đồ thị dưới biểu thị vận tốc \(v\) của xe trong \(5\) giây đầu tiên kể từ lúc xuất phát. Đồ thị trong \(2\) giây đầu tiên là một phần của parabol đỉnh tại gốc tọa độ \(O\), giây tiếp theo là đoạn thẳng và sau đúng \(3\) giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị \(1\) giây, mỗi đơn vị trục tung biểu thị \(10\,m/s\) và trong \(5\) giây đầu xe chuyển động theo đường thẳng. Hỏi trong \(5\) giây đó xe đã đi được quãng đường là bao nhiêu?
- A. \(340\) (mét).
- B. \(420\) (mét).
- C. \(400\) (mét).
- D. \(320\) (mét).
-
Câu 35: Mã câu hỏi: 464819
Cho \(10\) học sinh gồm \(5\) bạn lớp \(12A\) và \(5\) bạn lớp \(12B\) tham gia một trò chơi. Để thực hiện trò chơi, người điều khiển ghép ngẫu nhiên \(10\) học sinh đó thành \(5\) cặp. Xác suất để không có cặp nào gồm hai học sinh cùng lớp bằng?
- A. \(\frac{4}{63}\).
- B. \(\frac{1}{63}\).
- C. \(\frac{2}{63}\).
- D. \(\frac{8}{63}\).
-
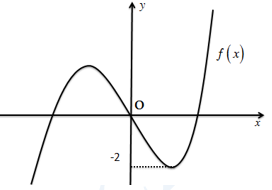
Câu 36: Mã câu hỏi: 464821
Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) (với \(a,b,c,d\in \mathbb{R}\)) có đồ thị như hình:
Có bao nhiêu số dương trong các số \(a,b,c,d\)?
- A. 0
- B. 1
- C. 2
- D. 4
-
Câu 37: Mã câu hỏi: 464824
Trong không gian \(Oxyz\), cho mp \(\left( \alpha \right)\) vuông góc với \(\Delta :\frac{x}{1}=\frac{y}{-2}=\frac{z}{3}\) và \(\left( \alpha \right)\) cắt trục \(Ox\), trục \(Oy\) và tia \(Oz\) lần lượt tại \(M\), \(N\), \(P\). Biết rằng thể tích khối tứ diện \(OMNP\) bằng \(6\). Mặt phẳng \(\left( \alpha \right)\) đi qua điểm nào sau đây?
- A. \(B\left( 1;-1;1 \right)\).
- B. \(A\left( 1;-1;-3 \right)\).
- C. \(C\left( 1;-1;2 \right)\).
- D. \(D\left( 1;-1;-2 \right)\).\(D\left( 1;-1;-2 \right)\).
-
Câu 38: Mã câu hỏi: 464826
Cho đồ thị \(\left( C \right):y=\frac{x}{x-1}\). Đường thẳng \(d\) đi qua điểm \(I\left( 1;1 \right)\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(A\) và \(B\). Khi diện tích tam giác \(MAB\) đạt giá trị nhỏ nhất, với \(M\left( 0;3 \right)\) thì độ dài đoạn \(AB\) bằng?
- A. \(\sqrt{10}\).
- B. \(\sqrt{6}\).
- C. \(2\sqrt{2}\).
- D. \(2\sqrt{3}\).
-
Câu 39: Mã câu hỏi: 464838
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân, \(AB=BC=2a\). Tam giác \(SAC\) cân tại \(S\) và nằm trong mp vuông góc \(\left( ABC \right)\), \(SA=a\sqrt{3}\). Góc giữa 2 mặt phẳng \(\left( SAB \right)\) và \(\left( SAC \right)\) bằng?
- A. \(60{}^\circ \).
- B. \(30{}^\circ \).
- C. \(45{}^\circ \).
- D. \(90{}^\circ \).
-
Câu 40: Mã câu hỏi: 464839
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có \(AB=A{A}'=2a\), \(AC=a\), \(\widehat{BAC}=120{}^\circ \). Tính bán kính mặt cầu ngoại tiếp hình chóp \(A.BC{C}'{B}'\)?
- A. \(\frac{\sqrt{10}a}{3}\).
- B. \(\frac{\sqrt{30}a}{3}\).
- C. \(\frac{\sqrt{30}a}{10}\).
- D. \(\frac{\sqrt{33}a}{3}\).
-
Câu 41: Mã câu hỏi: 464841
Cho HS \(f\left( x \right)\) nhận giá trị dương và có đạo hàm liên tục trên \(\left[ 1;\ e \right]\). Biết \(f\left( 1 \right)=1\) và \(x.f\left( x \right).{f}'\left( x \right)={{x}^{2}}+{{f}^{2}}\left( x \right)\) với mọi \(x\in \left[ 1;\ e \right].\) Khi đó, \(\int\limits_{1}^{e}{\frac{f\left( x \right)}{{{x}^{2}}}dx}\) bằng?
- A. \(\frac{2}{3}\).
- B. \(\frac{3\sqrt{3}-1}{3}\).
- C. \(\frac{\sqrt{3}-1}{3}\).
- D. \(\sqrt{3}\).
-
Câu 42: Mã câu hỏi: 464842
Trong không gian \(Oxyz\), cho mp \(\left( P \right):ax+by+cz+7=0\) qua điểm \(A\left( 2;0;1 \right)\), vuông góc với mặt phẳng \(\left( Q \right):3x-y+z+1=0\) và tạo với mặt phẳng \(\left( R \right):x-y+2z-1=0\) một góc \({{60}^{\text{o}}}\). Tổng \(a+b+c\) bằng?
- A. 19
- B. 0
- C. -14
- D. 5
-
Câu 43: Mã câu hỏi: 464843
Xét các số phức \(z=a+bi,\,\,\left( a,\,\,b\in \mathbb{R} \right)\) thỏa mãn \(\left| z-2+3i \right|=4\) và \(\left| z+1-4i \right|+\left| z-9 \right|\) đạt GTLN. Khi đó \(5a-2b\) bằng?
- A. 4
- B. 8
- C. 16
- D. 5
-
Câu 44: Mã câu hỏi: 464845
Biết khoảng (a; b) là tập hợp tất cả các giá trị dương của tham số m để pt \(3{{\log }_{27}}\left( 2{{\text{x}}^{2}}-x+2m-4{{m}^{2}} \right)+{{\log }_{\frac{1}{\sqrt{3}}}}\sqrt{{{x}^{2}}+mx-2{{m}^{2}}}=0\left( 1 \right)\) có 2 nghiệm \({{x}_{1}},{{x}_{2}}\)thỏa mãn \(x_{1}^{2}+x_{2}^{2}>1\). Tính K = 5a + 2b?
- A. \(K=\frac{1}{2}\).
- B. \(K=\frac{5}{2}\).
- C. \(K=3\).
- D. \(K=2\).
-
Câu 45: Mã câu hỏi: 464849
Cho hàm số \(f\left( x \right)\) là hàm số đa thức bậc bốn. Biết \(f\left( 0 \right)=0\) và ĐTHS \(y={f}'\left( x \right)\) có hình vẽ:
Tập nghiệm của phương trình \(f\left( \left| 2\sin x-1 \right|-1 \right)=m\) (với \(m\) là tham số) trên đoạn \(\left[ 0;3\pi\right]\) có tất cả bao nhiêu phần tử?
- A. 8
- B. 23
- C. 12
- D. 16
-
Câu 46: Mã câu hỏi: 464856
Giả sử \(f\left( x \right)\) là hàm có đạo hàm liên tục trên khoảng \(\left( 0;\pi \right)\) và \(f'\left( x \right)\sin x=x+f\left( x \right)\cos x,\,\,\,\forall x\in \left( 0;\pi \right).\) Biết \(f\left( \frac{\pi }{2} \right)=1,\,\,f\left( \frac{\pi }{6} \right)=\frac{1}{12}\left( a+b\ln 2+c\pi \sqrt{3} \right)\), với \(a,\,\,b,\,\,c\) là các số nguyên. Giá trị \(a+b+c\) bằng?
- A. -1
- B. 1
- C. 11
- D. 12
-
Câu 47: Mã câu hỏi: 464861
Xét tất cả các số thực dương \(x;y\) thỏa \(\frac{x+y}{10}+\log \left( \frac{1}{2x}+\frac{1}{2y} \right)=1+2xy\). Khi biểu thức \(\frac{4}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}\) đạt giá trị nhỏ nhất, tích \(xy\) bằng?
- A. \(\frac{9}{100}\).
- B. \(\frac{9}{200}\).
- C. \(\frac{1}{64}\).
- D. \(\frac{1}{32}\).
-
Câu 48: Mã câu hỏi: 464867
Cho khối chóp \({S.ABCD}\) có đáy \({ABCD}\) là hình thoi, \({\widehat{DAB}=60{}^\circ }\), \({AD=a}\), tam giác \({SBC}\) cân tại \({S}\), tam giác \({SCD}\) vuông tại \({C}\), k/c giữa \({SA}\) và \({CD}\) bằng \({\frac{4a}{5}}\). Thể tích của khối chóp đã cho bằng?
- A. \(\frac{2{{a}^{3}}}{\sqrt{11}}\).
- B. \(\frac{4{{a}^{3}}}{\sqrt{11}}\).
- C. \(\frac{4{{a}^{3}}}{3\sqrt{11}}\).
- D. \(\frac{2{{a}^{3}}}{3\sqrt{11}}\).
-
Câu 49: Mã câu hỏi: 464868
Có tất cả bao nhiêu số nguyên \(a\) để phương trình \({{z}^{2}}-\left( a-3 \right)z+{{a}^{2}}+a=0\) có hai nghiệm phức \({{z}_{1}}\), \({{z}_{2}}\)thỏa mãn \(\left| {{z}_{1}}+{{z}_{2}} \right|=\left| {{z}_{1}}-{{z}_{2}} \right|\)?
- A. 4
- B. 2
- C. 3
- D. 1
-
Câu 50: Mã câu hỏi: 464875
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{{x}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+3 \right)}^{2}}=24\) cắt mp \(\left( \alpha \right):x+y=0\) theo giao tuyến là đường tròn \(\left( C \right)\). Tìm hoành độ của điểm \(M\) thuộc đường tròn \(\left( C \right)\) sao cho k/c từ \(M\) đến \(A\left( 6;-10;3 \right)\) lớn nhất?
- A. -1
- B. -4
- C. 2
- D. 4





.PNG)
.PNG)
.PNG)

