Câu hỏi trắc nghiệm (30 câu):
-
Câu 1: Mã câu hỏi: 166980
Đồ thị sau đây là của hàm số nào?
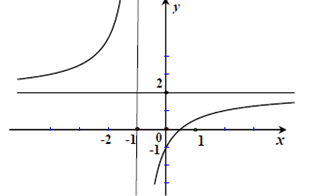
- A. \(y = \dfrac{{1 - 2x}}{{x - 1}}\)
- B. \(y = \dfrac{{2x + 1}}{{x + 1}}\)
- C. \(y = \dfrac{{2x + 1}}{{x - 1}}\)
- D. \(y = \dfrac{{2x - 1}}{{x + 1}}\)
-
Câu 2: Mã câu hỏi: 166988
Đồ tị hàm số \(y = {x^3} - 3{x^2} + 1\) cắt đường thẳng y = m tại ba điểm phân biệt thì tất cả các giá trị tham số m thỏa mãn là giá trj nào?
- A. \(m > 1\)
- B. \( - 3 \le m \le 1\)
- C. \(-3 < m < 1\)
- D. \(m < - 3\)
-
Câu 3: Mã câu hỏi: 166995
Đường thẳng y = x – 1 cắt đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\) tại các điểm có tọa độ là bao nhiêu?
- A. (0 ; - 1), (2 ; 1)
- B. (0 ; 2)
- C. (1 ; 2)
- D. (- 1 ; 0), (2 ; 1)
-
Câu 4: Mã câu hỏi: 167003
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số \(y = \dfrac{{{x^3}}}{ 3} - 2{x^2} + 3x - 5\).
- A. Song song với trục tung
- B. Có hệ số góc dương
- C. Có hệ số góc âm
- D. Song song với trục hoành.
-
Câu 5: Mã câu hỏi: 167012
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{1 - 4x} }{ {2x - 1}}\).
- A. \(y = 2\)
- B. \(y = 4\)
- C. \(\frac{1}{2}\)
- D. \(y = - 2 \)
-
Câu 6: Mã câu hỏi: 167016
Đường cong trong hình dưới đây là đồ thị của hàm số nào ?
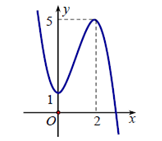
- A. \(y = - {x^3} + 2{x^2} - 1\)
- B. \(y = {x^3} - 3{x^2} + 1\)
- C. \(y = - {x^3} + 3{x^2} + 1\)
- D. \(y = - {x^3} + 3{x^2} - 4\)
-
Câu 7: Mã câu hỏi: 167021
Cho hàm số y = f(x) có bảng biến thiên như sau.
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
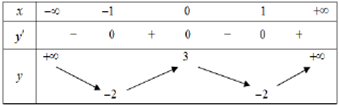
- A. \((0 ; 1)\)
- B. \(( - \infty ;0)\)
- C. \((1; + \infty )\)
- D. \((- 1 ; 0)\)
-
Câu 8: Mã câu hỏi: 167028
Tìm tất cả các giá trị của m để dồ thị hàm số \(y = {x^3} - 3x + 2\) cắt đường thẳng y = m – 1 tại ba điểm phân biệt.
- A. \(0 < m < 4\)
- B. \(1 < m \le 5\)
- C. \(1 < m < 5\)
- D. \(1 \le m < 5\)
-
Câu 9: Mã câu hỏi: 167032
Đồ thị hàm số nào sau đây có tâm đối xứng là điểm I(1 ; -2 )?
- A. \(y = \dfrac{{2x - 3} }{ {2x + 4}}\)
- B. \(y = 2{x^3} - 6{x^2} + x + 1\)
- C. \(y = - 2{x^3} + 6{x^2} + x - 1\)
- D. \(y =\dfrac {{2 - 2x} }{{1 - x}}\)
-
Câu 10: Mã câu hỏi: 167035
Cho hàm số y = f(x) có bảng biến thiên cho bởi bảng sau:
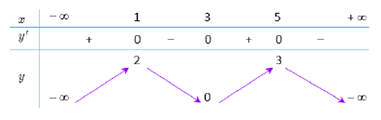
Kết luận nào sau đây sai?
- A. Giá trị cực tiểu của hàm số bằng 3
- B. f(x) đồng biến trên mỗi khoảng \(( - \infty ;1),\,(3;5)\)
- C. Điểm cực đại của đồ thị hàm số là (1 ; 2), (5 ; 3)
- D. f(x) nghịch biến trên môĩ khoảng \((1;3),\,(5; + \infty )\)
-
Câu 11: Mã câu hỏi: 167043
Cho hàm số \(f(x) = 2x + m + {\log _2}[m{x^2} - 2(m - 2)x + 2m - 1]\) ( m là tham số). Tìm tất cả các giá trị của m để hàm số f(x) xác định với mọi \(x \in R\).
- A. \(m > 0\)
- B. \(m > 1\)
- C. \(m > 1 \cup m < - 4\)
- D. \(m < - 4\)
-
Câu 12: Mã câu hỏi: 167045
Tìm số nghiệm của phương trình \({\log _3}({x^3} - 3x) = \dfrac{1}{2}\)
- A. 2
- B. 3
- C. 0
- D. 1
-
Câu 13: Mã câu hỏi: 167050
Giá trị của \({4^{{1 \over 2}{{\log }_2}3 + 3{{\log }_8}5}}\) bằng bao nhiêu?
- A. 25
- B. 50
- C. 75
- D. 45
-
Câu 14: Mã câu hỏi: 167055
Tính đạo hàm của hàm số \(y = {2^{2x + 3}}\)
- A. \({2^{2x + 3}}.\ln 2\)
- B. \((2x + 3){2^{2x + 2}}.\ln 2\)
- C. \({2.2^{2x + 3}}\)
- D. \({2.2^{2x + 3}}.\ln 2\)
-
Câu 15: Mã câu hỏi: 167065
Nếu \({\log _7}x = 8{\log _7}a{b^2} - 2{\log _7}{a^3}b\,\,(a,b > 0)\) thì x bằng mấy?
- A. \({a^4}{b^6}\)
- B. \({a^6}{b^{12}}\)
- C. \({a^2}{b^{14}}\)
- D. \({a^8}{b^{14}}\)
-
Câu 16: Mã câu hỏi: 167071
Tính \(K = {\left( {{1 \over {16}}} \right)^{ - 0,75}} + {\left( {{1 \over 8}} \right)^{ - {4 \over 3}}}\), ta được:
- A. 12
- B. 24
- C. 18
- D. 16
-
Câu 17: Mã câu hỏi: 167077
Nếu \({1 \over 2}\left( {{a^\alpha } + {a^{ - \alpha }}} \right) = 1\) thì giá trị của \(\alpha\) bằng bao nhiêu?
- A. 3
- B. 2
- C. 1
- D. 0
-
Câu 18: Mã câu hỏi: 167087
Gọi x1, x2 là hai nghiệm của phương trình \({4^x} - {8.2^x} + 4 = 0\). Tính giá trị của biểu thức P=x1 + x2.
- A. - 4
- B. 4
- C. 0
- D. 2
-
Câu 19: Mã câu hỏi: 167091
Tìm điều kiện xác định của bất phương trình \({\log _{0,4}}(x - 4) \ge 0\).
- A. \(\left( {4;{{13} \over 2}} \right]\)
- B. \((4; + \infty )\)
- C. \(\left[ {{{13} \over 2}; + \infty } \right)\)
- D. \(\left( { - \infty ;{{13} \over 2}} \right)\)
-
Câu 20: Mã câu hỏi: 167096
Tìm nghiệm của phương trình \({3^x} + {3^{x + 1}} = 8\).
- A. \(x = 1\)
- B. \(x = 2\)
- C. \(x = {\log _2}3\)
- D. \(x = {\log _3}2\)
-
Câu 21: Mã câu hỏi: 167102
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
- A. \(V = Sh\)
- B. \(V = \dfrac{1}{2}Sh\)
- C. \(V = \dfrac{1}{3}Sh\)
- D. \(V = \dfrac{1}{6}Sh\)
-
Câu 22: Mã câu hỏi: 167146
Một khối chóp có đáy là đa giác n cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng?
- A. Số mặt và số đỉnh bằng nhau
- B. Số đỉnh của khối chóp bằng n
- C. Số cạnh của khối chóp bằng n + 1
- D. Số mặt của khối chóp bằng 2n
-
Câu 23: Mã câu hỏi: 167154
Cho khối chóp tam giác S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A', B', C'. Khi đó:
- A. \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}} + \dfrac{{SB'}}{{SB}} + \dfrac{{SC'}}{{SC}}\)
- B. \(\dfrac{{{V_{S.ABC}}}}{{{V_{S.A'B'C'}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)
- C. \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}} = \dfrac{{SB'}}{{SB}} = \dfrac{{SC'}}{{SC}}\)
- D. \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)
-
Câu 24: Mã câu hỏi: 167162
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
- A. \(\dfrac{{{a^3}}}{6}\)
- B. \(\dfrac{{{a^3}}}{3}\)
- C. \(\dfrac{{{a^3}}}{4}\)
- D. \(\dfrac{{{a^3}}}{8}\)
-
Câu 25: Mã câu hỏi: 167167
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?
- A. Năm mặt
- B. Hai mặt
- C. Ba mặt
- D. Bốn mặt
-
Câu 26: Mã câu hỏi: 167181
Với điểm O cố định thuộc mặt phẳng (P) cho trước, xét đường thẳng l thay đổi đi qua điểm O và tạo với mặt phẳng (P) một góc \({30^o}\). Tập hợp các đường thẳng trong không gian là
- A. Một mặt phẳng
- B. Hai đường thẳng
- C. Một mặt trụ
- D. Một mặt nón
-
Câu 27: Mã câu hỏi: 167189
Diện tích xung quanh của một hình nón tròn xoay nội tiếp tứ diện đều cạnh a là
- A. \({S_{xq}} = \dfrac{{\pi {a^2}}}{4}\)
- B. \({S_{xq}} = \dfrac{{\pi \sqrt 2 {a^2}}}{6}\)
- C. \({S_{xq}} = \dfrac{{\pi \sqrt 3 {a^2}}}{6}\)
- D. \({S_{xq}} = \dfrac{{2\pi {a^2}}}{3}\)
-
Câu 28: Mã câu hỏi: 167195
Diện tích xung quanh của một hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a là
- A. \({S_{xq}} = \dfrac{{\pi {a^2}}}{3}\)
- B. \({S_{xq}} = \dfrac{{\pi \sqrt 2 {a^2}}}{3}\)
- C. \({S_{xq}} = \dfrac{{\pi \sqrt 3 {a^2}}}{3}\)
- D. \({S_{xq}} = \dfrac{{\pi \sqrt 3 {a^2}}}{6}\)
-
Câu 29: Mã câu hỏi: 167204
Cho hình nón tròn xoay đỉnh S, đáy là đường tròn tâm O, bán kính đáy r = 5. Một thiết diện qua đỉnh là tam giác SAB đều có cạnh bằng 8. Khoảng cách từ O đến mặt phẳng \(\left( {SAB} \right)\) bằng
- A. \(\dfrac{{4\sqrt {13} }}{3}\)
- B. \(\dfrac{{3\sqrt {13} }}{4}\)
- C. \(3\)
- D. \(\dfrac{{\sqrt {13} }}{3}\)
-
Câu 30: Mã câu hỏi: 167213
Cho hai điểm A, B cố định. Tập hợp các điểm M trong không gian sao cho diện tích tam giác MAB không đổi là
- A. Mặt nón tròn xoay
- B. Mặt trụ tròn xoay
- C. Mặt cầu
- D. Hai đường thẳng song song






