Câu 1: Một chất điểm dao  động dọc theo trục Ox. Phương trình dao động là: \(x = 8\cos(2 \pi t - \pi )\) cm. Sau t = 0,5s, kể từ t = 0, quãng đường S vật đã đi là
A. 8 cm                       B. 12 cm                     C. 16 cm                     D. 20 cm

Lời giải:
\(x = 8 \cos (2 \pi t - \pi) \ cm\)
+ Chu kì \(T = \frac{2\pi}{2 \pi} = 1s\)
+ \(\frac{\Delta t }{T} = 0,5 \Rightarrow \Delta t = 0,5 T \Rightarrow S = 2A = 16 \ cm\)
⇒ Chọn C

Câu 2: Vật dao động điều hòa với biên độ A: Thời gian ngắn nhất vật đi từ vị trí cân bằng đến li độ \(x = 0,5\sqrt{3}\) A là 0,2 s. Chu kì dao động của vật là
A. 0,2 s                       B. 0,6 s                       C. 1,2 s                       D. 2,4 s

Lời giải:
Từ x = 0 đến \(x = \frac{A\sqrt{3}}{2} \Rightarrow \Delta t_{min} = \frac{T}{6} = 0,2\)
⇒ T = 1,2s
⇒ Chọn C

Câu 3: Một vật m = 1 kg dao động điều hòa dưới tác dụng của lực \(F = -5\cos10t\) (N). Vận tốc của vật khi qua vị trí cân bằng là
A. 40 cm/s                 B. 50 cm/s                 C. 100 cm/s               D. 12,5 cm/s

Lời giải:
\(m = 1kg; F = -5\cos 10t \ (N)\)
+ Ta có: \(F = -m\omega ^2 = -m\omega ^2 A\có (\omega t + \varphi )\)
\(\Rightarrow m\omega ^2 = 5 \Rightarrow 1.10^2A = 5 \Rightarrow A = 0,05 = 5\ cm\)
+ \(v_{max} = \omega A = 10.5 = 50 \ cm/s\)
⇒ Chọn B

Câu 4: Vật dao động điều hòa thực hiện 10 dao động trong 5 giây. Truyền cho vật nặng vận tốc v = 62,8 cm/s khi vật đang ở vị trí cân bằng  để vật dao động điều hòa. Chọn gốc thời gian lúc vật qua vị trí có li độ \(x = -2,5 \sqrt{2}\) cm cùng chiều (+). Phương trình dao động điều hòa của vật là
A. \(x = 5cos(4 \pi t - \frac{\pi}{4})\ cm\)                             B. \(x = 5cos(4 \pi t + \frac{5 \pi}{4}) \ cm\)                        
C. \(x = 4cos(4 \pi t + \frac{5\pi}{4}) \ cm\)                            D. \(x = 4cos(2 \pi t - \frac{\pi}{4})\ cm\)

Lời giải:
+ \(T = \frac{\Delta t}{n} = \frac{S}{10} = 0,5 \Rightarrow \omega = \frac{2\pi}{T} = 4\pi \frac{rad}{s}\)
+ Vị trí cân bằng: \(v_{max} = 62,8 \frac{cm}{s} = \omega A \Rightarrow A = \frac{v_{max}}{\omega } = 5 \ cm\)
+ \(t = 0: \left\{\begin{matrix} x = -2,5\sqrt{2} \cm\\ v>0 \end{matrix}\right.\) \(\Rightarrow \left\{\begin{matrix} \cos \varphi = - \frac{\sqrt{2}}{2}\\ \sin \varphi < 0 \ \ \ \ \end{matrix}\right. \Rightarrow \varphi = -\frac{3\pi}{4}\)
\(\Rightarrow x= 5\có(4\pi t - \frac{\pi}{3}) = 5\cos (4\pi + \frac{5\pi}{4})\ (cm)\)
⇒ Chọn B

Câu 5: Vật dao động điều hoà theo phương trình: \(x = 6cos(2 \pi t - \frac{2 \pi}{3})\) cm. Vật đi qua vị trí cân bằng lần đầu tiên vào thời điểm
A. \(\frac{1}{12}\) s theo chiều dương của quỹ đạo.       B. \(\frac{1}{6}\) s theo chiều âm của quỹ đạo.
C. \(\frac{1}{12}\) s theo chiều âm của quỹ đạo.             D. \(\frac{1}{6}\) s theo chiều dương của quỹ đạo.

Lời giải:
\(x = 6\cos (2 \pi t - \frac{2 \pi }{3}) \ (cm)\)
\(t = 0: \left\{\begin{matrix} x = -3\ cm\\ v > 0 \ \ \ \ \ \ \ \end{matrix}\right.\)

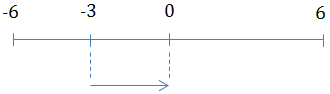
\(\left\{\begin{matrix} \Delta t = \frac{T}{2} = \frac{1}{12}s\\ v > 0 \hspace {1,5cm} \end{matrix}\right.\)
⇒ Chọn A

Câu 6: Vận tốc của một chất điểm dao động điều hoà khi qua vị trí cân bằng là 20\(\pi\) cm/s. Tốc độ trung bình của chất điểm trong một chu kỳ bằng
A. 40 cm/s                 B. 30 cm/s                 C. 20\(\pi\) cm/s             D. 0

Lời giải:
+ \(v_{max} = 20\pi \frac{cm}{s}\)
+ Tốc độ trung bình trong 1 chu kỳ: \(\overline{v} = \frac{4A}{T} = \frac{2}{\pi}v_{max}\)
\(\Rightarrow \overline{v} = \frac{2}{\pi} .20 \pi = 40 \frac{cm}{s}\)
⇒ Chọn A

Câu 7: Một chất điểm dao động với phương trình x = 5cos10t (cm). Khi chất điểm có vận tốc v = 30 cm/s và đang đi về vị trí cân bằng thì nó ở vị trí có li độ
A. x = 4 cm.                B. x = - 4 cm              C. x = - 3 cm              D. x = 3 cm.

Lời giải:
+ x = 5cos10t (cm)
+ Khi \(v = 30\frac{cm}{s} \Rightarrow x = \pm \sqrt{A^2 - \frac{v^2}{\omega ^2}} = \pm \sqrt{5^2 - 3^2} = \pm 4 \ cm\)
+ Vật đang đi về vị trí cân bằng ⇒ v.a > 0 ⇒ a > 0 ⇒ x = -4 cm
⇒ Chọn B

Câu 8: Chất điểm có khối lượng m₁ = 50 gam dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động \(x_1 = \sin(5 \pi t + \frac{\pi}{6})\) (cm). Chất điểm có khối lượng m₂ = 100 gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động \(x_2 = 5\sin(\pi t - \frac{\pi}{6})\) (cm). Tỉ số cơ năng trong quá trình dao động điều hòa của chất điểm m₁ so với chất điểm m₂ bằng
A. 0,5                          B. 2                             C. 1                             D. 0,2

Lời giải:
+ \(m_1 = 50g; x_1 = \sin (5\pi t + \frac{\pi}{6}) \ (cm)\)
+ \(m_2 = 100g; x_2 = 5 \sin (\pi t - \frac{\pi}{6}) \ (cm)\)
Ta có: \(\frac{W_1}{W_2} = \frac{\frac{1}{2}m_1\omega _{1}^{2}A_{1}^{2}}{\frac{1}{2}m_2\omega _{2}^{2}A_{2}^{2}} = \frac{1}{2}\)
⇒ Chọn A

Câu 9: Một vật dao động điều hòa với biên độ 10 cm và tần số 4 Hz. Biết t = 0 lúc vật qua vị trí cân bằng theo chiều dương. Li độ của vật tại thời điểm t = 1,25 s là
A. – 5 cm                    B. 10 cm                     C. 5 cm                       D. 0 cm

Lời giải:
\(A = 10 \ cm; f = 4Hz; t = 0 \left\{\begin{matrix} x = 0\\ v > 0 \end{matrix}\right.\)
\(\Rightarrow x = 10\cos(8\pi t - \frac{\pi}{2}) \ (cm)\)
\(t = 1,25s \Rightarrow x = 10\cos (8 \pi . 1,25 - \frac{\pi}{2}) = 0\)
⇒ Chọn D

Câu 10: Một vật dao động điều hòa theo phương trình \(x = \cos(40t - \frac{\pi}{2})\) (cm). Khi vật có vận tốc 20 cm/s thì nó có
A. thế năng bằng 4 lần động năng.           B. thế năng bằng 8 lần động năng.
C. thế năng bằng 3 lần động năng.           D. thế năng bằng 2 lần động năng.

Lời giải:
\(x = \cos (40t - \frac{\pi}{2}) \ 9cm \Rightarrow v_{max} = A\omega = 40 \frac{cm}{s}\)
\(v = 20 \frac{cm}{s} \Rightarrow\)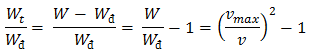  

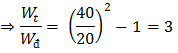
⇒ Chọn C

Câu 11: Một vật dao động điều hòa với tần số góc 4 rad/s. Lúc t = 0, vật đi qua li độ \(x = -5\sqrt{3}\) cm với vận tốc v = -20 cm/s. Viết phương trình dao động
A. \(x = 10\cos(4t + \frac{2\pi}{3}) \ cm\)                          B. \(x = 10\cos(4t + \frac{5 \pi}{6}) \ cm\)
C. \(x = 10\cos(4t + \frac{\pi}{3}) \ cm\)                             D. \(x = 5\sqrt{3} \cos(4t + \frac{\pi}{3})\ cm\)

Lời giải:
\(\omega = 4 \frac{rad}{s}\)
\(t = 0: \left\{\begin{matrix} x = -5\sqrt{3}\ cm\\ v = -20\ cm/s \end{matrix}\right.\)
\(\Rightarrow A = \sqrt{x^2 + \frac{v^2}{\omega ^2}} = \sqrt{(-5\sqrt{3})^2 + \left ( \frac{-20}{4} \right )^2} = 10\ cm\)
\(t = 0: \left\{\begin{matrix} x =-5\sqrt{3}\\ v<0 \ \ \ \ \ \ \end{matrix}\right. \Rightarrow \left\{\begin{matrix} \cos \varphi = -\frac{\sqrt{3}}{2}\\ \sin \varphi > 0 \ \ \ \ \end{matrix}\right. \Rightarrow \varphi = \frac{5\pi}{6}\)
\(\Rightarrow x = 10\cos (4t + \frac{5\pi}{6})\)
⇒ Chọn B

Câu 12: Một vật dao động điều hòa với phương trình \(x = 5\cos(5\pi t + \frac{\pi}{2})\) cm. Sau bao lâu kể từ lúc t = 0, vật đi được quãng đường là 42,5 cm?
A. \(\frac{5}{6}s\)                          B. \(\frac{13}{15}s\)                         C. \(\frac{2}{5}s\)                          D. \(\frac{17}{5}s\)

Lời giải:
\(x = 5\cos (5\pi t + \frac{\pi}{2}) \ (cm)\)
\(S = 42,5 \ cm \Rightarrow \frac{S}{4A} = \frac{42,5}{4.5} = 2 + \frac{1}{2}\)
⇒ S = 2.4A + 2,5 cm
Tại \(t = 0: \left\{\begin{matrix} x = 0\\ v < 0 \end{matrix}\right.\)

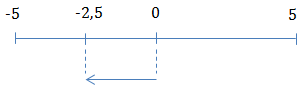
                  \(\Delta t_0 = \frac{T}{2} = \frac{2}{5}.\frac{1}{12} = \frac{1}{30}s\)
\(\Rightarrow \Delta t = 2.T + \Delta t_0 = 2.\frac{2}{5}+\frac{1}{30} = \frac{5}{6}s\)
⇒ Chọn A

Câu 13: Một vật dao động điều hòa theo phương trình \(x = A\cos(2\pi t + \frac{\pi}{3})\) (cm). Vào thời điểm nào sau đây kể từ t = 0, tốc độ của vật đạt cực đại?
A. \(\frac{1}{3}s\)                         B. \(\frac{2}{3}s\)                         C. \(\frac{13}{12}s\)                        D. \(\frac{1}{6}s\)

Lời giải:
\(x = A\cos(2\pi t + \frac{\pi}{3}) \ (cm)\)
\(t = 0: \left\{\begin{matrix} x = \frac{A}{2}\\ v<0 \end{matrix}\right.\)
Tốc độ cực đại khi vật qua trị trí cân bằng

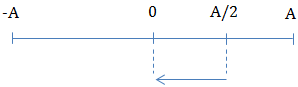
                                   \(\Delta t_1 = \frac{T}{2} = \frac{1}{12}s\)
\(\Rightarrow t_K = st_1 + \frac{KT}{12} = \frac{1}{12} + \frac{K}{2}\)
\(\Rightarrow t_2 = \frac{13}{12}s\)
⇒ Chọn C

Câu 14: Một vật có khối lượng 100 g dao động điều hòa theo phương trình \(x = 5\cos(\omega t + \frac{\pi}{3})\) (cm). Tại thời điểm t = 0 lực kéo về tác dụng vào vật có độ lớn bằng 1 N. Tần số góc có giá trị là
A. 20 rad/s.               B. 3,14 Hz.                 C. 24 rad/s.               D. 0,628 rad/s.

Lời giải:
\(m = 100g; x = 5 \cos (\omega t + \frac{\pi}{3})\ (cm)\)
\(t = 0 \Rightarrow |F_{KV}| = 1 N \Rightarrow m\omega ^2|x_0| = 1\)
Với \(t = 0 \Rightarrow x = 2,5 \ cm \Rightarrow 0,1\omega ^2 . 2,5.10^{-2} = 1\)
\(\Rightarrow \omega = 20 \frac{rad}{s}\)
⇒ Chọn A

Câu 15: Một chất điểm dao động điều hòa theo phương trình \(x = 4\cos \frac{2\pi }{3}t\) (x tính bằng cm; t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = -2 cm lần thứ 2011 tại thời điểm
A. 3015 s.                   B. 6030 s.                   C. 3016 s.                   D. 6031 s.

Lời giải:
\(x=4\cos \frac{2\pi}{3}t \ (cm;s) \Rightarrow T = \frac{2\pi }{\omega } = 3s\)
\(\left\{\begin{matrix} x = -2 \ cm\\ t_{2011} = \ ? \ \ \ \end{matrix}\right.\)
t = 0, x = 4, v = 0

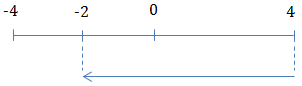
                         \(t_1 = \frac{T}{4}+\frac{T}{12} = \frac{T}{3}\)
\(\Rightarrow t_{2011} = t_1 + 2010 \frac{T}{2} = \left ( \frac{1}{3}+1005 \right )T = 3016s\)
⇒ Chọn C

Câu 16: Một chất điểm dao động dọc theo trục Ox. Phương trình dao động là \(x = 5\cos(8 \pi t - \frac{\pi}{6})\)(cm). Thời gian ngắn nhất vật đi từ lúc bắt đầu xét dao động đến lúc vật có li độ x = 2,5 cm là
A. \(\frac{3}{8}s\)                          B. \(\frac{1}{16}s\)                         C. \(\frac{8}{3}s\)                          D. \(\frac{1}{12}s\)

Lời giải:
\(x = 5\cos (8 \pi t - \frac{\pi}{6})\ (cm)\)
\(t=0: x = 2,5\sqrt{3}\ cm; v >0; T = \frac{2\pi}{\omega } = \frac{1}{4}s\)

\(\Delta t_{min} = \frac{T}{12} + \frac{T}{6} = \frac{T}{4} = \frac{1}{16}s\)
⇒ Chọn B

Câu 17: Một vật dao động điều hòa với chu kì T và biên độ 5 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn gia tốc không vượt quá 100 cm/s2 là \(\frac{T}{3}\). Lấy \(\pi ^2 = 10\). Tần số dao động của vật là
A. 4 Hz.                      B. 3 Hz.                      C. 1 Hz.                      D. 2 Hz.

Lời giải:
A = 5 cm

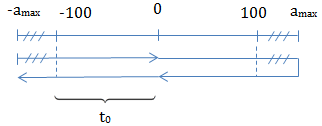
\(\Rightarrow \Delta t_0 = \frac{T}{3} \Rightarrow t_0 = \frac{T}{12} \Rightarrow \frac{a_{max}}{2} = 100\)
\(a_{max} = \omega ^2A =200 \Rightarrow \omega = 2\pi \frac{rad}{s} \Rightarrow f = 1Hz\)
⇒ Chọn C

Câu 18: Vật nhỏ của một con lắc lò xo dao động điều hòa theo phương ngang, mốc thế năng tại vị trí cân bằng. Khi gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại thì tỉ số giữa động năng và thế năng của vật là
A. \(\frac{1}{2}\)                           B. 3.                            C. 2.                            D. \(\frac{1}{3}\)

Lời giải:
\(|a| = \frac{a_{max}}{2}\Rightarrow \omega ^2 |x| = \frac{\omega ^2A}{2} \Rightarrow |x| = \frac{A}{2}\)

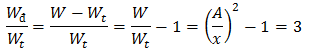
⇒ Chọn B

Câu 19: Vật dao động điều hòa với phương trình \(x = 5\cos(4 \pi t + \frac{\pi}{6})\) cm. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian S?
A. 5 cm                             B. \(5\sqrt{2}\) cm                  C. \(5\sqrt{3}\) cm                 D. 10 cm

Lời giải:
\(x = 5\cos (4\pi t + \frac{\pi}{6}) \ (cm);T = \frac{2\pi}{\omega } = \frac{1}{2}s\)
\(\Delta t = \frac{1}{8}s < \frac{T}{2} = \frac{1}{4}s \Rightarrow S_{max} = 2.5\sin (\frac{\pi}{T}\Delta t)\)
\(\Rightarrow S_{max} = 10\sin (\frac{\pi}{4}) = 5\sqrt{2}\)
⇒ Chọn B

Câu 20: Một chất điểm dao động điều hòa với biên độ A = 10 cm; chu kỳ T = 0,4 s. Trong khoảng thời gian 0,1 s vật không thể đi được quãng đường bằng bao nhiêu?
A. 4 cm                             B. 10 cm                      C. 12 cm                     D. 7,5 cm

Lời giải:
A = 10 cm; T = 0,4s
\(\Delta t = 0,1s = \frac{T}{4}\)
\(\Rightarrow S_{max } = 2.10\sin \left ( \frac{\pi}{T}.\Delta t \right ) = 10\sqrt{2} \ (cm)\) và \(\Rightarrow S_{min} = 2.10\left [ 1- \cos \left ( \frac{\pi}{T}.\Delta t \right ) \right ] = 20-10\sqrt{2} \ (cm)\)
\(S_{min} \leq S \leq S_{max} \Rightarrow 20-10\sqrt{2} \leq S \leq 10\sqrt{2}\)
⇒ Chọn A