Câu hỏi trắc nghiệm (40 câu):
-
Câu 1: Mã câu hỏi: 453891
Cho hàm bậc ba \(y = f\left( x \right)\) có đồ thị đạo hàm \(y = f'\left( x \right)\) như hình vẽ bên dưới. Hàm số nghịch biến trên khoảng nào?
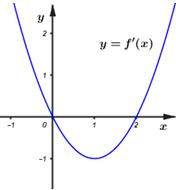
- A. \(\left( {1;{\mkern 1mu} {\mkern 1mu} 2} \right)\)
- B. \(\left( { - 1;{\mkern 1mu} {\mkern 1mu} 0} \right)\)
- C. \(\left( {3;{\mkern 1mu} {\mkern 1mu} 4} \right)\)
- D. \(\left( {2;{\mkern 1mu} {\mkern 1mu} 3} \right)\)
-
Câu 2: Mã câu hỏi: 453894
Cho biết khối lập phương có bao nhiêu mặt đối xứng?
- A. 6
- B. 9
- C. 8
- D. 10
-
Câu 3: Mã câu hỏi: 453898
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở \(B\), cạnh \(AC = 2a\). Cạnh SA vuông góc với mặt đáy \((ABC)\), tam giác SAB cân. Tính thể tích hình chóp S.ABC theo \(a\)?
- A. \(\dfrac{{2\sqrt 2 {a^3}}}{3}\).
- B. \(\dfrac{{\sqrt 2 {a^3}}}{3}\).
- C. \(2\sqrt 2 {a^3}\).
- D. \({a^3}\sqrt 2 \).
-
Câu 4: Mã câu hỏi: 453901
Có bao nhiêu tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3x + 2\) song song với đường thẳng \(y = 9x - 14\)?
- A. 1
- B. 0
- C. 3
- D. 2
-
Câu 5: Mã câu hỏi: 453904
Giá trị nhỏ nhất của hàm số \(y = \dfrac{1}{4}{x^4} - \dfrac{{27}}{2}{x^2} + 3\) trên đoạn \(\left[ {0;80} \right]\) bằng?
- A. \( - \dfrac{{229}}{5}.\)
- B. \( - 180.\)
- C. \( - \dfrac{{717}}{4}.\)
- D. 3
-
Câu 6: Mã câu hỏi: 453907
Hình chóp tam giác đều S.ABC có cạnh đáy là a và cạnh bên tạo với đáy một góc \({45^0}\). Tính theo \(a\) thể tích khối chóp S.ABC?
- A. \(\dfrac{{{a^3}}}{4}\)
- B. \(\dfrac{{{a^3}}}{{12}}\)
- C. \(\dfrac{{{a^3}}}{8}\)
- D. \(\dfrac{{{a^3}}}{{24}}\)
-
Câu 7: Mã câu hỏi: 453909
Cho hàm số \(y = {\rm{\;}} - {x^4} + 2{x^2} + 3.\) Mệnh đề nào sau đây là đúng?
- A. Đồ thị hàm số có 1 điểm cực đại và không có điểm cực tiểu.
- B. Đồ thị hàm số có 1 điểm cực tiểu và 2 điểm cực đại.
- C. Đồ thị hàm số có 1 điểm cực tiểu và không có điểm cực đại.
- D. Đồ thị hàm số có 1 điểm cực đại và 2 điểm cực tiểu.
-
Câu 8: Mã câu hỏi: 454021
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(A,{\mkern 1mu} {\mkern 1mu} BC = 2AB = 2a.\) Cạnh bên SC vuông góc với đáy, góc giữa SA và đáy bằng \({60^0}.\) Thể tích khối chóp đó bằng?
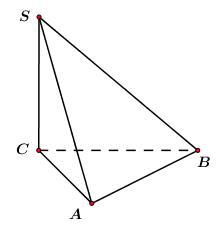
- A. \(\dfrac{{3{a^3}\sqrt 3 }}{2}\)
- B. \(\dfrac{{{a^3}\sqrt 5 }}{2}\)
- C. \(\dfrac{{{a^3}\sqrt 3 }}{6}\)
- D. \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
-
Câu 9: Mã câu hỏi: 454025
Cho khối hộp ABCD.A'B'C'D'. Gọi \(V,{\mkern 1mu} {\mkern 1mu} V'\) lần lượt là thể tích của khối hộp ABCD.A'B'C'D' và thể tích của khối chóp A'ABC'D'. Khi đó?
- A. \(\dfrac{{V'}}{V} = \dfrac{1}{3}\)
- B. \(\dfrac{{V'}}{V} = \dfrac{2}{7}\)
- C. \(\dfrac{{V'}}{V} = \dfrac{2}{5}\)
- D. \(\dfrac{{V'}}{V} = \dfrac{1}{4}\)
-
Câu 10: Mã câu hỏi: 454030
Giá trị nhỏ nhất của hàm số \(y = \sin x\) trên đoạn \(\left[ {0;\pi } \right]\) là?
- A. \( - 1\)
- B. \(\dfrac{1}{2}\)
- C. \(0\)
- D. \(1\)
-
Câu 11: Mã câu hỏi: 454063
Mỗi cạnh của hình đa diện là cạnh chung của?
- A. Hai mặt.
- B. Năm mặt.
- C. Ba mặt.
- D. Bốn mặt.
-
Câu 12: Mã câu hỏi: 454064
Cho hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\). Tìm phương trình tiếp tuyến với đồ thị hàm số tại điểm \(M\left( {2;3} \right)\)?
- A. \(y = 2x - 1\)
- B. \(y = {\rm{\;}} - 3x + 9\)
- C. \(y = 3x - 3\)
- D. \(y = {\rm{\;}} - 2x + 7\)
-
Câu 13: Mã câu hỏi: 454065
Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
- A. 6
- B. 2
- C. 8
- D. 4
-
Câu 14: Mã câu hỏi: 454066
Điểm cực tiểu của hàm số \(y = {x^3} - 3x - 2\) là?
- A. \(M\left( {1; - 4} \right)\)
- B. \(y = {\rm{\;}} - 4\)
- C. \(x = 1\)
- D. \(x = {\rm{\;}} - 1\)
-
Câu 15: Mã câu hỏi: 454067
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = \dfrac{{a\sqrt 3 }}{2}\), tam giác ABC đều cạnh bằng \(a\) (minh họa như hình dưới). Góc tạo bởi giữa mặt phẳng\((SBC)\) và \(\left( {ABC} \right)\) bằng?
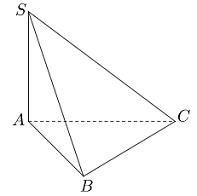
- A. \({90^{\rm{o}}}\).
- B. \({30^{\rm{o}}}\).
- C. \({45^{\rm{o}}}\).
- D. \({60^{\rm{o}}}\).
-
Câu 16: Mã câu hỏi: 454087
Hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 1} \right)\left( {{x^2} - 4} \right)\left( {{x^2} + x} \right),{\mkern 1mu} {\mkern 1mu} x \in \mathbb{R}\). Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
- A. \(6\)
- B. \(5\)
- C. \(3\)
- D. \(4\)
-
Câu 17: Mã câu hỏi: 454099
Cho hàm số \(y = \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\). Tổng số đường TCĐ và TCN của đồ thị hàm số đã cho là?
- A. \(3\)
- B. \(2\)
- C. \(5\)
- D. \(4\)
-
Câu 18: Mã câu hỏi: 454106
Đồ thị hàm số nào sau đây có 3 đường tiệm cận?
- A. \(y = \dfrac{{2 - x}}{x}\).
- B. \(y = \dfrac{x}{{{x^2} - x + 1}}\).
- C. \(y = \dfrac{1}{{{x^2} - 1}}\).
- D. \(y = \dfrac{{x - 1}}{{x + 1}}\).
-
Câu 19: Mã câu hỏi: 454111
Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực?
- A. \(y = {\rm{\;}} - {x^3} + 2{x^2} - 10x + 4\)
- B. \(y = \dfrac{{x + 10}}{{x - 1}}\)
- C. \(y = {x^2} - 5x + 6\)
- D. \(y = x + 5\)
-
Câu 20: Mã câu hỏi: 454115
Khối chóp S.ABC có đáy tam giác vuông cân tại \(B\) và \(AB = a.\)\(SA \bot \left( {ABC} \right)\). Góc giữa cạnh bên SB và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^0}\). Khi đó khoảng cách từ \(A\)đến \(\left( {SBC} \right)\) là?
- A. \(\sqrt 3 a\)
- B. \(\dfrac{{a\sqrt 3 }}{3}\)
- C. \(\dfrac{{a\sqrt 3 }}{2}\)
- D. \(\dfrac{{a\sqrt 2 }}{2}\)
-
Câu 21: Mã câu hỏi: 454118
Cho hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\). Khẳng định nào sau đây đúng?
- A. Hàm số đã cho nghịch biến trên từng khoảng xác định.
- B. Hàm số đã cho nghịch biến trên \(\mathbb{R}\).
- C. Hàm số đã cho nghịch biến trên tập \(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right).\)
- D. Hàm số đã cho đồng biến trên từng khoảng xác định.
-
Câu 22: Mã câu hỏi: 454119
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
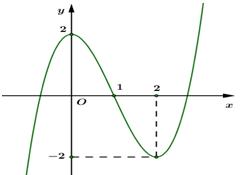
- A. \(y = {\rm{\;}} - {x^3} + 3{x^2} + 2\)
- B. \(y = {x^3} - 3x + 2\)
- C. \(y = {\rm{\;}} - {x^4} + 2{x^2} - 2\)
- D. \(y = {x^3} - 3{x^2} + 2\)
-
Câu 23: Mã câu hỏi: 454121
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm là \(f'\left( x \right) = {x^2}\left( {{x^2} - 4} \right)\left( {{x^2} - 3x + 2} \right)\left( {x - 3} \right)\). Hàm số có bao nhiêu điểm cực đại?
- A. 1
- B. 2
- C. 0
- D. 3
-
Câu 24: Mã câu hỏi: 454124
Hàm số \(y = {x^3} - 3x + 5\) đồng biến trên khoảng nào dưới đây?
- A. \(\left( { - 1; + \infty } \right)\)
- B. \(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\)
- C. \(\left( { - \infty ; - 1} \right)\)và \(\left( {1; + \infty } \right)\)
- D. \(\left( { - \infty ;1} \right)\)
-
Câu 25: Mã câu hỏi: 454127
Số giá trị nguyên của tham số \(m\) để hàm số \(y = {\rm{\;}} - \dfrac{1}{3}{x^3} + m{x^2} - \left( {3 + 2m} \right)x - 2020\) nghịch biến trên \(\mathbb{R}\) là?
- A. 5
- B. 4
- C. 2
- D. 3
-
Câu 26: Mã câu hỏi: 454132
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \(\left( {0;\sqrt 2 } \right)\)?
- A. \(y = \dfrac{{{x^2} + x - 1}}{{x - 1}}\)
- B. \(y = \dfrac{{2x - 5}}{{x + 1}}\)
- C. \(y = \dfrac{1}{2}{x^4} - 2{x^2} + 3\)
- D. \(y = \dfrac{3}{2}{x^3} - 4{x^2} + 6x + 9\)
-
Câu 27: Mã câu hỏi: 454137
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên:
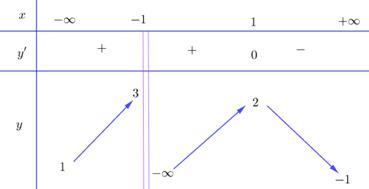
Khẳng định nào sau đây là đúng?
- A. Đồ thị hàm số đã cho có hai tiệm cận ngang.
- B. Hàm số đạt cực đại tại \(x = 2\).
- C. Giá trị lớn nhất của hàm số là 3.
- D. Đồ thị hàm số không có tiệm cận đứng.
-
Câu 28: Mã câu hỏi: 454140
Biết rằng hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị là đường cong như hình vẽ bên dưới.
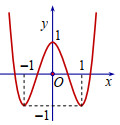
Tính giá trị \(f\left( {3a + 2b + c} \right)\)?
- A. \(f\left( {3a + 2b + c} \right) = {\rm{\;}} - 1\)
- B. \(f\left( {3a + 2b + c} \right) = {\rm{\;}} - 144\)
- C. \(f\left( {3a + 2b + c} \right) = {\rm{\;}} - 113\)
- D. \(f\left( {3a + 2b + c} \right) = 1\)
-
Câu 29: Mã câu hỏi: 454142
Cho khối lăng trụ tam giác đều ABC.A'B'C' có \(AB = a\)và \(AA' = 2a\). Thể tích của khối lăng trụ ABC.A'B'C' bằng?
- A. \(\dfrac{{{a^3}\sqrt 3 }}{2}.\)
- B. \({a^3}\sqrt 3 .\)
- C. \(\dfrac{{{a^3}\sqrt 3 }}{{12}}.\)
- D. \(\dfrac{{{a^3}\sqrt 3 }}{6}.\)
-
Câu 30: Mã câu hỏi: 454160
Gọi \(M,{\mkern 1mu} {\mkern 1mu} m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^2} + x + 3}}{{x - 2}}\) trên \(\left[ { - 2;{\mkern 1mu} {\mkern 1mu} 1} \right].\) Giá trị của \(M + m\) bằng?
- A. \( - 5\)
- B. \( - \dfrac{9}{4}\)
- C. \( - 6\)
- D. \( - \dfrac{{25}}{4}\)
-
Câu 31: Mã câu hỏi: 454164
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng \({45^0}\). Thể tích khối chóp đã cho bằng?
- A. \(\dfrac{{{a^3}}}{3}\)
- B. \(\dfrac{{4{a^3}}}{3}\)
- C. \(4{a^3}\)
- D. \(2{a^3}\)
-
Câu 32: Mã câu hỏi: 454168
Trong các loại khối đa diện đều sau, tìm khối đa diện có số cạnh gấp đôi số đỉnh?
- A. Khối hai mươi mặt đều.
- B. Khối lập phương.
- C. Khối mười hai mặt đều.
- D. Khối bát diện đều.
-
Câu 33: Mã câu hỏi: 454176
Giá trị cực tiểu \({y_{c{\rm{r}}}}\) của hàm số \(y = {x^3} - 3{{\rm{x}}^2} + 7\) là?
- A. \({y_{c{\rm{r}}}} = 2\)
- B. \({y_{c{\rm{r}}}} = 3\).
- C. \({y_{c{\rm{r}}}} = 0.\)
- D. \({y_{c{\rm{r}}}} = 7\).
-
Câu 34: Mã câu hỏi: 454181
Cho hàm số \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}}\). Số giá trị thực của \(m\) để đồ thị hàm số có đúng hai đường tiệm cận?
- A. 2
- B. 3
- C. 0
- D. 1
-
Câu 35: Mã câu hỏi: 454187
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), \(AA' = a\sqrt 2 .\) Khoảng cách giữa A'B và CC' bằng?
- A. \(\dfrac{{a\sqrt 3 }}{2}.\)
- B. \(a\sqrt 3 .\)
- C. \(a\)
- D. \(\dfrac{{a\sqrt 6 }}{3}.\)
-
Câu 36: Mã câu hỏi: 454190
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \dfrac{{mx + 9}}{{4x + m}}\) nghịch biến trên khoảng \(\left( {0;4} \right)\)?
- A. 5
- B. 11
- C. 6
- D. 7
-
Câu 37: Mã câu hỏi: 454196
Tìm điều kiện của tham số \(m\) để đường cong \(y = {x^4} - 4m{x^2} + 3m - 2\) có ba điểm cực trị \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) phân biệt sao cho tam giác ABC nhận \(G\left( {0; - \dfrac{5}{3}} \right)\) làm trọng tâm?
- A. \(m = 1\)
- B. \(m = 1\) hoặc \(m = 0,125\)
- C. \(m = 0,125\)
- D. \(m = 8\)
-
Câu 38: Mã câu hỏi: 454203
Tìm tất cả các giá trị của tham số m để hàm số \(y = {x^3} - m{x^2} + \left( {2m - 3} \right)x - 3\) đạt cực đại tại điểm \(x = 1\)?
- A. \(m \ge 3\)
- B. \(m > 3\)
- C. \(m < 3\)
- D. \(m \le 3\)
-
Câu 39: Mã câu hỏi: 454207
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt?
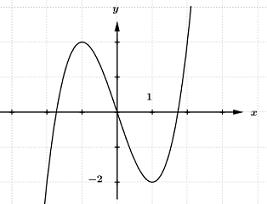
- A. \(m > 2.\)
- B. \(m < {\rm{\;}} - 1.\)
- C. \( - 1 < m < - \dfrac{1}{3}.\)
- D. \(1 < m < 2.\)
-
Câu 40: Mã câu hỏi: 454210
Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(2a\). Tam giác \(SAB\) nằm trên mặt phẳng vuông góc với đáy và có \(SA = a,{\mkern 1mu} {\mkern 1mu} \,\,SB = a\sqrt 3 .\) Tính V khối chóp \(SACD\)?
- A. \(\dfrac{{{a^3}\sqrt 3 }}{3}.\)
- B. \(\dfrac{{2{a^3}\sqrt 3 }}{3}.\)
- C. \(\dfrac{{{a^3}\sqrt 2 }}{3}.\)
- D. \(\dfrac{{{a^3}\sqrt 2 }}{6}.\)






