Bài toán Sơ đồ thời gian là ứng dụng mối quan hệ giữa chuyển động tròn đều và dao động điều hòa, chúng ta sẽ thiết lập sơ đồ về thời gian giữa các vị trí. Từ sơ đồ thời gian đó giải nhanh bài toán tìm thời điểm vật qua vị trí x₀ lần thứ n.

Sơ đồ thời gian là cái quan trọng nhất sau khi chúng ta chứng minh xong các em nên học thuộc luôn bởi vì nó đã chính xác, giúp các em làm tốt bài tập.

* Từ mối liên hệ giữa chuyển động tròn đều và DĐĐH \(\Rightarrow \Delta t = \frac{\alpha }{2\pi}.T\)

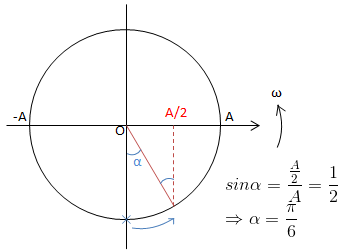
\(\\ \cdot \ x = 0 \Rightarrow x = \frac{A}{2} \Rightarrow \alpha = \frac{\pi}{6} \Rightarrow \Delta t = \frac{T}{12}\\ \cdot \ x = 0 \Rightarrow x = \frac{A}{\sqrt{2}} \Rightarrow \alpha = \frac{\pi}{4} \Rightarrow \Delta t = \frac{T}{8}\\ \cdot \ x = 0 \Rightarrow x = \frac{A\sqrt{3}}{2} \Rightarrow \alpha = \frac{\pi}{3} \Rightarrow \Delta t = \frac{T}{6}\\ \cdot \ x = 0 \Rightarrow x = A \Rightarrow \alpha = \frac{\pi}{2} \Rightarrow \Delta t = \frac{T}{4}\)
Tổng quát: \(\Delta t = \frac{\alpha }{2 \pi }.T\)

* Sơ đồ thời gian

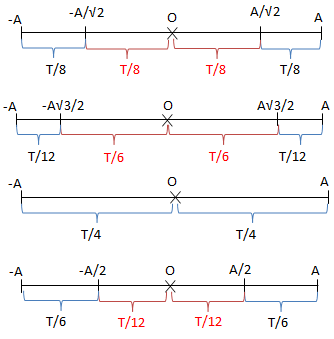
* Tìm thời điểm vật qua vị trí x₀ lần thứ n
Cho dao động: \(x = Acos(\omega t + \varphi )\)
Cách 1: Khi \(x = x_0 \Rightarrow cos(\omega t + \varphi ) = \frac{x_0}{A} \ \ (*)\)
Giải (*) ⇒ Tìm kết quả
Cách 2: Sử dụng sơ đồ thời gian
+ Xác định trạng thái ban đầu (t = 0)
+ Vẽ sơ đồ, xác định x₀
+ Vẽ đường đi ⇒ kết quả
* Chú ý:
(1) Khi không xét chiều chuyển động tại x₀ \((x_0 \neq \pm A)\).
Suy ra \(t_n = t_1 + \frac{n-1}{2}.T\): n là số lẻ
hoặc \(t_n = t_2 + \frac{n-1}{2}.T\): n là số chẵn
(2) Khi có xét chiều chuyển động tại x₀ ⇒ t_n = t₁ + (n – 1)T

VD1: Cho dao động \(x= 2\sqrt{2}.cos(10\pi t - \frac{\pi}{3})\) (cm).
a. Tìm thời điểm vật qua vị trí cân bằng lần 2015?
b. Tìm thời điểm vật qua vị trí x = -2cm lầm 2016?
Giải:
Cách 1:
a. Vật qua VTCB \(x = 0 \Rightarrow cos(10\pi t - \frac{\pi}{3}) = 0\)
\(\\ \Rightarrow 10\pi t - \frac{\pi}{3} = \frac{\pi}{2} + k \pi\\ \Leftrightarrow 10 \pi t = \frac{5 \pi }{6} + k \pi \Rightarrow t = \frac{1}{12} + \frac{k}{10} \ (Voi \ k \in Z; t > 0)\)
\(\\ \cdot \ k = 0 \Rightarrow t_1 = \frac{1}{12} + \frac{0}{10}\\ \cdot \ k = 1 \Rightarrow t_2 = \frac{1}{12} + \frac{1}{10}\\ \cdot \ k = 2 \Rightarrow t_3 = \frac{1}{12} + \frac{2}{10}\\ \vdots\\ \Rightarrow k = 2014 \Rightarrow t_{2015} = \frac{1}{12} + \frac{2014}{10} = \frac{12089}{60}s\)
b.
\(\left\{\begin{matrix} x = -2 \Rightarrow cos(10\pi t - \frac{\pi}{3}) = -\frac{1}{\sqrt{2}}\\ t_{2016} = \ ? \hspace{4,2cm} \end{matrix}\right.\)
\(\Rightarrow cos(10\pi t - \frac{ \pi }{3}) = cos \frac{3 \pi }{4}\)
\(\Rightarrow \Bigg \lbrack \begin{matrix} 10\pi t - \frac{\pi}{3} = - \frac{3 \pi}{4} + k2 \pi\\ 10\pi t - \frac{\pi}{3} = \frac{3 \pi}{4} + k2 \pi \ \ \end{matrix}\)
\(\Rightarrow \Bigg \lbrack \begin{matrix} 10\pi t = - \frac{5 \pi}{12} + k2 \pi\\ 10\pi t = \frac{13 \pi}{12} + k2 \pi \ \ \end{matrix}\)
\(\Rightarrow \Bigg \lbrack \begin{matrix} t = - \frac{1}{24} + \frac{k}{5}\\ t = \frac{13}{120} + \frac{k}{5}\ \end{matrix} \ \ \ (k \in Z; t > 0)\)
\(\\ \cdot \ k = 0: \Bigg \lbrack \begin{matrix} t_0 = - \frac{1}{24} + \frac{0}{5}\\ t_1 = \frac{13}{120} + \frac{0}{5}\ \end{matrix}\\ \cdot \ k = 1: \Bigg \lbrack \begin{matrix} t_2 = - \frac{1}{24} + \frac{1}{5}\\ t_3 = \frac{13}{120} + \frac{10}{5}\ \end{matrix}\\ \cdot \ k = 2: \Bigg \lbrack \begin{matrix} t_4 = - \frac{1}{24} + \frac{2}{5}\\ t_5 = \frac{13}{120} + \frac{2}{5}\ \end{matrix}\)
\(\Rightarrow t_{2n} = -\frac{1}{24} + \frac{n}{5}\)
Với 2016 = 2n  ⇒ n = 1008
\(\Rightarrow t_{2016} = -\frac{1}{24} + \frac{1008}{5} = \frac{24187}{120}(s)\)
Cách 2:
a.
\(\left\{\begin{matrix} x=0\\ t_{2015} = \ ? \end{matrix}\right.\)
\(t = 0: \left\{\begin{matrix} x = \sqrt{2}\\ v > 0 \ \ \end{matrix}\right.\)

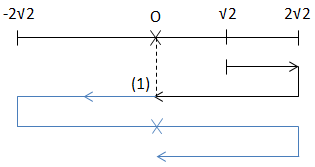
\(\\ t_1 = \frac{T}{6} + \frac{T}{4} = \frac{5T}{12}\\ \Rightarrow t_{2015} = t_1 + \frac{2014}{2}.T\\ \Rightarrow t_{2015} = \left ( \frac{5}{12} + \frac{2014}{2} \right ).T\\ \Rightarrow t_{2015} = \frac{12089}{60}s\)
b.

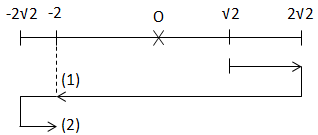
\(\\ t_2 = \frac{T}{6} + \frac{T}{2} + \frac{T}{8}= \frac{19T}{24}\\ \Rightarrow t_{2016} = t_2 + \frac{2016 - 2}{2}.T = \left ( \frac{19}{24} + 1007 \right ). \frac{1}{5} = \frac{24187}{120} (s)\)

VD2: Cho dao động \(x = 3.cos(4 \pi t + \frac{ \pi }{6})\) (cm). Tìm thời điểm vật qua vị trí \(x = -1,5\sqrt{3}\) cm và đang ra xa VTCB lần thứ 2016?
Giải:
\(\left\{\begin{matrix} x = -1,5\sqrt{3}\\ v < 0 \hspace{1,3cm}\\ t_{2016} = \ ? \hspace{0,6cm} \end{matrix}\right.\)
Cách 1:
\(\\ \Rightarrow \left\{\begin{matrix} cos(4 \pi t + \frac{\pi}{6}) = -\frac{\sqrt{3}}{2}\\ sin (4 \pi t + \frac{\pi}{6}) > 0 \ \ \ \ \end{matrix}\right. \\ \Rightarrow 4 \pi t + \frac{\pi}{6} = \frac{5 \pi }{6} + k2 \pi\\ \Rightarrow 4 \pi t = \frac{2 \pi}{3} + k2 \pi\\ \Rightarrow t = \frac{1}{6} + \frac{k}{2},\ (k \in Z; t > 0)\\ \Rightarrow t_{2016} = \frac{1}{6} + \frac{2015}{2} = \frac{6046}{6} = \frac{3023}{3}\)
Cách 2:
\(\left\{\begin{matrix} x = -1,5\sqrt{3}\\ v < 0 \hspace{1,3cm} \end{matrix}\right. ; t = 0: \left\{\begin{matrix} x = 1,5\sqrt{3}\\ v < 0 \hspace{1cm} \end{matrix}\right.\)

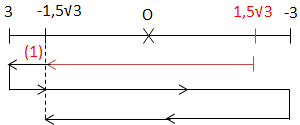
\(\Rightarrow t_{2016} = t_1 + (2016 - 1).T\)
Với \(\left\{\begin{matrix} t_1 = \frac{T}{6} + \frac{T}{6} = \frac{T}{3} \\ T = \frac{2 \pi}{3} = \frac{1}{2}s \ \ \ \ \end{matrix}\right.\)
\(\\ \Rightarrow t_{2016} = \left ( \frac{1}{3} + 2015 \right ).\frac{1}{2}\\ \Rightarrow t_{2016} = \frac{3023}{3}(s)\)