* Độ lêch pha

Gọi \(\varphi _1,\ \varphi _2\) lần lượt là độ lêch pha giữa u₁ và u₂ so với i.
+ Nếu \(\varphi _1 = \varphi _2\) ⇔ u₁ và u₂ cùng pha
⇒ \(\tan \varphi _1 = \tan \varphi _2\) ⇒ Kết quả
+ Nếu \(\varphi _1 - \varphi _2 = \pm \frac{\pi}{2}\) ⇔ u₁ và u₂ vuông pha
\(\Rightarrow \varphi _1 = \varphi _2 \pm \frac{\pi}{2} \Rightarrow \tan \varphi _1 = \tan \left (\varphi _2 \pm \frac{\pi}{2} \right ) = - \cot \varphi _2\)
\(\Rightarrow \tan \varphi 1 . \tan \varphi _2 = -1 \Rightarrow\) Kết quả
+ Nếu \(\varphi _1 - \varphi _2 = \varphi _{12}\) ⇔ u₁ lệch pha u₂ một góc \(\varphi _{12}\)
⇒ Vẽ giản đồ vecto ⇒ Kết quả

* Giản đồ vecto
Sử dụng dữ kiện đề bài → vẽ giản đồ → sử dụng toán học → kết quả.

VD1: Cho mạch điện: 
\(u_{AB} = U\sqrt{2} \cos (\omega t + \varphi )\ (V); \ U_{AM} + U_{MB} = U_{AB}\). Tìm hệ thức liên hệ giữa r₁, r₂, L₁, L₂?
Giải:
Ta có: \(\overrightarrow{U}_{AB} = \overrightarrow{U}_{AM} + \overrightarrow{U}_{MB}\)
Mà: \(U_{AB} = U_{AM} + U_{MB}\)
\(\Rightarrow \overrightarrow{U}_{AM} \nearrow \nearrow \overrightarrow{U}_{MB}\)
⇒ u_AM cùng pha u_MB \(\Rightarrow \tan \varphi _{AM} = \tan \varphi _{MB}\)
\(\Rightarrow \frac{Z_{L_{1}}}{r_1} = \frac{Z_{L_{2}}}{r_2} \Rightarrow \frac{L_1 \omega }{r_1} = \frac{L_2 \omega }{r_2} \Rightarrow \frac{L_1}{r_1} = \frac{L_2}{r_2}\)

VD2: Đặt điện áp \(u = U\sqrt{2} \cos \omega t\) vào 2 đầu doạn mạch gồm cuộn dây có điện trở R nối tiếp với tụ C thì U_d = U_C = U. Tìm hệ số công suất của mạch?
Giải:

U_RL = U_C = U

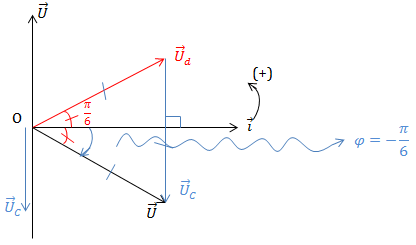
\(\Rightarrow \cos \varphi = \cos \left ( -\frac{\pi }{6} \right ) = \frac{\sqrt{3}}{2}\)

VD3: Đặt điện áp \(u=100\sqrt{6}\cos(100\pi t - \frac{\pi }{3})\) (V) vào 2 đầu đoạn mạch RLC ghép nói tiếp theo đúng thứ tự thì \(U_{RL}=\frac{U_C}{2} = 100V\). Viết biểu thức u_RL?
Giải:
\(\left\{\begin{matrix} U_{RL} = 100 V;\ U_C = 200 \hspace{1,2cm}\\ U = \frac{100\sqrt{6}}{\sqrt{2}}=100\sqrt{3};\ \varphi _U = -\frac{\pi}{3} \end{matrix}\right.\)
Nhận xét: \(U_{C}^{2}=U^2 + U_{RL}^{2}\Rightarrow \overrightarrow{U}\perp \overrightarrow{U}_{RL}\)

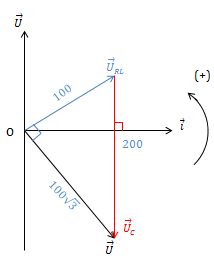
\(U_{0RL} = U_{RL}\sqrt{2}=100\sqrt{2}\ V\)
u_RL nhanh pha \(\frac{\pi}{2}\) so với u
\(\varphi _{U_{RL}} = \varphi _U + \frac{\pi }{2} = -\frac{\pi }{3} + \frac{\pi }{2}\)
\(\Rightarrow \varphi _{U_{RL}} = \frac{\pi }{6} \rightarrow u_{RL} = 100\sqrt{2}\cos (100 \omega t + \frac{\pi }{6})\)