Hôm nay chúng ta tìm hiểu dạng số 4 là dạng cuối cùng của con lắc đơn. Ở dạng số 3 chúng ta đã tìm hiểu sự thay đổi chu kỳ của con lắc đơn khi thay đổi độ cao, nhiệt độ; dạng số 2 ta nghiên cứu con lắc đơn trong trường hợp tổng quát; dạng số 1 chúng ta biến đổi những công thức thuần của chu kỳ, tần số con lắc đơn. Và ở dạng số 4 là dạng thay đổi chu kỳ của con lắc đơn khi chịu tác dụng của lực lạ F nào đó.

Ở trong đề thi sẽ có một số câu dạng như thế này, những câu này có thể được lặp đi lặp lại. Những câu dạng này thường khó vì là kiến thức lớp 10. Một câu trong đề thi liên quan đến kiến thức lớp 10 và 11 thường là câu khó.

* Khi chưa có lực lạ \(\overrightarrow{F}\)
Tại VTCB:
\(\overrightarrow{P} + \overrightarrow{T} = \overrightarrow{O}\)
\(\Rightarrow \overrightarrow{T} = - \overrightarrow{P}\)
\(\Rightarrow T = 2 \pi \sqrt{\frac{\ell}{g}}\)

* Khi đã chịu tác dụng của lực lạ \(\overrightarrow{F}\)
Tại VTCB:
\(\overrightarrow{P} + \overrightarrow{T} + \overrightarrow{F}= \overrightarrow{O}\)
\(\Rightarrow \overrightarrow{T} = - \underbrace{ ( \overrightarrow{P} + \overrightarrow{F}) }_{\overrightarrow{P}'} \Rightarrow \overrightarrow{T} = - \overrightarrow{P}'\)
\(\Rightarrow T' = 2\pi \sqrt{\frac{\ell}{g'}}\)
Với P' = mg': trọng lực hiệu dụng
       g': gia tốc hiệu dụng
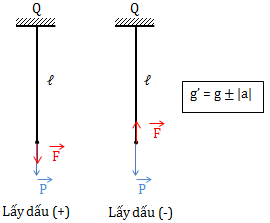
+ TH1: Lực \(\overrightarrow{F}\) có phương thẳng đứng và hướng xuống
Từ \(\overrightarrow{P}' = \overrightarrow{P} + \overrightarrow{F} \Rightarrow P' = P + F\)
Mà: P' = mg' ; P = mg ; F = ma
⇒ g' = g + |a|
+ TH2: Lực \(\overrightarrow{F}\) có phương thẳng đứng và hướng lên
Từ \(\overrightarrow{P}' = \overrightarrow{P} + \overrightarrow{F} \Rightarrow P' = P - F\)
\(\Rightarrow g ' = g \pm |a|\)

+ TH3: Lực \(\overrightarrow{F}\) có phương nằm ngang
Từ \(\overrightarrow{P}' = \overrightarrow{P} + \overrightarrow{F}\)
\(\Rightarrow g'^2 = g^2 + a^2\)
\(\Rightarrow g'= \sqrt{g^2 + a^2}\)

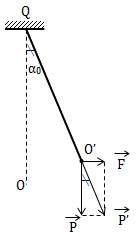
\(\cdot \ \cos \alpha _0 = \frac{P}{P'} = \frac{g}{g'}\)
\(\Rightarrow g' = \frac{g}{\cos \alpha _0} \Rightarrow \frac{T'}{T} = \sqrt{\frac{g}{g'}} = \sqrt{\cos \alpha _0}\)
\(\Rightarrow T' = T \sqrt{\cos \alpha _0}\)

* Các lực lạ thường gặp
+ Lực quán tính
\(\overrightarrow{F_{qt}} = -m\overrightarrow{a}\)
⇒ \(\overrightarrow{F_{qt}}\) ngược chiều gia tốc \(\overrightarrow{a}\)
• Chuyển động nhanh dần đều ⇒ v.a > 0
• Chuyển động chậm dần đều ⇒ v.a < 0
​+ Lực điện trường
\(\overrightarrow{F_{dt}} = q\overrightarrow{E}\)
• q > 0: \(\overrightarrow{F_{dt}}\) cùng chiều \(\overrightarrow{E}\)
• q < 0: \(\overrightarrow{F_{dt}}\) ngược chiều \(\overrightarrow{E}\)
+ Lực đây Acsimet
\(F_A = D.V.g\)

VD1: Một con lắc đơn gồm dây treo dài ℓ = 50 cm, quả cầu bằng kim loại nặng 10 g, được tích điện q = 5.10^-6C và đặt trong điện trường đều \(\overrightarrow{E}\) thẳng đứng hướng xuống, độ lớn E = 10⁴ V/m. Lấy g = 10 m/s²; \(\pi = 3,14\). Tìm chu kỳ con lắc này?
Giải:
ℓ = 50 cm = 0,5 m; m = 10 g = 0,01 kg
q = 5.10^-6C > 0 ⇒ \(\overrightarrow{F}\) cùng chiều \(\overrightarrow{E}\)
E = 10⁴ V/m
\(\overrightarrow{E}\) thẳng đứng hướng xuống \(\Rightarrow \overrightarrow{F} \nearrow \nearrow \overrightarrow{P}\)
\(\Rightarrow g' = g + a = g + \frac{F}{m} = g + \frac{|q|E}{m}\)
\(\Rightarrow g' = 10 + \frac{5.10^{-6}.10^4}{0,01} = 15\ m/s^2\)
\(\Rightarrow T' = 2\pi \sqrt{\frac{\ell}{g'}} = 2\pi \sqrt{\frac{0,5}{15}} = 1,15s\)

VD2: Một con lắc đơn treo trong thang máy, khi thang máy đứng yên thic hu kỳ T = 2s, khi thang máy đi xuống nhanh dần đều với gia tốc \(a = \frac{g}{2}\) (g là gia tốc trọng trường tại nơi đang xét) thì chu kỳ là T'. Tìm T'?
Giải:
Ta có: \(T = 2 \pi \sqrt{\frac{\ell}{g}}\)
           \(T' = 2 \pi \sqrt{\frac{\ell}{g'}}\)
\(\Rightarrow \frac{T'}{T} = \sqrt{\frac{g}{g'}}\)
Xuống nhanh dần đều \(\Rightarrow \left\{\begin{matrix} \overrightarrow{v} \downarrow\\ \overrightarrow{a} \downarrow \end{matrix}\right.\)
\(\overrightarrow{a} \downarrow \Rightarrow \overrightarrow{F_{qt}} \uparrow\)
\(\Rightarrow g' = g - |a| = g - \frac{g}{2} = \frac{g}{2}\)
\(\Rightarrow \frac{g}{g'} = 2\)
\(\Rightarrow \frac{T'}{T} = \sqrt{\frac{g}{g'}} = \sqrt{2}\)
\(\Rightarrow T' = T.\sqrt{2} = 2 \sqrt{2} \ (s)\)