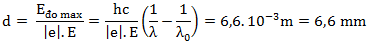Hôm nay chúng ta tiếp tục qua dạng bài tập thứ 3 của Hiện tượng quang điện, đây cũng là một trong các ứng dụng quan trọng của hiện tượng quang điện ngoài :Chuyển động của electron trong từ trường đều. Mời các em cùng tìm hiểu .
 Playlist:
THPT QG Vật lý - Chuyên đề Lượng tử...
Playlist:
THPT QG Vật lý - Chuyên đề Lượng tử...
-
Video liên quan
-
Nội dung
-
Bài 1: Tìm khoảng đơn điệu của hàm số

Bài 1: Tìm khoảng đơn điệu của hàm số
Bài giảng sẽ giúp các em nắm được kiến thức cơ bản về cách tìm khoảng đơn điệu của hàm số như: Định nghĩa Điều kiện đủ để hàm số đơn điệu Các bước tìm khoảng đơn điệu của hàm số00:55:29 5717 TS. Phạm Sỹ Nam
-
Bài 2: Tìm tham số để hàm số đơn điệu trên một miền

Bài 2: Tìm tham số để hàm số đơn điệu trên một miền
Bài giảng sẽ giúp các em nắm được kiến thức cơ bản về cách tìm tham số để hàm số đơn điệu trên một miền như: Công thức tính. Điều kiện đủ để hàm số đơn điệu trên một miền.00:28:42 1163 TS. Phạm Sỹ Nam
-
Bài 3: Ứng dụng tính đơn điệu giải phương trình

Bài 3: Ứng dụng tính đơn điệu giải phương trình
Bài giảng sẽ giúp các em nắm kỹ hơn về lý thuyết và một số ví dụ cụ thể về ứng dụng tính đơn điệu giải phương trình.00:32:49 1205 TS. Phạm Sỹ Nam
-
Bài 4: Ứng dụng tính đơn điệu giải bất phương trình

Bài 4: Ứng dụng tính đơn điệu giải bất phương trình
Bài giảng Ứng dụng tính đơn điệu giải bất phương trình sẽ giúp các em nắm được lý thuyết và bài tập để các em củng cố kiến thức.00:32:29 993 TS. Phạm Sỹ Nam
-
Bài 5: Ứng dụng tính đơn điệu giải hệ phương trình

Bài 5: Ứng dụng tính đơn điệu giải hệ phương trình
Bài giảng Ứng dụng tính đơn điệu giải hệ phương trình sẽ giúp các em nắm kỹ hơn cách giải hệ phương trình, cách tìm tính nghịch biến, đồng biến về tính đơn điệu của hệ phương trình.00:29:14 1074 TS. Phạm Sỹ Nam
-
Bài 6: Ứng dụng tính đơn điệu chứng minh bất đẳng thức

Bài 6: Ứng dụng tính đơn điệu chứng minh bất đẳng thức
Bài giảng ứng dụng tính đơn điệu chứng minh bất đẳng thức gồm có 2 phần nội dung chính: Lý thuyết Các ví dụ cụ thể nhằm giúp các em chứng minh được đồng biến và nghịch biến.00:43:58 1248 TS. Phạm Sỹ Nam
* Xét electron quang điện chuyển động với vận tốc \(\overrightarrow{v_0}\) trong vùng từ trường đều \(\overrightarrow{B}\ (\overrightarrow{B} \perp \overrightarrow{v_0})\)
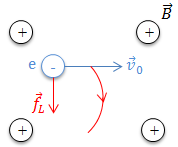
Electron quang điện chịu tác dụng của lực Lorenzt \(\overrightarrow{f}_L\), \(\overrightarrow{f}_L\) không sinh công mà đóng vai trò là lực hướng tâm làm electron chuyển động tròn đều
\(\Rightarrow f_L = F_{ht} \Rightarrow |e|.v_0.B = m.\frac{v_{0}^{2}}{R}\)
\(\Rightarrow R = \frac{mv_0}{|e|.B}\) Với \(\left\{\begin{matrix} m = m_e = 9,1.10^{-31}\ kg\\ |e| = 1,6.10^{-19}\ C \hspace{1,2cm} \end{matrix}\right.\)
Nếu \(v_{0\ max} \Rightarrow R_{max} = \frac{m.v_{0\ max}}{|e|.B}\)
* Chú ý: Nếu \(\overrightarrow{v}\) xiên góc với \(\overrightarrow{B}\)
\(\Rightarrow R = \frac{m.v_n}{|e|.B},\ \overrightarrow{v_n} \perp \overrightarrow{B}\)
Lúc này quỹ đạo là đường xoắn ốc
* Nếu electron chuyển động trong điện trường đều \(\overrightarrow{E}\) ⇒ Electron chịu tác dụng của lực điện trường \(\overrightarrow{F} = -|e|\overrightarrow{E}\)
Sử dụng định lý động năng: \(\Delta E_d = E_{d_1} - E_{d_2} = A_{\overrightarrow{F_{dt}}}\)
VD1: Chiếu một bức xạ đơn sắc có bước sóng \(\lambda\) vào tấm kim loại có giới hạn quang điện \(\lambda _0 = 2\lambda\). Các quan electron vừa bay ra được hướng vào vùng từ trường đều \(\overrightarrow{B} \perp \overrightarrow{v}\). Xác định biểu thức tính bán kính quỹ đạo của electron?
Giải:
Vận tốc quang electron: v0 max
\(R_{max} = \frac{m.v_{0\ max}}{|e|.B}\)
Mà: \(v_{0\ max} = \sqrt{\frac{2hc}{m}.\left ( \frac{1}{\lambda } - \frac{1}{\lambda _0} \right )} = \sqrt{\frac{2hc}{m.\lambda _0}}\)
\(\Rightarrow R_{max} = \frac{m}{|e|.B}. \sqrt{\frac{2hc}{m.\lambda _0}} = \frac{1}{|e|.B}. \sqrt{\frac{2hcm}{\lambda _0}}\)
VD2: Chiếu một bức xạ đơn sắc có \(\lambda =0,2 \ \mu m\) vào một tám kẽm có giới hạn quang điện \(\lambda _0 = 0,35 \ \mu m\). Electron vừa bật ra được hướng vào điện trường đều có độ lớn E = 400 V/m (\(\overrightarrow{E}\) cùng hướng \(\overrightarrow{v}\)). Tìm quãng đường electron đi được trong điện trường?
Giải:
Eđo max = \(\frac{hc}{\lambda } - \frac{hc}{\lambda _0}\)
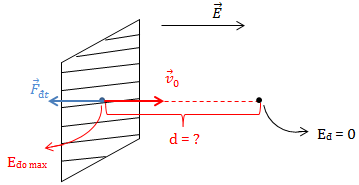
Ta có: Eđ - Eđo max = AFđt = -|e|.E.d
⇒ 0 - Eđo max = -|e|.E.d
⇒