-
Câu hỏi:
Trên một sợi dây đàn hồi đang có sóng dừng ổn định. Xét 3 phần tử A, B, C trên sợi dây: A là một nút sóng, B là bụng sóng gần A nhất, C ở giữa A và B. Khi sợi dây duỗi thẳng thì khoảng AB = 21,0cm và AB = 3AC. Khi sợi dây biến dạng nhiều nhất thì khoảng cách giữa A và C là 9,0cm. Tỉ số giữa tốc độ dao động cực đại của phần tử B và tốc độ truyền sóng trên dây xấp xỉ bằng
- A. 0,56
- B. 0,42
- C. 0,85
- D. 0,60
Lời giải tham khảo:
Đáp án đúng: C
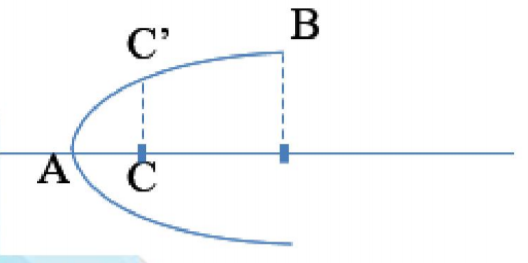
Ta có: \(AB=\frac{\lambda }{4}=21\text{cm}\Rightarrow \lambda =84\text{cm}\Rightarrow AC=\frac{AB}{3}=\frac{\lambda }{12}=7\text{cm}\)
Biên độ của B: \({{a}_{B}}=2\text{a}\) (điểm bụng)
Biên độ của C: \({{a}_{C}}=2a\sin \frac{2\pi d}{\lambda }=2a\sin \frac{2\pi \frac{\lambda }{12}}{\lambda }=a\)
Khi dây bị biến dạng nhiều nhất khi đó AC' = 9cm
Lại có: \(A{{C}^{\prime 2}}=A{{C}^{2}}+{{a}^{2}}\Rightarrow a=4\sqrt{2}cm\)
+ Tốc độ dao động cực đại của phần tử B: \({{v}_{B}}=2\text{a}\omega \)
+ Tốc độ truyền sóng trên dây: \(v=\lambda f=\lambda \frac{\omega }{2\pi }\)
\(\Rightarrow \) Tỉ số giữa tốc độ dao động cực đại của phần tử B và tốc độ truyền sóng: \(\frac{2a\omega }{\lambda \frac{\omega }{2\pi }}=\frac{4a}{\lambda }=\frac{4\pi .4\sqrt{2}}{84}=0,846\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Đơn vị của hiệu điện thế là
- Dao động của con lắc đồng hồ là dao động
- Một con lắc đơn chiều dài l đang dđ điều hòa tại nơi gia tốc rơi tự do g.
- Sóng cơ hình sin truyền theo dọc Ox với bước sóng \(\lambda \).
- Đặt vào hai đầu đoạn mạch R, L, C không phân nhánh một điện áp xoay chiều
- Dùng vôn kế xoay chiều đo điện áp giữa hai đầu của đoạn mạch xoay chiều
- Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R và tụ điện
- Khi ghép n nguồn điện giống nhau song song, mỗi nguồn có suất điện động
- Một con lắc lò xo nằm ngang DĐĐH có chiều dài biến thiên từ 20cm đến 26cm.
- Âm sắc của âm là một đặc trưng sinh lý của âm phụ thuộc vào
- Một vật có khối lượng m đang DĐĐH theo pt \(x=A\cos (\omega t+\varphi ).\)
- Trong một thí nghiệm giao thoa sóng với hai nguồn đồng bộ dao động
- Một máy biến áp lí tưởng có số vòng dây của cuộn sơ cấp và cuộn thứ cấp
- Đặt điện áp xoay chiều vào hai đầu đoạn mạch mắc nối tiếp gồm cảm kháng
- Cho hai dao động điều hòa cùng phương, cùng tần số, có biên độ lần lượt là A1 và A2
- Con lắc đơn có chiều dài l dao động điều hòa với biên độ góc
- Sóng cơ truyền trên một sợi dây rất dài với khoảng cách giữa hai đỉnh sóng liên tiếp là 20cm
- Một chất điểm dao động điều hòa trên trục Ox với phương trình chuyển động
- Đặt điện áp xoay chiều có tần số góc \(\omega \) vào hai đầu đoạn mạch
- Trên một sợi dây đàn hồi dài 1,6m hai đầu cố định, đang có sóng dừng.
- Một vật khối lượng 100g dao động điều hòa theo phương trình x = 3cos(2πt)
- Vật AB đặt vuông góc trục chính thấu kính hội tụ, cách thấu kính 20cm.
- Một mạch điện gồm nguồn điện có suất điện động 3V và điện trở trong là 1Ω.
- Trong không khí khi hai điện tích điểm đặt cách nhau là d và d +10cm
- Một khung dây dẫn phẳng, diện tích 50cm2, gồm 500 vòng dây
- Trong một thí nghiệm giao thoa với hai nguồn đồng bộ phát sóng kết hợp
- Một đoạn mạch gồm điện trở R = 50Ω, cuộn cảm có \(L=\frac{1}{\pi }H,\)
- Con lắc lò xo có độ cứng k = 40N/m treo thẳng đứng đang dao động điều hòa
- Cho mạch điện xoay chiều RLC mắc nối tiếp với cuộn cảm thuần, cho R = 50Ω.
- Một chất điểm thực hiện đồng thời hai dao động điều hòa có phương trình
- Một sóng ngang truyền trên sợi dây với tốc độ và biên độ không đổi
- Trong TN khảo sát chu kì dao động T của con lắc đơn, 1 HS làm thí nghiệm
- Một chất điểm dao động điều hòa có đồ thị li độ theo thời gian như hình vẽ
- Hai nguồn sóng kết hợp, đặt tại A và B cách nhau 20cm dao động theo pt:
- 1 máy biến áp lí tưởng có số vòng dây của cuộn sơ cấp có tổng số vòng dây
- Một sợi dây nhẹ không dãn có chiều dài 1,5m được cắt thành hai con lắc đơn
- Đặt điện áp \({{u}_{AB}}=40\sqrt{2}\cos (100\pi t)V\) vào hai đầu mạch AB
- CLLX treo thẳng đứng gồm lò xo nhẹ độ cứng 100N/m, đầu trên lò xo cố định
- Trên một sợi dây đàn hồi đang có sóng dừng ổn định. Xét 3 phần tử A, B, C
- Đặt một điện áp xoay chiều ổn định \(u=U\sqrt{2}\cos (\omega t)\) V
