Tại hai điểm A, B ở mặt chất lỏng có 2 nguồn kết hợp dao động điều hòa

​

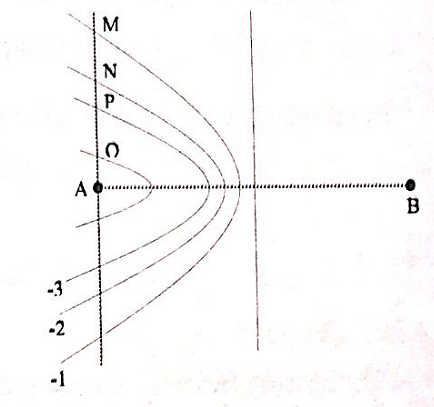
+ Vì M là điểm xa nhất nên M thuộc cực đại thứ nhất => k_M = -1

+ Vì N, P là các cực đại kế tiếp nên => k_N = -2; k_P = -3

+ Ta có:  

 \(\begin{array}{l}
\left\{ \begin{array}{l}
MA - MB =  - \lambda \\
NA - NB =  - 2\lambda \\
PA - PB =  - 3\lambda 
\end{array} \right.\\
 \Rightarrow \left\{ \begin{array}{l}
\left( {22,5 + 8,75 + PA} \right) - MB =  - \lambda \\
\left( {8,75 + PA} \right) - NB =  - 2\lambda \\
PA - PB =  - 3\lambda 
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
MB = \left( {31 + PA} \right) + \lambda \\
NB = \left( {8,75 + PA} \right) + 2\lambda {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( 1 \right)\\
PA - PB =  - 3\lambda 
\end{array} \right.
\end{array}\)

+ Lại có:  

\(\left\{ \begin{array}{l}
M{B^2} = {\left( {31 + PA} \right)^2} + A{B^2}\\
N{B^2} = {\left( {PA + 8,75} \right)^2} + A{B^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( 2 \right)\\
P{B^2} = P{A^2} + A{B^2}
\end{array} \right.\)

+ Từ (1) và (2), ta có:  

\(\begin{array}{*{20}{l}}
{\left\{ {\begin{array}{*{20}{l}}
{{{\left[ {\left( {31 + PA} \right) + \lambda } \right]}^2} = {{\left( {31 + PA} \right)}^2} + A{B^2}}\\
{{{\left[ {\left( {8,75 + PA} \right) + 2\lambda } \right]}^2} = {{\left( {PA + 8,75} \right)}^2} + A{B^2}}\\
{{{\left( {PA + 3\lambda } \right)}^2} = P{A^2} + A{B^2}}
\end{array}} \right.}\\
{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2\lambda \left( {31 + PA} \right) + {\lambda ^2} = A{B^2}}\\
{4\lambda \left( {8,75 + PA} \right) + 4{\lambda ^2} = A{B^2}}\\
{6.PA.\lambda  + 9{\lambda ^2} = A{B^2}}
\end{array}} \right.\begin{array}{*{20}{c}}
{\left( 3 \right)}\\
{\left( 4 \right)}\\
{\left( 5 \right)}
\end{array}}\\
{\left\{ {\begin{array}{*{20}{l}}
{2\left( {31 + PA} \right) = 4\left( {8,75 + PA} \right) + 3\lambda }\\
{2\left( {31 + PA} \right) + \lambda  = 9\lambda  + 6PA}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\lambda  = 4\left( {cm} \right)}\\
{PA = 7,5\left( {cm} \right)}
\end{array}} \right.}
\end{array}\)

+ Khoảng cách giữa hai nguồn AB:

\(AB = \sqrt {6.PA.\lambda  + 9{\lambda ^2}}  = 18\left( {cm} \right) \Rightarrow \frac{{AB}}{\lambda } = 4,5\) 

+ Suy ra cực đại ngoài cùng gần A nhất ứng với k_Q = -4

+ Ta có:

\(QA - QB =  - 4\lambda  \Leftrightarrow QA - \sqrt {Q{A^2} + {{18}^2}}  =  - 16 \Rightarrow QA = 2,125\left( {cm} \right)\)