-
Câu hỏi:
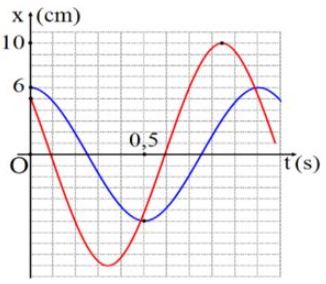
Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có đồ thị li độ của các dao động thành phần theo thời gian như hình vẽ. Khi đi qua vị trí cân bằng, vật có tốc độ là
- A. \(32\pi {\rm{cm}}/{\rm{s}}\)
- B. \(28\;{\rm{cm}}/{\rm{s}}\)
- C. \(32\;{\rm{cm}}/{\rm{s}}\)
- D. \(28\pi {\rm{cm}}/{\rm{s}}\)
Lời giải tham khảo:
Đáp án đúng: D
Đáp án : D
Từ hình vẽ: \(\frac{T}{2} = 0,5s \Rightarrow T = 1\left( s \right)\)
Tần số góc của hai dao động là:
\(\omega = \frac{{2\pi }}{T} = 2\pi \left( {rad/s} \right)\)
Biên độ của hai dao động: \({A_1} = 10cm,\,\,{A_2} = 6\,cm.\)
Lúc \(t = 0,\,\left\{ \begin{array}{l}{x_2} = 6cm = {A_1} \Rightarrow {\varphi _1} = 0\\\left\{ \begin{array}{l}{x_1} = 5cm = \frac{{{A_1}}}{2}\\{v_1} < 0\end{array} \right. \Rightarrow {\varphi _2} = \frac{\pi }{3}\end{array} \right.\)
Phương trình dao động của hai vật là:
\(\left\{ \begin{array}{l}{x_1} = 10\cos \left( {2\pi t + \frac{\pi }{3}} \right)\\{x_2} = 6\cos \left( {2\pi t} \right)\end{array} \right.\)
Biên độ dao động tổng hợp là:
\(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \left( {\overrightarrow {{A_1}} ,\overrightarrow {{A_2}} } \right)} \\ \Rightarrow A = \sqrt {{{10}^2} + {6^2} + 2.10.6.\cos \frac{\pi }{3}} = 14\left( {cm} \right)\end{array}\)
Khi đi qua vị trí cân bằng, vật có tốc độ là:
\({v_{\max }} = \omega A = 2\pi .14 = 28\pi \)(cm/s)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Bản chất của tia phóng xạ \(\alpha \) là
- Đặt điện áp xoay vào hai đầu đoạn mạch gồm điện trở thuần \(R = 40\Omega \) mắc nối tiếp với tụ điện thì dung kháng của tụ điện là \({Z_C} = 60\Omega \). Tổng trở của đoạn mạch là
- Xét nguyên tử hiđrô theo mẫu nguyên tử Bo, mức năng lượng của nó ở các trạng thái dừng theo thứ tự tăng dần từ giá trị nhỏ nhất là \({E_1},{E_2},{E_3} \ldots \) Nguyên tử hiđrô hấp thụ một phôtôn có năng lượng \(\varepsilon = {E_3} - {E_1}\) thì êlectron chuyển từ quỹ đạo
- Một sóng ngang truyền trên sợi dây rất dài với phương trình sóng \(u = A\cos \left( {20\pi t - \frac{\pi }{{10}}x} \right)\) (\(x\) tính bằng \({\rm{cm}},t\) tính bằng \({\rm{s}})\). Bước sóng trên sợi dây là
- Giới hạn quang điện của kim loại đồng là \(0,3\mu m\). Chiếu lần lượt các bức xạ có bước sóng (trong chân không) là \(0,50\mu m;\,\,0,28\mu m;\,\,0,35\mu m;\,\,0,41\mu m\) và \(0,19\mu m\) vào một tấm đồng. Số bức xạ gây ra được hiện tượng quang điện ngoài là
- Khoảng cách từ đài truyền hình Việt Nam (VTV) đến vệ tinh VINASAT-2 khoảng \(36.000\;{\rm{km}}\). Cho \(c = {3.10^8}\;m/s\). Thời gian để sóng vô tuyến truyền từ đài VTV đến vệ tinh có giá trị là
- Cấu tạo của buồng tối trong máy quang phổ lăng kính gồm
- Một chùm ánh sáng đơn sắc đỏ truyền trong chân không có bước sóng \(\lambda = 0,75\mu m\). Cho hằng số Plăng là \(h = 6,{625.10^{ - 34}}\;J.s;\,\,c = {3.10^8}\;m/s\). Năng lượng phôtôn của ánh sáng là
- Nguyên tắc hoạt động của máy phát điện xoay chiều ba pha dựa trên hiện tượng
- Một điện tích điểm \(q\) đặt ở điểm \(O\) trong chân không, tại điểm \(M\) cách \(O\) một đoạn \(r\) thì cường độ điện trường có độ lớn
- Đặt điện áp xoay chiều vào hai đầu cuộn thuần cảm thì cường độ dòng điện chạy qua cuộn cảm
- Dòng điện trong chất điện phân là dòng chuyển động có hướng
- Trong thí nghiệm giao thoa sóng ở mặt nước với hai nguồn kết hợp cùng pha, các vân giao thoa cực tiểu là những đường
- Hãy cho biết. Chức năng khuếch đại âm của hộp đàn ghita là dựa trên hiện tượng
- Hai dao động điều hoà cùng phương, cùng tần số, cùng pha thì có độ lệch pha bằng
- Một con lắc lò xo có độ cứng \(k\), khối lượng vật nhỏ \(m\) dao động điều hoà. Tại thời điểm mà li độ và vận tốc của vật tương ứng là \(x\) và \(v\) thì động năng của vật là
- Bước sóng của một sóng hình sin là quãng đường sóng truyền được trong
- Đặt khung dây dẫn phẳng, kín với diện tích \(S\) trong từ trường đều có cảm ứng từ \(B.\) Từ thông qua khung dây có độ lớn là \(\Phi = 0,8BS\). Góc giữa vectơ pháp tuyến của mặt phẳng khung dây với đường sức từ là
- Đặc trưng nào sau đây không phải là đặc trưng sinh lí của âm?
- Đặt vào hai đầu điện trở \(R\) một hiệu điện thế không đổi \(U\). Công suất toả nhiệt trên điện trở \(R\) là
- Phản ứng nhiệt hạch là phản ứng trong đó
- Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu mạch điện \(R,\,\,L,\,C\) mắc nối tiếp thì xảy ra cộng hưởng điện. Tổng trở của đoạn mạch lúc này bằng giá trị của
- Tia phóng xạ nào sau đây không bị lệch trong điện trường?
- Trong sơ đồ khối của một máy thu thanh vô tuyến đơn giản, mạch khuếch đại có tác dụng
- Hạt nhân Đơteri \({}_1^2D\) có khối lượng \(2,0136{\rm{ }}u.\) Biết khối lượng của prôtôn là \(1,0073u\) và khối lượng của nơtrôn là \(1,0087{\rm{ }}u.\) Độ hụt khối của hạt nhân \({}_1^2D\) bằng
- Tính chất nổi bật và quan trọng nhất của tia \(X\) là
- Một máy phát điện xoay chiều một pha có rô to là phần cảm gồm có 4 cặp cực quay với tốc độ \(12,5\)vòng/s. Tần số của suất điện động do máy phát sinh ra là:
- Khi chiếu ánh sáng có bước sóng thích hợp vào một chất thì điện trở suất của nó giảm. Chất này được gọi là
- Một con lắc đơn có chiều dài \(l = 80\,\,cm\) dao động điều hòa tại nơi có \(g = 9,81\;m/{s^2}\). Chu kỳ dao động của con lắc là
- Cho hạt nhân nguyên tử \({}_Z^AX\). Số nơtron trong hạt nhân nguyên tử bằng
- Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có đồ thị li độ của các dao động thành phần theo thời gian như hình vẽ. Khi đi qua vị trí cân bằng, vật có tốc độ là
- Đặt điện áp \(u = 6\sqrt 2 \cos \left( {\omega t} \right)\,\,V\) (\(\omega \) không đổi) vào hai đầu đoạn mạch gồm cuộn dây mắc nối tiếp với tụ điện. Điện áp hiệu dụng hai đầu cuộn dây là \(10\;{\rm{V}}\) và sớm pha hơn điện áp hai đầu mạch là \(1,56{\rm{rad}}.\)Hệ số công suất của mạch là
- Đặt điện áp xoay chiều (có giá trị hiệu dụng và tần số không đổi) vào hai đầu đoạn mạch như hình H.1 thì cảm kháng của cuộn dây \({Z_L} = 2r\). Gọi \(\varphi \) và \({\varphi _2}\) tương ứng là độ lệch pha giữa điện áp \({u_{AB}}\) và \({u_{MB}}\) so với cường độ dòng điện trong mạch. Đồ thị biểu diễn sự phụ thuộc của \(\varphi \) vào \({\varphi _2}\) khi điện dung \(C\) thay đổi như hình H.2. Khi \(C = {C_0}\) thì điện áp \({u_{AN}}\) lệch pha \({90^0}\) so với \({u_{MB}}\). Khi đó, hệ số công suất của đoạn mạch \(MB\) là
- Một vật dao động điều hoà với phương trình \(x = 6\cos \left( {2\pi t + \frac{\pi }{6}} \right){\rm{cm}}.\) Trên vật gắn với một nguồn sáng phát ánh sáng đơn sắc có tần số \({5.10^{14}}\) Hz, công suất \(0,53\)W. Biết hằng số Plăng là \(h = 6,{625.10^{ - 34}}\;{\rm{J}}{\rm{.s}}\)Tính từ thời điểm \(t = 0\) đến thời điểm gần nhất vật có li độ \( - 3\;{\rm{cm}}\) thì nguồn sáng phát số phôtôn gần nhất với giá trị nào sau đây?
- Một vật hình trụ tiết diện nhỏ, có chiều cao \(20\;{\rm{cm}}\), nổi thẳng đứng trong một bể nước rộng. Bỏ qua mọi lực cản, lấy \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\). Khi cân bằng, một nửa vật bị chìm trong nước và mép dưới của vật cách đáy bể một đoạn đủ dài. Từ vị trí cân bằng của vật, truyền cho nó vận tốc ban đầu bằng \(1,5\;{\rm{m}}/{\rm{s}}\) hướng thẳng đứng xuống dưới. Kể từ lúc vật bắt đầu chuyển động đến lúc vận tốc của vật triệt tiêu lần đầu tiên thì tốc độ trung bình của vật gần nhất với giá trị nào sau đây?
- Trong bài thí nghiệm thực hành 'Khảo sát thực nghiệm các định luật dao động của con lắc đơn', một nhóm học sinh đo thời gian 10 dao động toàn phần liên tiếp và thu được kết quả \(t = 18,025 \pm 0,247\;s\); đo chiều dài dây treo và thu được kết quả \(l = 0,81 \pm 0,01\;m.\) Cho số \(\pi = 3,140 \pm 0,026\). Gia tốc trọng trường tại nơi làm thí nghiệm mà nhóm học sinh này đo được là
- Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn đặt tại hai điểm \(A,B\) ở mặt nước dao động điều hòa cùng tần số, cùng pha. Hai điểm cực tiểu liên tiếp trên đoạn \(AB\) cách nhau \(2\;{\rm{cm}}\). Khoảng cách giữa hai nguồn là \(AB = 30\;{\rm{cm}}\). Xét các phần tử nước nằm trên trung trực của \(AB,\,\,{M_1},\,\,{M_2},\,\,{M_3}\) theo thứ tự đó là ba điểm liên tiếp mà phần tử mặt nước ở đó dao động cùng pha với nguồn. Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) gần nhất với giá trị nào sau đây?
- Một mạch dao động lí tưởng có độ tự cảm \(L = 4\mu {\rm{H}}\) và điện dung \(C\). Tại thời điểm \(t\) thì cường độ dòng điện tức thời là \(2\;{\rm{mA}}\), tại thời điểm \(t + \frac{{\pi \sqrt {LC} }}{2}\) thì điện áp tức thời trên tụ điện là \(1\;{\rm{V}}\). Giá trị của \(C\) là
- Một mạch dao động \(LC\) lí tưởng được mắc với nguồn điện có suất điện động \(6\;V\), điện trở trong không đáng kể (hình vẽ bên). Điện dung của tụ điện là \(0,5\mu F;\) độ tự cảm của cuộn dây là \(2mH\). Lấy \({\pi ^2} = 10.\) Ban đầu khóa \({\rm{k}}\) ngắt tụ điện chưa tích điện, tại thời điểm \(t = 0\) người ta đóng khóa \({\rm{k}}\) thì trong mạch có dao động điện từ tự do. Kể từ \(t = 0\), thời điểm mà cường độ dòng điện trong mạch có độ lớn \(15\sqrt 3 \pi ({\rm{mA}})\) lần thứ 3 thì điện tích của bản tụ điện nối với khóa \({\rm{k}}\) có giá trị là
- Sóng dừng trên một sợi dây với hai đầu cố định. Khi tần số sóng là \(f\) thì trên sợi dây có 10 nút sóng (kể cả hai đầu). Nếu tần số sóng là \(\frac{4}{3}f\) thì trên dây có số bụng sóng là