YOMEDIA
NONE
  • Câu hỏi:

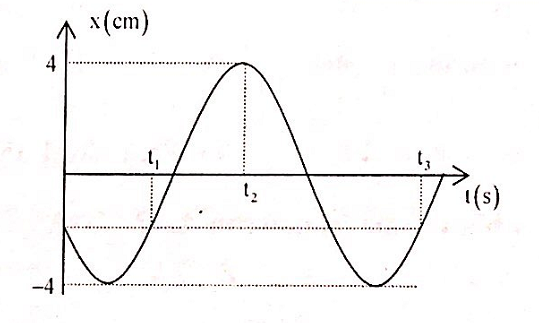
    Một chất điểm DĐĐH. Đồ thị biểu diễn li độ phụ thuộc vào thời gian như hình vẽ. Biết t3 + 2t1 – 3t2 = 0 và tốc độ trung bình của chất điểm từ thời điểm ban đầu đến thời điểm t1 là 6 cm/s. Viết phương trình dao động của chất điểm.

    ​

    • A. \(x = 4\cos \left( {\pi t + \frac{{5\pi }}{6}} \right)\) (cm)
    • B. \(x = 4\cos \left( {\pi t + \frac{{3\pi }}{4}} \right)\) (cm)
    • C. \(x = 4\cos \left( {\pi t - \frac{{2\pi }}{3}} \right)\) (cm)
    • D. \(x = 4\cos \left( {\pi t + \frac{{2\pi }}{3}} \right)\) (cm)

    Lời giải tham khảo:

    Đáp án đúng: D

    + Gọi Δt là thời gian ngắn nhất chất điểm đi từ vị trí ban đầu x0 đến biên âm.

    + Từ đồ thị, ta có:

    \(\left\{ \begin{array}{l}
    {t_1} = 2\Delta t\\
    {t_2} = \frac{T}{2} + \Delta t\\
    {t_3} = T + 2\Delta t
    \end{array} \right.\) 

    + Mặt khác:  

     \(\begin{array}{l}
    {t_3} + 2{t_1} - 3{t_2} = 0\\
     \Leftrightarrow T = 2\Delta t + 4\Delta t - \frac{{3T}}{2} - 3\Delta t = 0 \Rightarrow \Delta t = \frac{T}{6}\\
     \Rightarrow {x_0} =  - \frac{A}{2} =  - 2\left( {{\rm{cm}}} \right) - 2 = 4\cos \varphi \\
     \Rightarrow \varphi  =  \pm \frac{{2\pi }}{3}\varphi  = \frac{{2\pi }}{3}
    \end{array}\)

    + Phương trình:  

    \(\begin{array}{l}
    \overline v  = \frac{{{s_1}}}{{{t_1}}} = \frac{{2 + 2}}{{2.\frac{T}{6}}} \Leftrightarrow 6 = \frac{{12}}{T}\\
     \Rightarrow T = 2\left( s \right) \Rightarrow \omega  = \pi (rad/s)\\
    x = 4\cos \left( {\pi t + \frac{{2\pi }}{3}} \right)cm
    \end{array}\)

    ADSENSE

Mã câu hỏi: 211761

Loại bài: Bài tập

Chủ đề :

Môn học: Vật lý

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài

 
YOMEDIA

Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng

 

 

CÂU HỎI KHÁC

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 12

 

YOMEDIA
AANETWORK
OFF