Hình chiếu vuông góc của điểm S trên mặt phẳng (ABCD) là trung điểm H của AB

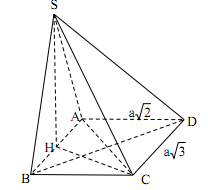
Vì H là hình chiếu của S xuống mp(ABCD) nên \((SC,mp(ABCD)) = (SC,HC) = SCH = {45^0}\)

Xét tam giác BCH vuông tại B, theo định lý Py-ta-go ta có:

\(C{H^2} = B{C^2} + B{H^2} = {\left( {a\sqrt 2 } \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{11{a^2}}}{4}\)

\( \Rightarrow CH = \frac{{a\sqrt {11} }}{2}.\)

Xét tam giác SCH vuông tại H có \(SCH = {45^0} \Rightarrow \Delta SCH\) vuông cân tại H

\( \Rightarrow SH = CH = \frac{{a\sqrt {11} }}{2}\)

Ta có: \({S_{ABCD}} = AB.AD = a\sqrt 3 .a\sqrt 2  = \sqrt 6 {a^2}\)

Do đó: \({V_{S.ABCD}} = \frac{1}{3}.SH.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt {11} }}{2}.{a^2}\sqrt 6  = \frac{{\sqrt {66} {a^3}}}{6}\) (đvtt)