-
Câu hỏi:
Đặt điện áp xoay chiều u=U√2cos(ωt + φ) (V) (với U và ω không đổi) vào hai đầu đoạn mạch AB nối tiếp gồm điện trở thuần R, cuộn dây không thuần cảm (có điện trở r), tụ điện, theo thứ tự đó. Biết R = r. Gọi M là điểm nối giữa R và cuộn dây, N là điểm nối giữa cuộn dây và tụ điện. Đồ thị biểu diễn điện áp uAN và uMB như hình vẽ bên. Giá trị của U gần nhất với giá trị nào sau đây:
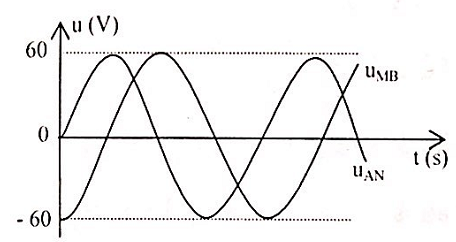
- A. 76 V
- B. 42 V
- C. 85 V
- D. 54 V
Lời giải tham khảo:
Đáp án đúng: D
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
{u_{AN}} = 60\cos \left( {\omega t - \frac{\pi }{2}} \right)\left( V \right)\\
{u_{MB}} = 60\cos \left( {\omega t + \pi } \right)\left( V \right)
\end{array} \right. \Rightarrow {u_{AN}} \bot {u_{MB}}\\
\Rightarrow \tan {\varphi _{AN}}.\tan {\varphi _{MB}} = - 1\\
\Leftrightarrow \frac{{{Z_L}}}{{2R}}.\frac{{{Z_L} - {Z_C}}}{R} = - 1\\
\Leftrightarrow {Z_L}\left( {{Z_C} - {Z_L}} \right) = 2{R^2}
\end{array}\) (1)+ Lại có:
\({U_{AN}} = {U_{MB}} \Leftrightarrow 4{R^2} + Z_L^2 = {R^2} + {\left( {{Z_L} - {Z_C}} \right)^2} \Rightarrow 3{R^2} = Z_C^2 - 2{Z_L}{Z_C}\) (2)
+ Từ (1) và (2), ta có:
\( \Rightarrow \left\{ \begin{array}{l}
{Z_C} = 3{Z_L}\\
{Z_C} = 0,5{Z_L}
\end{array} \right.{Z_C} = 3{Z_L}R = {Z_L} \Rightarrow {Z_C} = 3R\)+ Mặt khác, ta có:
\(\begin{array}{l}
{U_{AN}} = 60 = \frac{{U\sqrt {4{R^2} + Z_L^2} }}{{\sqrt {4{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\
60 = \frac{{{U_0}\sqrt {4{R^2} + {R^2}} }}{{\sqrt {4{R^2} + 4{R^2}} }}\\
\Rightarrow {U_0} = 24\sqrt {10} \Rightarrow U \approx 54\left( V \right)
\end{array}\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Chọn câu trả lời đúng khi nói về dao động điều hòa:
- Số prôtôn và số nơtron trong hạt nhân nguyên từ \(_{30}^{67}Zn\) là:
- Đặt vào hai đầu điện trở R = 100 Ω thì dòng điện trong mạch có biểu thức:
- Một máy biến áp lí tưởng có số vòng dây ở cuộn sơ cấp là N1
- Đặt điện áp xoay chiều u = U0cosωt vào hai đầu một đoạn mạch gồm tụ điện
- Cho đoạn mạch điện xoay chiều không phân nhánh gồm cuộn dây thuần cảm có L = 2/π (H)
- 1 chất điểm dddh có a = 160cos\(\left( {2\pi t + \frac{\pi }{3}} \right)\)
- Khi nói về sóng cơ học, phát biểu nào sau đây là sai
- Một sóng cơ khi truyền theo trục Ox có phương trình là:
- Đại lượng không phải là đặc trưng vật lý của âm?
- Câu nào đúng. Sóng điện từ
- Sóng vô tuyến do đài VOV3 phát ra có tần số 102,7 MHz
- Hiện tượng nhiễu xạ và giao thoa ánh sáng chứng tỏ ánh sáng:
- Chiếu một chùm sáng đơn sắc hẹp tới mặt bên của một lăng kính thủy tinh
- Trong thí nghiệm của Y-âng về giao thoa với ánh sáng đon sắc
- Theo thuyết của Anh-xtanh về lượng tử ánh sáng, phôtôn ứng với mỗi ánh sáng đơn sắc
- Biết công thoát A của electron khỏi một kim loại là 4,14 eV.
- Khi nghiên cứu quang phổ các chất, chất nào khi bị nung nóng nhiệt độ cao
- Chọn câu sai về các tia bức xạ:
- Một dải sóng điện từ có tần số \({4,0.10^{14}}\;Hz - {7,5.10^{14}}\;Hz\)
- Một CLLX gồm một lò xo nhẹ có độ cứng k, vật nặng có khối lượng m = 100g
- Đặt điện áp u =U0cos\(\left( {100\pi t - \frac{\pi }{{12}}} \right)\) (V)
- Độ bền vững của hạt nhân phụ thuộc vào:
- Cho đồ thị biểu diễn li độ của một vật dao động theo thời gian t
- Một máy bay bay ở độ cao 100m, gây ra ở mặt đất ngay phía dưới tiếng ồn
- Trên một phương truyền sóng có hai điểm M và N cách nhau 80cm.
- Hiện nay đèn LED đang có những bước nhảy vọt trong ứng dụng thị trường
- Một người đi xe máy trên đoạn đường cứ 6 m lại có ổ gà
- Một chất phóng xạ có hằng số phóng xạ λ.
- Cho phản ứng hạt nhân \(_2^4He + _7^{14}N \to _1^1H + _Z^AX\).
- Bắn hạt prôtôn với động năng Wp = 1,46MeV vào hạt nhân Li đứng yên
- Trong thí nghiệm giao thoa Y-âng đồng thời với hai ánh sáng đơn sắc
- Một đám nguyên tử hiđrô đang ở trạng thái cơ bản.
- Hiện tượng nào dưới đây nhằm khẳng định ánh sáng có tính chất sóng?
- Trên mặt nước có hai nguồn sóng giống nhau A, B dao dộng cùng pha
- Một con lắc đơn gồm dây treo có chiều dài 1 m
- Đặt điện áp xoay chiều u=U√2cos(ωt + φ) (V) (với U và ω không đổi)
- Ba con lắc lò xo có cùng độ cứng k, dao động điêu hòa cùng phương
- Điện năng được truyền từ nơi phát đến một xưởng sản xuất
- Một mạch dao động LC có điện trở thuần bằng không







