-
Câu hỏi:
Cho mạch điện như hình vẽ. Đặt vào hai đầu A, B một điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Điều chỉnh C để tổng điện áp hiệu dụng UAM + UMB lớn nhất thì tổng đó bằng 2U và khi đó công suất tiêu thụ của đoạn mạch AM là 36 W. Tiếp tục điều chỉnh C để công suất tiêu thụ của đoạn mạch lớn nhất thì công suất lớn nhất đó bằng
.png)
- A. 32 W.
- B. 36 W.
- C. 25 W.
- D. 48 W.
Lời giải tham khảo:
Đáp án đúng: D
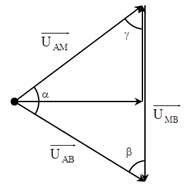
+ Biểu diễn vecto các điện áp.
+ Áp dụng định lý sin trong tam giác, ta có:
\(\frac{{{U}_{AM}}}{\sin \beta }=\frac{{{U}_{MB}}}{\sin \alpha }=\frac{{{U}_{AB}}}{\sin \gamma }=\frac{{{U}_{AM}}+{{U}_{MB}}}{\sin \alpha +\sin \beta }\to {{U}_{AM}}+{{U}_{MB}}=\frac{{{U}_{AB}}}{\sin \gamma }\left( \sin \alpha +\sin \beta \right)\)
với \(\gamma \) luôn không đổi.
\({{U}_{AM}}+{{U}_{MB}}=\frac{2{{U}_{AB}}}{\sin \gamma }\sin \left( \frac{\alpha +\beta }{2} \right)\cos \left( \frac{\alpha -\beta }{2} \right)=\frac{2{{U}_{AB}}}{\sin \gamma }\sin \left( \frac{180-\gamma }{2} \right)c\text{os}\left( \frac{\alpha \text{-}\beta }{\text{2}} \right)\)
\(\to {{\left( {{U}_{AM}}+{{U}_{MB}} \right)}_{\max }}\) khi \(\alpha =\beta .\)
=> \({{\left( {{U}_{AM}}+{{U}_{MB}} \right)}_{\max }}=\frac{2U}{\sin \gamma }\sin \left( \frac{180-\gamma }{2} \right)=2U\to \gamma =60{}^\circ .\)
\(\to \) Các vecto hợp với nhau thành tam giác đều \(\to \) khi xảy ra cực đại u chậm pha hơn i một góc \(30{}^\circ \).
\(P={{P}_{\max }}{{\cos }^{2}}\varphi \to {{P}_{\max }}=\frac{P}{{{\cos }^{2}}\varphi }=\frac{36}{{{\cos }^{2}}30{}^\circ }=48\,\,W.\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Nếu chiếu một chùm tia hồng ngoại vào tấm kẽm tích điện âm
- Trong trường hợp nào sau đây ta có thể coi các vật nhiễm điện
- Trường hợp nào sao đây là biểu hiện của “ từ trường “ ?
- Trong quá trình truyền tải điện năng biện pháp giảm hao phí trên đường dây
- Sóng (cơ học) ngang:
- Trong các ánh sáng đơn sắc sau đây.
- Hạt nhân \({}_{92}^{238}U\) có cấu tạo
- Phát biểu nào sau đây là đúng khi nói về phản ứng hạt nhân?
- Một vật dao động điểu hòa khi đang chuyển động từ vị trí cân bằng
- Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là
- Một vật nhỏ dao động điều hòa theo một trục cố định.
- Kim loại làm catốt của một tế bào quang điện có giới hạn quang điện là λo.
- Tốc độ truyền âm trong không khí là 340m/s
- Khi một hạt nhân nguyên tử phóng xạ lần lượt một tia α và một tia β–
- Đặt vào hai đầu đoạn mạch RLC nối tiếp một hiệu điện thế xoay chiều
- Lần lượt chiếu hai bức xạ có bước sóng λ1 = 0,75 μm và λ2 = 0,25 μm
- Một đoạn mạch xoay chiều gồm cuộn dây thuần cảm L = 1/p (H)
- Có 100 (g) chất phóng xạ với chu kì bán rã là 7 ngày đêm.
- Cho ba điện tích q1= 4µC, q2= 16µC, q3 = - 64µC
- Cho một mạch điện có suất điện động của bộ nguồn ξ=30V .
- Đặt vào hai đầu mạch điện chỉ có cuộn thuần cảm một điện áp xoay chiều
- Trên vỏ của một acquy có ghi 12V, điện trở trong của acquy là 0,06
- Dòng điện trong cuộn tự cảm giảm từ 16A đến 0A trong thời gian 0,01s.
- Một người mắt có tật phải đeo kính có độ tụ - 4dp mới thấy rõ các vật ở xa
- Trong thí nghiệm về sóng dừng, trên một sợi dây đàn hồi dài 1,2m
- Một sóng ngang có chu kì T = 0,2 s truyền trong một môi trường đàn hồi
- Tại hai điểm A và B trên mặt nước cách nhau 16 cm có hai nguồn giống nhau.
- Trong một mạch dao động LC không có điện trở thuần, có dao động điện từ tự do.
- Một mạch chọn sóng của máy thu có cuộn cảm L=2mH
- Hai sóng cùng tần số, được gọi là sóng kết hợp, nếu có
- Quang phổ Mặt Trời được máy quang phổ ghi được là:
- Trong thí nghiệm Y-âng, hai khe được chiếu bằng ánh sáng trắng
- Trong thí nghiệm giao thoa ánh sáng với khe Y âng, khoảng cách giữa hai khe
- Đặt điện áp u = U0cos100πtV vào hai đầu đoạn mạch A, B
- Hai dao động điều hòa có đồ thị li độ - thời gian như hình
- Một con lắc lò xo nằm ngang gồm vật nặng M = 200 g
- Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn S phát ra ba ánh sáng
- Cho mạch điện như hình vẽ sau:
- Tia tử ngoại không có tác dụng nào say đây?
- Điện năng từ nhà máy được đưa tới nơi tiêu thụ nhờ các dây dẫn.







